-
1、下列各数中,哪些是有理数,哪些是无理数?
- , 3.9 , -234.10101010…(相邻两个1之间有1个0),0.12345678910111213…(小数部分由相继的正整数组成).
-
2、 a是一个实数,它的相反数和绝对值如何表示?若 则它的倒数如何表示?
-
3、 比较-3.14与-π的大小.
-
4、下列各数中,哪些是有理数,哪些是无理数?
0.4583, 3. , - π,- , 18.
-
5、下列各数中,哪些是有理数,哪些是无理数?
3.14,- , 0. , 0.1010001000001…(相邻两个1之间0的个数逐次加2).
-
6、如图,等边三角形ABC的边长为2,高为h,h可能是有理数吗?

-
7、归纳是数学发现的重要方法,但仅仅由几种特殊情况归纳出来的结论并不可靠.请你查阅资料,了解数学史上有关这方面的一些事例,并在班级内分享.
-
8、 如图,AB∥DE,BC∥EF, 你能判断∠ABC与的大小关系吗?小颖据此得出结论:如果两个角的两边分别平行,那么这两个角相等.你认为她的判断正确吗?

-
9、观察下列各式:
.
你能否得到结论“所有奇数都可以表示为两个自然数的平方差”?所有偶数呢?请说明理由.
-
10、八(1)班有39名同学,他们每人将自己的学号作为n的取值( 3,…,39)代入式子 结果发现式子 的值都是质数,于是他们猜想:对于所有的自然数,式子 的值都是质数.
你认为这个猜想正确吗?
-
11、 当n为正整数时, 的值一定是质数吗?
-
12、
 (1)、图(1)中有三条线段a,b,c,哪一条和线段d在同一条直线上?请你先观察,再用直尺验证一下.(2)、图(2)中两条线段a与b的长度相等吗?
(1)、图(1)中有三条线段a,b,c,哪一条和线段d在同一条直线上?请你先观察,再用直尺验证一下.(2)、图(2)中两条线段a与b的长度相等吗? -
13、新定义:若两个角的和为100°,我们则称这两个角互为“百度角”;例如°,°,则与互为“百度角”.(本题中所研究的角都是大于0°而小于180°的角.)
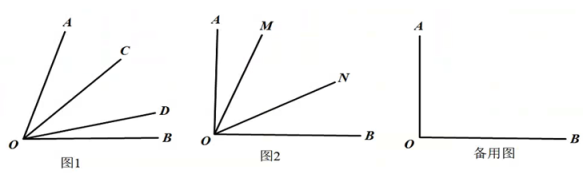 (1)、【阅读理解】
(1)、【阅读理解】如图1,如果°,与互为“百度角”,则= .
(2)、【初步应用】射线平分角 , 为内部的一条射线且满足°,若与互为“百度角”,求的值.
(3)、【解决问题】如图2,已知°,射线从出发,以每秒10°的速度绕点顺时针旋转,同时,射线从出发,以每秒5°的速度绕点逆时针旋转,设运动的时间为秒(0<t<18).当为何值时由三条射线形成的角中有两个角互为“百度角”?
-
14、如图一张规格为6dm×8dm的大纸板有两种剪裁方式分别可得到型长方形纸板和型正方形纸板,再制作成横式和竖式两种无盖长方体纸盒(盖在上方).已知一张大纸板可以恰好裁成8张型长方形纸板或者恰好裁成12张型正方形纸板.
 (1)、制作一个横式纸盒需要A型长方形纸板张,制作一个竖式纸盒需要A型长方形纸板张.(2)、若用7张大纸板裁成型长方形纸板,用2张大纸板剪裁型正方形纸板,且裁成的两种型号纸板恰好都用完,求可以制作横式纸盒和竖式纸盒各多少个?(3)、如果制作横式纸盒和竖式纸盒均为个,若可用于剪裁的大纸板不超过18张,求的最大值.
(1)、制作一个横式纸盒需要A型长方形纸板张,制作一个竖式纸盒需要A型长方形纸板张.(2)、若用7张大纸板裁成型长方形纸板,用2张大纸板剪裁型正方形纸板,且裁成的两种型号纸板恰好都用完,求可以制作横式纸盒和竖式纸盒各多少个?(3)、如果制作横式纸盒和竖式纸盒均为个,若可用于剪裁的大纸板不超过18张,求的最大值. -
15、如图,在中,点在边上,连接 , , 是中边上的高线,延长交于点 , 设 , .
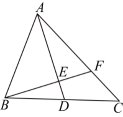 (1)、当=65°时,的度数为;(2)、求的度数(用含的式子表示);(3)、若 , 求的值.
(1)、当=65°时,的度数为;(2)、求的度数(用含的式子表示);(3)、若 , 求的值. -
16、已知关于、的方程组 .(1)、求方程组的解(用含的代数式表示);(2)、若方程组的解满足条件 , 且 . 求的取值范围.
-
17、如图,11×13方格图中每个小正方形的边长都为1,是由向右平移4格,再向上平移2格得到的.利用方格点和直尺画图、填空.
 (1)、请在图中画出;(2)、将绕点顺时针旋转90°得到△A''BC'',画出旋转后的图形;(3)、在图中能使的格点的个数有个.(格点是指方格图中横向和纵向线条的交点)
(1)、请在图中画出;(2)、将绕点顺时针旋转90°得到△A''BC'',画出旋转后的图形;(3)、在图中能使的格点的个数有个.(格点是指方格图中横向和纵向线条的交点) -
18、解不等式组 , 并把解集在数轴上表示出来.
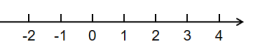
-
19、解下列方程或方程组(1)、(2)、
-
20、定义一种新运算“※”,规定 , 其中 , 为常数,且 , , 则 .