相关试卷

1、计算： $- 3^{2} \div \frac{3}{4} \times (- \frac{1}{2}) - [1 + {(- 2)}^{3}] - |- 6|$ ．

查看解析
2、化简： $9 a - 4 a + 3 b - 5 a - 2 b$ ；

查看解析
3、已知一个直棱柱共有10个顶点，它的底面边长都是 $4 cm$ ，侧棱长都是 $5 cm$ ，则它的侧面积（） ${cm}^{2}$ ．

A、120 B、100 C、80 D、20

查看解析
4、用一个平面去截三棱柱，截面不可能是（）

A、三角形 B、矩形 C、五边形 D、六边形

查看解析
5、规定：不相交的两个函数图象在竖直方向上的最短距离为这两个函数的“亲近距离”
（1）求抛物线y＝x²﹣2x+3与x轴的“亲近距离”；
（2）在探究问题：求抛物线y＝x²﹣2x+3与直线y＝x﹣1的“亲近距离”的过程中，有人提出：过抛物线的顶点向x轴作垂线与直线相交，则该问题的“亲近距离”一定是抛物线顶点与交点之间的距离，你同意他的看法吗？请说明理由．
（3）若抛物线y＝x²﹣2x+3与抛物线y＝ $\frac{1}{4} x^{2}$ +c的“亲近距离”为 $\frac{2}{3}$ ，求c的值．

查看解析
6、如图，点C在△ADE的边DE上，AD与BC相交于点F，∠1=∠2， $\frac{A B}{A C} = \frac{A D}{A E}$ ．
（1）试说明：△ABC ∽△ADE；
（2）试说明：AF•DF=BF•CF．

查看解析
7、如图，一次函数 $y_{1} = - x + 5$ 与反比例函数 $y_{2} = \frac{k}{x}$ 的图像交于A（1，m）、B（4，n）两点．
（1）求A、B两点的坐标和反比例函数的解析式；
（2）根据图像，直接写出当 $y_{1} > y_{2}$ 时x的取值范围．

查看解析
8、某数学兴趣小组想用所学的知识测量小河的宽．测量时，他们选择了河对岸的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得 $A B$ 与河岸垂直，并在B点竖起标杆 $B C$ ，再在 $A B$ 的延长线上选择点D，竖起标杆 $D E$ ，使得点E，C，A共线．已知： $C B ⊥ A D$ ， $E D ⊥ A D$ ，测得 $B C = 1 m$ ， $D E = 1.5 m$ ， $B D = 7 m$ （测量示意图如图所示）．请根据相关测量信息，求河宽 $A B$ 的长．

查看解析
9、如图，在平行四边形 $A B C D$ 中， $A C$ ， $B D$ 相交于点O，点E是 $O A$ 的中点，连接 $B E$ 并延长交 $A D$ 于点F．已知 $S_{△ A E F} = 4$ ，则下列结论：① $\frac{A F}{F D} = \frac{1}{2}$ ；② $S_{△ B C E} = 36$ ， ③ $S_{△ A B E} = 12$ ；④ $△ A E F ∽ △ A C D$ ，其中一定正确的是（填序号）．

查看解析
10、若 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{1}{2}$ ， $3 b - 2 d + f \neq 0$ ，则 $\frac{3 a - 2 c + e}{3 b - 2 d + f}$ = ．

查看解析
11、下列各线段的长度成比例的是（）

A、2cm，5cm，6cm，8cm B、1cm，2cm，3cm，4cm C、3cm，6cm，7cm，9cm D、3cm，6cm，9cm，18cm

查看解析
12、“一盔一带”是公安部在全国开展的一项安全守护行动，也是营造文明城市，做文明市民的重要标准，“一盔”是指安全头盔，电动自行车驾驶人和乘坐人员应当佩戴安全头盔．某商场欲购进一批安全头盔，已知购进3个甲种型号头盔和2个乙种型号头盔需要220元，购进1个甲种型号头盔和5个乙种型号头盔需要290元．

(1)、甲、乙两种型号头盔的进货单价分别是多少？

(2)、若该商场计划购进甲、乙两种型号头盔共200个，且乙种型号头盔的购进数量最多为90个．已知甲种型号头盔每个售价为55元，乙种型号头盔每个售价为75元．若该商场将这两种型号头盔全部售出可获利W元，则应该如何进货才能使该商场获利最大？最大利润是多少元？

查看解析
13、【问题背景】小李同学在学习了数学第13章内容后，他对三角形的三边关系及三角形的中线特别感兴趣，下面是他总结的一些题目笔记．请同学们帮他分析．
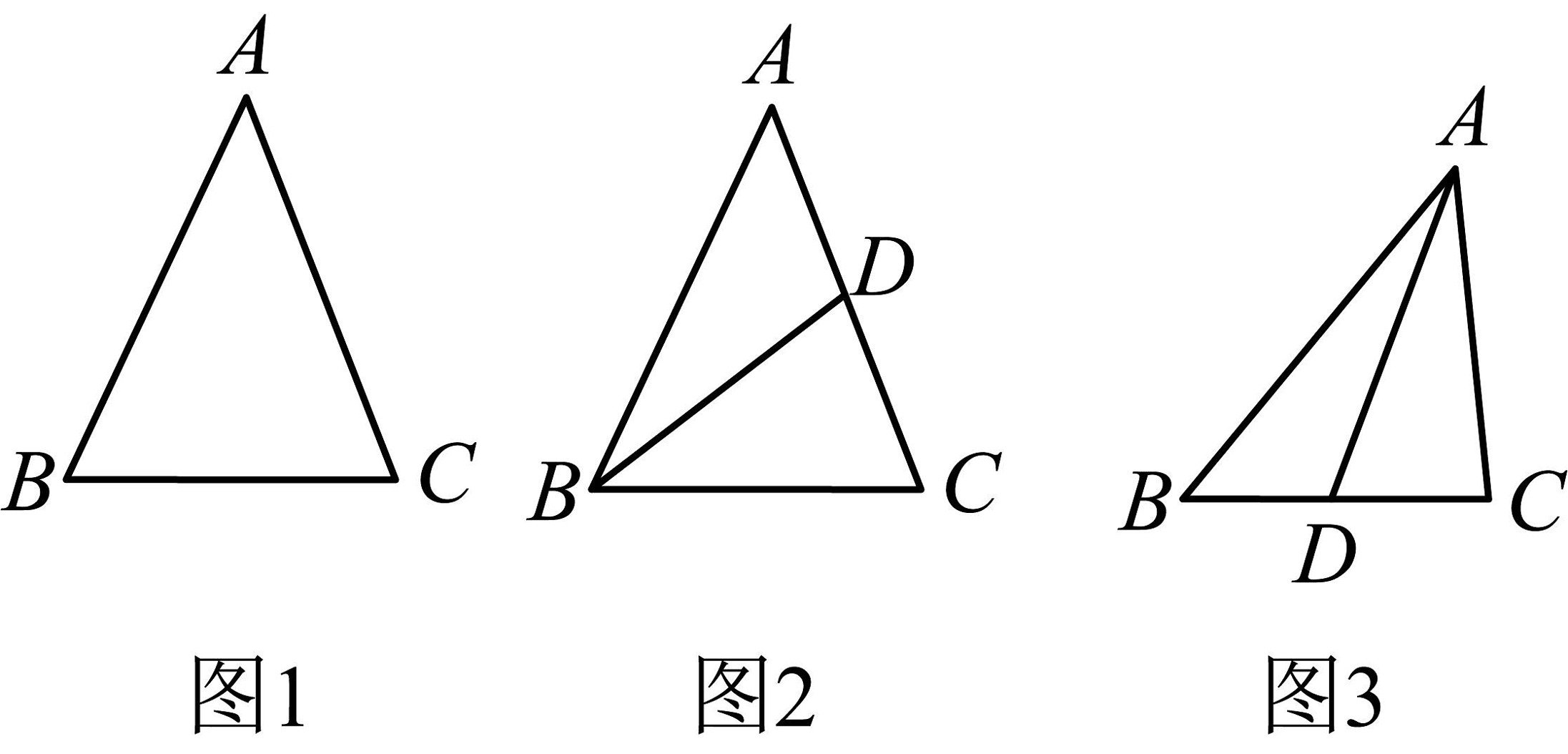
【新知探究】如图1，在等腰 $△ A B C$ 中， $A B$ 、 $A C$ 是 $△ A B C$ 的腰．已知三角形两条边的长度分别为 $4cm$ ， $9cm$ ，求 $△ A B C$ 的周长？小李经过计算，得出的 $△ A B C$ 的周长是 $17cm$ 或 $22cm$ ．
任务1：小李的答案是否正确？如果不正确请写出正确的答案．
【新知拓展】根据【任务1】的答案，小李继续探索三角形中线的重要作用．
如图2，当添加条件： $B D$ 是等腰 $△ A B C$ 的中线时．求 $△ A B D$ 与 $△ C B D$ 的周长差．
任务2：请你帮小李写出解答过程．
【拓展应用】结合【任务2】的解答过程，小李继续探索三角形中线在一般三角形中是否具有同样作用．
如图3，在 $△ A B C$ 中，已知 $A D$ 是 $△ A B C$ 的中线（且 $A B > A C$ ），其中 $A B = m$ ， $A C = n$ ．则 $△ A B D$ 与 $△ A C D$ 的周长差是多少．
任务3：请用含 $m$ ， $n$ 的代数式表示 $△ A B D$ 与 $△ A C D$ 的周长差．

查看解析
14、如图，在平面直角坐标系中直线m： $y = k x + b$ 与直线n： $y = 2 x + 8$ 交于点 $A (- 1, 6)$ ，直线m、n分别与x轴交于点B、C，其中点 $B (2, 0)$ ．

(1)、求直线m对应的函数表达式；

(2)、求 $△ A B C$ 的面积；

(3)、直接写出不等式 $k x + b \geq 2 x + 8$ 的解集．

查看解析
15、如图，在 $△ A B C$ 中， $∠ A = 40 °$ ， $∠ A B D = 32 °$ ， $B D$ 是 $△ A B C$ 的角平分线， $C E$ 是 $△ B C D$ 的角平分线．求 $∠ C E D$ 的度数．

查看解析
16、已知点 $P (3 a + 1, a - 5)$ ，解答下列各题．

(1)、点P在x轴上，求点P的坐标；

(2)、点Q的坐标为 $(- 2, 3)$ ，直线 $P Q ∥ y$ 轴，求点P的坐标．

查看解析
17、观察以下图形，猜测第 $n$ 个图形中有个三角形（用含 $n$ 的代数式表示结论）

查看解析
18、等腰三角形有一个角的度数为 $50 °$ ，则它一条腰上的高与另一条腰的夹角的度数是．

查看解析
19、直线 $y = - 3 x + 2$ 经过点 $P (a ， b)$ ，则 $6 a + 2 b + 2024$ 的值为．

查看解析
20、若点 $A (- 1, y_{1})$ 和点 $B (3, y_{2})$ 在一次函数 $y = 4 x - 1$ 的图象上，则 $y_{1}$ $y_{2}$ （用“>”、“<”或“=”连接）．

查看解析

上一页 194 195 196 197 198 下一页跳转