相关试卷
-
1、2024年5月28日,神舟十八号航天员叶光富、李聪、李广苏密切协同,完成出舱活动,活动时长约 , 刷新了中国航天员单次出舱活动时间纪录,进一步激发了青少年热爱科学的热情.某校为了普及“航空航天”知识,从该校1200名学生中随机抽取了部分学生参加“航空航天”知识测试,并将测试成绩(百分制)整理绘制成如下不完整的统计图表:
成绩统计表
组别
成绩/分
百分比
A组
B组
C组
D组
E组
成绩条形统计图

根据所给信息,解答下列问题:
(1)、本次调查的成绩统计表中 , 并补全条形统计图;(2)、被抽取的学生成绩的中位数落在组(填A , B , C , D或E);(3)、试估计该校1200名学生中成绩在80分以上(包括80分)的人数. -
2、如图,在四边形中,是的中点,、交于点 , , .
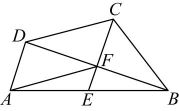 (1)、求证:四边形为平行四边形;(2)、若 , , , 求的长.
(1)、求证:四边形为平行四边形;(2)、若 , , , 求的长. -
3、解方程:(1)、(2)、
-
4、计算:
-
5、如图,在中, , , , 点、分别在线段、上,且 , 连结 , 若平分 , 则的长为 .
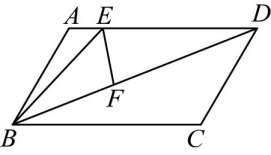
-
6、在平面直角坐标系中,一副三角尺如图放置, , 点在轴的正半轴上,点、在反比例函数的图象上.若轴, , 则的值为 .
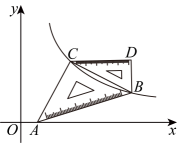
-
7、某网店某种商品成本为50元/件,售价为60元/件时,每天可销售100件;售价单价高于60元时,每涨价1元,日销售量就减少2件.据此,当销售单价为元时,网店该商品每天盈利最多.
-
8、若点与点关于坐标原点对称,则的值为 .
-
9、已知一样本数据4,4,5,6,的平均数为5,则数的值为 .
-
10、一个正多边形的每个外角都等于 , 那么它是边形.
-
11、如图,在正方形中,对角线、交于点 , 延长到 , 连结 , 过点作 , 分别交、于点、 , 连结 , 则下面哪个图形的面积与的面积相等( )
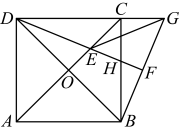 A、四边形 B、 C、四边形 D、
A、四边形 B、 C、四边形 D、 -
12、反比例函数的图像上有 , 两点,下列判断正确的是( )A、当时, B、当且时, C、当时, D、当且时,
-
13、在菱形中, , 点、分别在边、上,连结、 , 则添加下列条件后,不能判定的是( )A、 B、 C、 D、
-
14、若关于的一元二次方程有两个相等的实数根,则的值是( )A、 B、 C、 D、
-
15、用反证法证明:“在中,对边分别是a、b . 若 , 则 . ”第一步应假设( )A、 B、 C、 D、
-
16、某校九年级进行了三次数学模拟考试,甲、乙、丙三名同学的平均分和方差如表所示,则这三名同学中数学成绩最稳定的是( )
统计量
甲
乙
丙
93
93
93
14
18
11
A、甲 B、乙 C、丙 D、无法确定 -
17、将函数的图像向右平移3个单位,所得的二次函数解析式是( )A、 B、 C、 D、
-
18、二次根式中字母的取值范围是( )A、 B、 C、 D、
-
19、下列标志中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
20、正方形中,点E为上一动点(不与端点重合),连接 , 过点B作于点F,过点D作于点G.
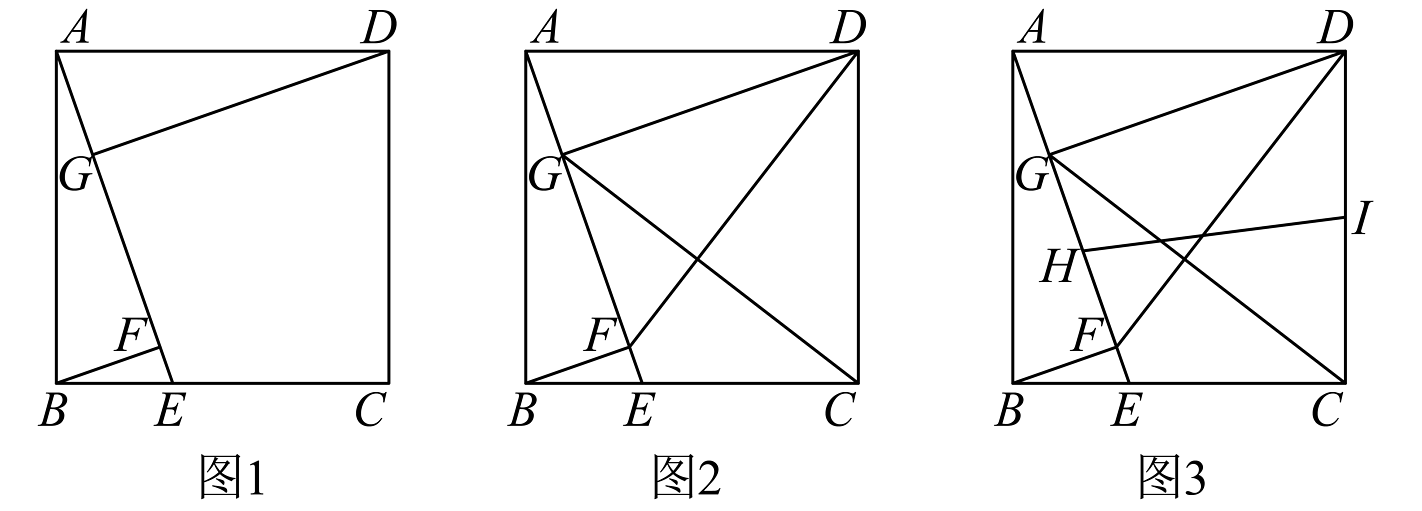 (1)、如图1,若 , , 求的长度;(2)、如图2,连结 , , 判断和的数量关系,并说明理由;(3)、如图3,点H,I分别为 , 中点,连接;判断和的数量关系,并说明理由.
(1)、如图1,若 , , 求的长度;(2)、如图2,连结 , , 判断和的数量关系,并说明理由;(3)、如图3,点H,I分别为 , 中点,连接;判断和的数量关系,并说明理由.