相关试卷
-
1、下列式子正确的是( )A、 B、 C、 D、
-
2、正多面体是指各个面都是全等的正多边形,并且各个多面角都是全等的多面角,又称为柏拉图多面体,因为柏拉图及其追随者对它们所作的研究而得名,自然界中有许多的柏拉图多面体,如甲烷、金刚石分子结构模型都是正四面体,氯化钠的分子结构模型是正六面体,萤石的结晶体有时是正八面体,硫化体的结晶体有时会接近正十二面体的形状.....柏拉图多面体满足性质:V+F-E=2(其中V,F和E分别表示多面体的顶点数,面数和棱数)。
 (1)、正十二面体共有几条棱,几个顶点?(2)、如图所示的正方体中,点G,H,I,J,K,L为正方体六个面的中心,假设几何体GHIJKL的体积为 , 正方体的体积为 , 求的值;(3)、判断柏拉图多面体有多少种?并说明理由,
(1)、正十二面体共有几条棱,几个顶点?(2)、如图所示的正方体中,点G,H,I,J,K,L为正方体六个面的中心,假设几何体GHIJKL的体积为 , 正方体的体积为 , 求的值;(3)、判断柏拉图多面体有多少种?并说明理由, -
3、记的内角的对边分别为a,b,c,已知 .(1)、若 , 证明:;(2)、若 , 证明: .
-
4、某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为x,y(i=1,2…,10).试验结果如下:
试验序号i
1
2
3
4
5
6
7
8
9
10
伸缩率х1
545
533
551
522
574
544
541
568
596
536
伸缩率у1
536
527
543
530
560
533
522
550
576
536
记 , 记的样本平均数为 , 样本方差为 .
(1)、求;(2)、判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果 , 则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高) -
5、已知向量 , , .(1)、若 , 求x的值;(2)、记 , 求函数的最大值和最小值及对应的x的值.
-
6、在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是.
-
7、某老年健康活动中心随机抽取了6位老年人的收缩压数据,分别为120,96,153,146,112,136,则这组数据的40%分位数为.
-
8、如图,已知直线 , 点A是 , 之间的一个定点,点A到 , 的距离分别为1,2.点B是直线上一个动点,过点A作 , 交直线l_1于点C, , 则( )
 A、 B、面积的最小值是 C、 D、存在最小值
A、 B、面积的最小值是 C、 D、存在最小值 -
9、过所在平面外一点P,作 , 垂足为O,连接PA、PB、PC,则下列说法正确的是( )A、若 , 则点O是的外心 B、若 , , 则点O是AB边的中点 C、若 , , , 垂足都为P,则点O是的垂心 D、若P到三条边的距离相等,则点O是的重心
-
10、已知函数的定义域为R, , 则( ).A、 B、 C、是偶函数 D、是奇函数
-
11、在空间中,过点A作平面的垂线,垂足为B,记.设 , 是两个不同的平面,对空间任意一点P, , , 恒有 , 则( )A、平面\alpha与平面\beta垂直 B、平面与平面所成的(锐)二面角为 C、平面与平面平行 D、平面与平面所成的(锐)二面角为
-
12、有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7’,则( )A、甲与丙相互独立 B、甲与丁相互独立 C、乙与丙相互独立 D、丙与丁相互独立
-
13、函数在区间[-2.8,2.8]的图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
14、已知某4个数据的平均数为6,方差为3,现又加入一个数据6,此时这5个数据的方差为( )A、 B、 C、 D、
-
15、设 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、
-
16、设 , 是向量,则“”是“或”的( ).A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
17、如图1,已知正方形的边长为 , 点是正方形内一动点,且 , 连结、、 , 并延长交于 .
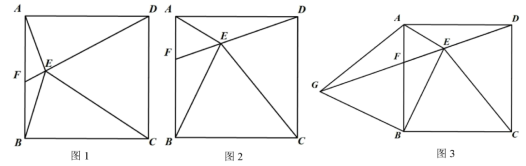 (1)、求证:;(2)、若时,
(1)、求证:;(2)、若时,①如图2,求的长度;
②如图3,延长至点 , 使得 , 连结 . 求与四边形的面积比;
(3)、在图1中,在运动过程中,当的值最小时,求的长.(直接写出答案) -
18、已知抛物线( , 为常数)经过点 , .(1)、求抛物线的函数表达式;(2)、当时, , 当时, , 且 , 为两个连续偶数,求的值;(3)、该抛物线与直线(为常数且)相交于 , 两点,且在的左侧.若在范围内,的取值恰好有3个整数值,求的取值范围.
-
19、如图,学校为美化环境,准备用总长为的篱笆,在靠墙的一侧设计一块矩形花圃 , 其中墙长 , 花圃三边外围用篱笆围起,并在边上留一个宽的门(建在处,另用其他材料).
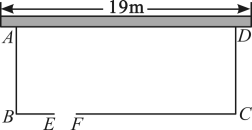 (1)、若花圃的面积为 , 求花圃的一边的长;(2)、花圃的面积能达到吗?如果能,请你给出设计方案,如果不能,请说明理由.
(1)、若花圃的面积为 , 求花圃的一边的长;(2)、花圃的面积能达到吗?如果能,请你给出设计方案,如果不能,请说明理由. -
20、如图,一次函数与反比例函数的图像交于点 , .
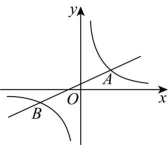 (1)、求的值和一次函数的表达式;(2)、根据函数图象,直接写出不等式的解集.
(1)、求的值和一次函数的表达式;(2)、根据函数图象,直接写出不等式的解集.