相关试卷
-
1、 一个正方形的面积是11,估计它的边长大小在( )A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间
-
2、 在实数(每两个1之间0的个数依次增加1)中,无理数有( )A、1个 B、2个 C、3个 D、4个
-
3、 下列方程组中,解为的是( )A、 B、 C、 D、
-
4、 已知 , 下列不等式变形中正确的是( )A、 B、 C、 D、
-
5、 下列各图中,与是对顶角的是( )A、
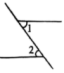 B、
B、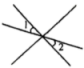 C、
C、 D、
D、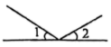
-
6、已知关于x,y的方程组 的解满足x+y<0,x-y>0,则m的取值范围为.
-
7、若关于x,y的二元一次方程组 的解中x是非负数,y的值不大于-1,则a的取值范围为.
-
8、已知关于x的不等式组 的整数解是-1,0,1,2,确定字母a的取值范围.
-
9、若关于x的一元一次不等式组 至少有2个整数解,则a的取值范围是.
-
10、若关于x的不等式组 有且只有3个整数解,则a的取值范围在数轴上表示为( )A、
 B、
B、 C、
C、 D、
D、
-
11、若关于x的不等式组 无解,则a的取值范围是( )A、a<-2 B、a≤-2 C、a>-2 D、a≥-2
-
12、若关于x的一元一次不等式组 有解,则a的取值范围是( )A、a≥4 B、a>4 C、a≤4 D、a<4
-
13、关于x的不等式组 的解集中,任意一个x 的值均在3≤x<7的范围内,则a的取值范围为.
-
14、若关于x的不等式组 的解集为x>5,则m的取值范围为.
-
15、已知关于x的不等式2x≥a-1 的解集是 x≥-1,则 a 的值是
-
16、如图,AD 为△ABC 的角7平分线,点E,F分别在AB,AC上,AE=AF,连结DE,DF,请判断线段AD 所在直线是否为线段EF 的垂直平分线,如果是,给予证明;如果不是,请说明理由.

-
17、如图,在四边形 ABCD 中,AD=CD,AB=CB,我们把这种两组邻边分别相等的四边形叫作“筝形”,有下列结论:①AE=CE;②BD⊥AC;③四边形 ABCD 的面积为 AC·BD.其中正确的有( )
 A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个 -
18、小明在学习等腰三角形的相关知识时,发现其性质定理“等边对等角”与判定定理“等角对等边”存在互逆关系.
由此,爱动脑的小明进行了如下思考:“等腰三角形三线合一”的性质可以分解为多个不同的真命题,即:
⑴等腰三角形顶角的平分线也是底边上的高线;
⑵等腰三角形底边上的中线也是底边上的高线;
⑶……
由这些真命题,小明得到“互逆”之后的新命题,即:
Ⅰ.如果一个三角形一个角的平分线也是这个角对边上的高线,那么这个三角形是等腰三角形;
Ⅱ…
(1)、请你根据前面的命题(2)写出小明猜想的命题Ⅱ:;(2)、小明认为如果这些命题是真命题,那么就可以作为等腰三角形的判定方法,于是小明对命题进行证明,他把第一个命题根据图(1)写出了已知、求证.
命题Ⅰ:已知:在△ABC 中,AD 平分∠BAC,AD⊥BC.求证:△ABC 是等腰三角形.
命题Ⅱ: ▲ .
①请你根据图(2)写出命题Ⅱ的几何语言;
②命题Ⅰ、Ⅱ是否都为真命题?如果不是,请说明理由;如果是,请帮助小明进行证明.
-
19、命题“如果a=1,那么|a|=1”的逆命题为.
-
20、下列定理没有逆定理的是( )A、两直线平行,内错角相等 B、全等三角形的对应角相等 C、等边三角形的三边相等 D、等腰三角形两底角相等