相关试卷
-
1、若实数 , 满足则的值为 .
-
2、如图, , 为上一点, , 且平分 , 过点作于点 , 且 , 则下列结论:①;②;③平分;④平分 . 其中正确结论的序号是( )
 A、①②③ B、①② C、①③ D、②④
A、①②③ B、①② C、①③ D、②④ -
3、如图,将沿方向平移到的位置,量得 , 则间的距离是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、下列四个数中,为不等式组的解的是( )A、 B、0 C、1 D、2
-
5、下列说法不正确的是( )A、点在第二象限 B、点到轴的距离为2 C、若中 , 则点在轴上 D、若在轴上,则
-
6、下列四个数中,最小的数是( )A、 B、0 C、1 D、
-
7、对于不等式4x+7(x-2)>8,不是它的解的是( )A、5 B、4 C、3 D、2
-
8、下列各方程中,是二元一次方程的是( )A、 B、 C、 D、
-
9、下列调查中,适宜采用全面调查(普查)方式的是( )A、了解全国中学生的用眼卫生情况 B、对冷饮市场上冰淇淋质量情况的调查 C、对格力空调的市场占有率的调查 D、对我国首架大型民用直升机各零部件的检查
-
10、如图,在平面直角坐标系中,点 , , 且 , 是的立方根.
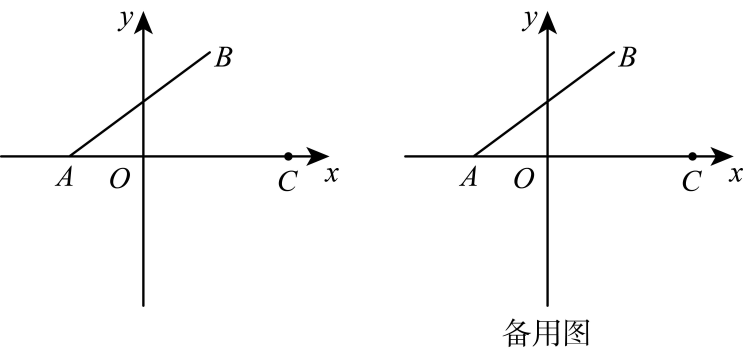 (1)、直接写出: , , ;(2)、将线段平移得到线段 , 点的对应点是点 , 点的对应点是点 .
(1)、直接写出: , , ;(2)、将线段平移得到线段 , 点的对应点是点 , 点的对应点是点 .①在平面直角坐标系中画出平移后的线段 , 直接写出点的坐标;
②若点在轴上,且三角形的面积是 , 求点的坐标;
(3)、在(2)的条件下,点在轴负半轴上运动,但不与点重合,直接写出、、之间的数量关系. -
11、襄阳市某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查,这两种蔬菜的进价和售价如下表所示.
有机蔬菜种类
进价/(元)
售价/(元)
甲
m
16
乙
n
18
(1)、该超市购进甲种蔬菜和乙种蔬菜需要170元;购进甲种蔬菜和乙种蔬菜需要200元.求m , n的值;(2)、该超市决定每天购进甲、乙两种蔬菜共进行销售,其中甲种蔬菜的数量不少于 , 且不大于 , 实际销售时,由于多种因素的影响,甲种蔬菜超过的部分,当天需要打5折才能售完,乙种蔬菜能按售价卖完,求超市当天售完这两种蔬菜获得的利润额y(元)与购进甲种蔬菜的数量之间的函数关系式,并写出x的取值范围;(3)、在(2)的条件下,该超市如何购买花菜才能使当天的利润最大? -
12、如图1, , 的平分线交于点G , .
 (1)、试说明:;(2)、如图2,线段上有点P , 满足 , 过点C作 .
(1)、试说明:;(2)、如图2,线段上有点P , 满足 , 过点C作 .①若在直线上取一点M , 使 , 求的值.
②若 , 将绕点B旋转 , 当为何值时,的一边与平行,请直接写出的值.
-
13、如图,三角形在网格图中,已知点 , .
 (1)、在图中建立平面直角坐标系;(2)、将三角形平移,使点平移到点的位置,点平移后的对应点分别为 , , 画出三角形;(3)、若点是三角形边上一点,经过第(2)问中的平移后,点对应的点的坐标是 .
(1)、在图中建立平面直角坐标系;(2)、将三角形平移,使点平移到点的位置,点平移后的对应点分别为 , , 画出三角形;(3)、若点是三角形边上一点,经过第(2)问中的平移后,点对应的点的坐标是 . -
14、为了解本校初三年级男生排球训练情况,学校体育组在训练之初,随机抽取部分男生进行排球“对墙垫球”测试,记“一分钟对墙垫球次数”为排球测试成绩,对所抽取男生的排球测试成绩分组统计,制成如下统计表1.经过一段时间训练后,再次抽查这部分男生一分钟对墙垫球次数,测试成绩制成如图所示的频数分布直方图.
表1 训练之初被抽样男生测式成绩统计表
组别
成绩
频数
百分比
8
13
10
8

若男生“对墙垫球”23次以上(含23次)记为达标,33次以上(含33次)记为满分.根据以上图表信息,回答下列问题:
(1)、写出 , 的值: , ;(2)、若该校初三年共840人,男女比例为 . 试估计训练后,全年段男生达标人数有多少人?(3)、请你评价男生排球的训练效果. -
15、(1)、解方程组:(2)、解不等式组:
-
16、定义新运算:对于任意实数a , b都有 , 等式右边都是通常的加、减、乘法运算,比如: . 若不等式组恰有4个整数解,则实数a的取值范围是 .
-
17、某次数学竞赛中,共有20道题,评分标准是:答对一题得5分,答错或不答1题扣一分,某同学想要超过72分,他至少要答对道题.
-
18、设的整数部分为 , 小数部分为 , 则的平方根是 .
-
19、已知点在y轴上,则点P的坐标为 .
-
20、如图,对分别作下列变换:①先以x轴为对称轴作轴对称图形,然后再向左平移4个单位;②以点O为中心顺时针旋转 , 然后再向左平移2个单位;③先以y轴为对称轴作对称图形,然后再向下平移3个单位;其中能使变成的是( )
 A、① B、② C、②或③ D、①或③
A、① B、② C、②或③ D、①或③