相关试卷
-
1、现有三张不透明的卡片,它们的背面完全一样,正面分别写有数字 , 1,2,现将三张卡片背面朝上,洗匀后放在桌子上.(1)、从中随机抽取一张卡片,正面的数字是负数的概率为 .(2)、从中随机抽取一张卡片,记下数字后放回,再随机抽取一张,记下卡片上的数字,请用列表法或画树状图的方法计算这两个数的积大于0的概率.
-
2、某校为满足学生课外活动的需求,准备开设五类运动项目,分别为:篮球,:足球,:乒乓球,:羽毛球,:跳绳.为了解学生的报名情况,现随机抽取九年级部分学生进行调查,并根据调查结果绘制了如图所示的两幅不完整的统计图.
 (1)、此次调查共抽取了名学生,在扇形统计图中,项目所对应的扇形圆心角的度数为;(2)、请将条形统计图补充完整;(3)、学生小聪和小明各自从 , , 三个运动项目中任选一项参加,请利用画树状图或列表的方法求他们选择相同项目的概率.
(1)、此次调查共抽取了名学生,在扇形统计图中,项目所对应的扇形圆心角的度数为;(2)、请将条形统计图补充完整;(3)、学生小聪和小明各自从 , , 三个运动项目中任选一项参加,请利用画树状图或列表的方法求他们选择相同项目的概率. -
3、某中学九()班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球,篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了个兴趣小组,并绘制成如图所示的两幅不完整的统计图(要求每位学生只能选择一种自己喜欢的球类),

根据图中信息解答下列问题:
(1)、九()班的学生人数为 ▲ , 并把条形统计图补充完整;(2)、扇形统计图中 , , 表示“排球”的扇形的圆心角是度;(3)、排球兴趣小组名学生中有男女,现在打算从中随机选出名学生参加学校的排球队,请用列表或画树状图的方法求选出的名学生恰好是男女的概率. -
4、为了让学生了解航天航空知识,某学校组织学生参加了“航天航空知识网络答题”活动,并随机抽取了部分学生的答题成绩(满分100分)进行统计,按成绩分为五组:A . ;B . ;C . ;D . ;E . . 根据统计结果,绘制了如下两幅不完整的统计图.

根据以上信息,解答下列问题.
(1)、本次调查一共随机抽取了 ▲ 名学生的答题成绩,并补全频数直方图;(2)、求扇形统计图中E组所对应扇形的圆心角的度数;(3)、学校将从获得满分的5名同学(其中有2名男生,3名女生)中随机抽取2名同学参加演讲,请利用列表或画树状图的方法,求抽中的同学中恰有1名男生和1名女生的概率. -
5、4月15日是全民国家安全教育日.成都某校为了解全校学生对国家安全知识的了解情况,从中随机抽取了部分学生进行安全知识测试(满分100分),根据测试结果把学生分为五组:A . ;B . ;C . ;D . ;E . , 并绘制了如下不完整的频数直方图和扇形统计图.

根据以上信息,解答下列问题.
(1)、扇形统计图中 ▲ , ▲ , 并补全频数直方图;(2)、该校共有1800名学生,若成绩在70分以下的学生安全意识不强,需要进一步加强安全教育,则该校安全意识不强的学生约有多少人?(3)、若九(2)班被抽取的4名学生(3名男生和1名女生)的成绩均在E组,班主任准备在这4名学生中随机抽取2名学生作为代表发表感言,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率. -
6、对于不为零的两个实数a , b , 如果规定a★b= , 那么函数y=x★3的图象大致是( )A、
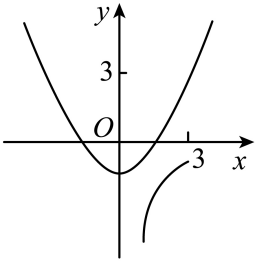 B、
B、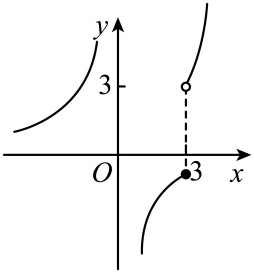 C、
C、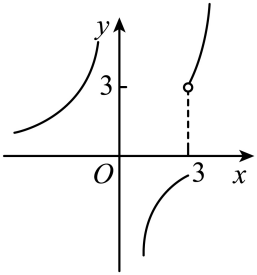 D、
D、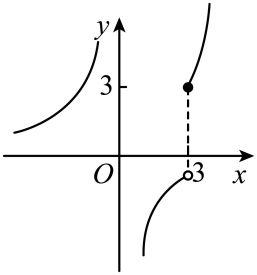
-
7、如图,菱形ABCD的对角线AC , BD相交于点O , P为AB边上一动点(不与点A , B重合),PE⊥OA于点E , PF⊥OB于点F , 若 , , 设 , 的面积是y , 则下列图像能大致反映y与x的函数关系是( )
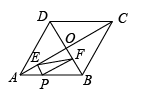 A、
A、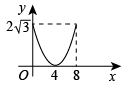 B、
B、 B.
C、
B.
C、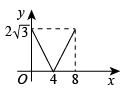 D、
D、
-
8、二次函数的图象大致为( )A、
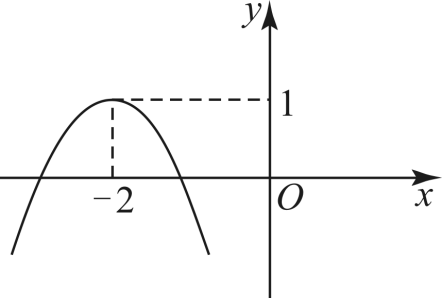 B、
B、 C、
C、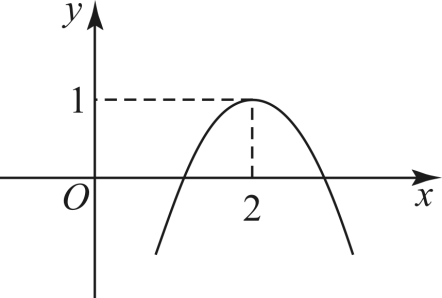 D、
D、
-
9、在同一平面直角坐标系中,二次函数与一次函数的图象大致是( )A、
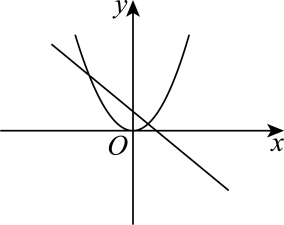 B、
B、 C、
C、 D、
D、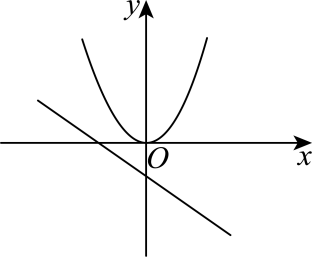
-
10、函数与在同一直角坐标系中的大致图象可能是( )A、
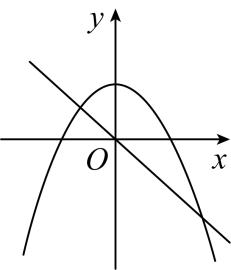 B、
B、 C、
C、 D、
D、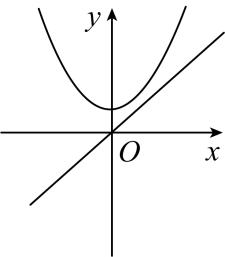
-
11、已知点 , , 都在二次函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、
-
12、抛物线经过三点,则的大小关系正确的是( )A、 B、 C、 D、
-
13、抛物线的开口方向、顶点坐标分别是( )A、开口向下,顶点坐标为 B、开口向下,顶点坐标为 C、开口向上,顶点坐标为 D、开口向上,顶点坐标为
-
14、下列对二次函数的图像描述不正确的是( )A、开口向下 B、顶点坐标为 C、与轴相交于点 D、当时,函数值随的增大而减小
-
15、关于二次函数 , 下列说法正确的是( )A、函数图象的开口向下 B、对称轴为直线 C、该函数有最大值,最大值是0 D、当时,随的增大而减小
-
16、关于x的二次函数与的性质中,下列说法错误的是( )A、开口方向相同 B、对称轴相同 C、开口大小相同 D、当时,随x的增大而减小,随x的增大而增大
-
17、在同一坐标系内, , , 的图象,它们的共同特点是( )A、都是关于原点对称,抛物线的开口方向向上 B、都是关于轴对称,随增大而增大 C、都是关于轴对称,随增大而减少 D、都是关于轴对称,抛物线顶点都是原点
-
18、抛物线的共同性质是( )A、开口向上 B、都有最大值 C、对称轴都是轴 D、顶点都是原点
-
19、已知地面温度是 , 如果从地面开始每升高 , 气温下降 , 那么气温t与高度的函数关系是( )A、正比例函数 B、反比例函数 C、二次函数 D、一次函数
-
20、下列函数是二次函数的是( )A、 B、 C、 D、