相关试卷
-
1、/span>、有两个可以自由转动的均匀转盘A , B . 转盘A被平均分成4等份,分别标上 , 2,6,8四个数字;转盘B被平均分成3等份,分别标上 , , 3三个数字.自由转动转盘A与B , 转盘停止后,指针各指向一个数字(指向分界线时重新转),把A转盘指的数字作为被除数,B转盘指针指的数字作为除数,计算这两个数的商.小贝和小晶用以上两个转盘做游戏,规则是:若这两数的商为负整数,则小贝赢;若这两个数的商为正数,则小晶赢.你认为该游戏公平吗?请你用画树状图或列表的方法,说明是否公平;如果不公平,请你修改游戏规则,使游戏公平.
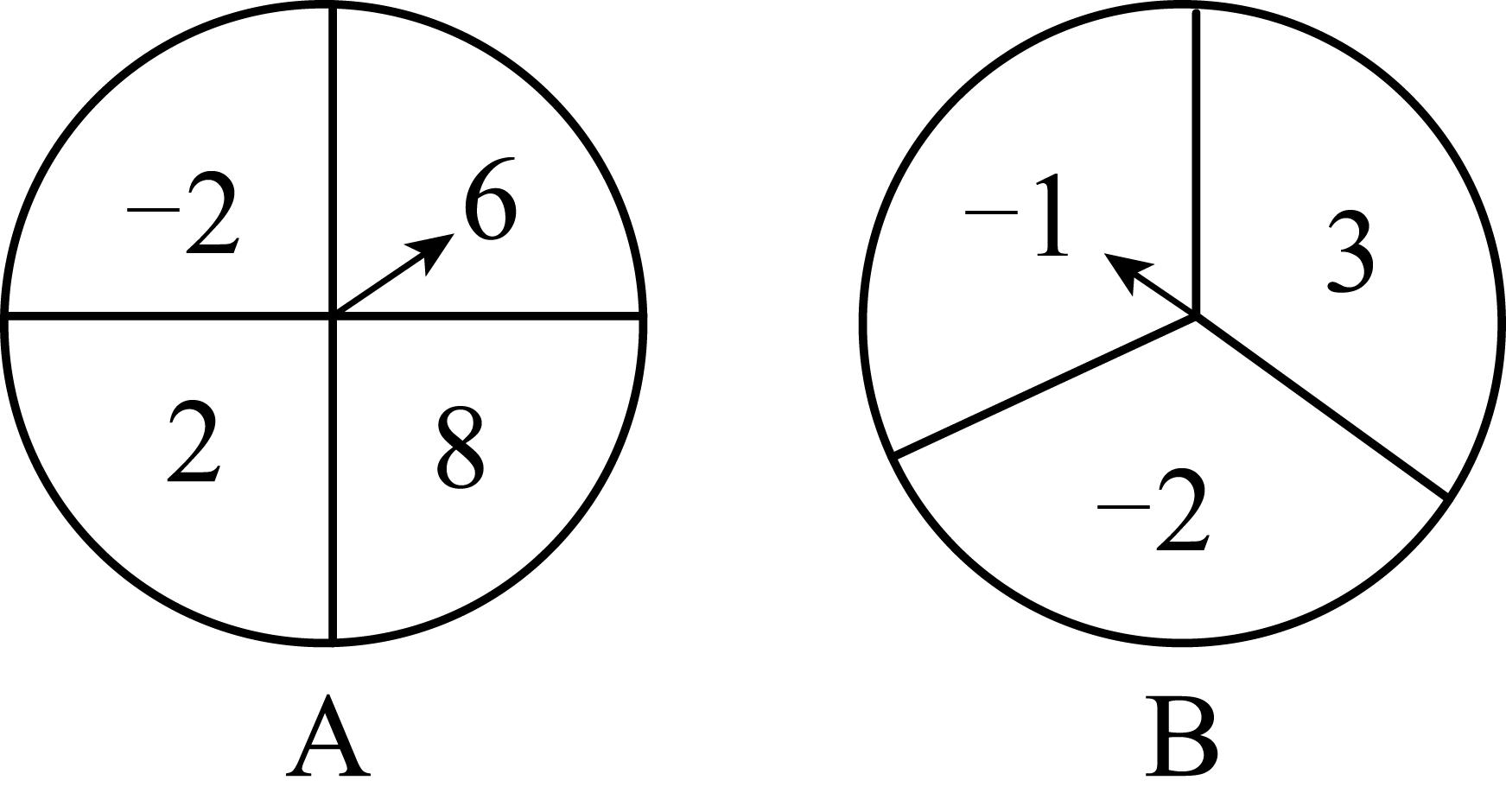
-
2、/span>、七(1)班同学设计用频率去估计概率的试验如下:在一个不透明的口袋中,装有6个球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验,统计了黄球出现的次数,绘出的统计图如图所示,则袋子中黄球的个数最可能是个.
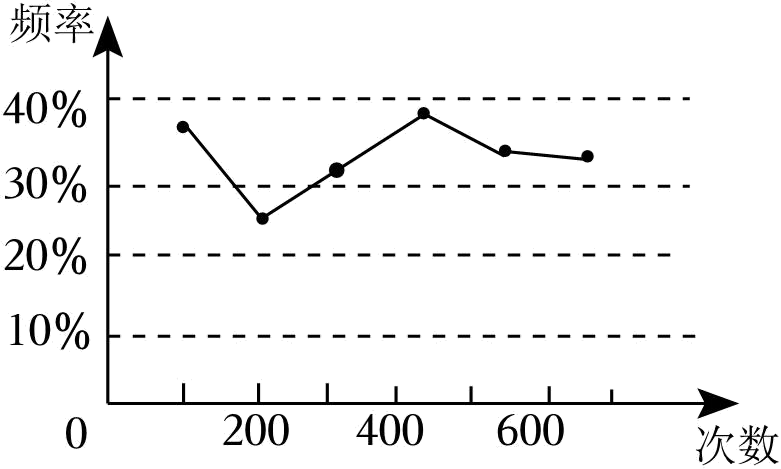
-
3、/span>、在一次大量重复试验中,统计了某一结果出现的频率.绘制出的统计图如图所示,符合这一试验结果的可能是( )
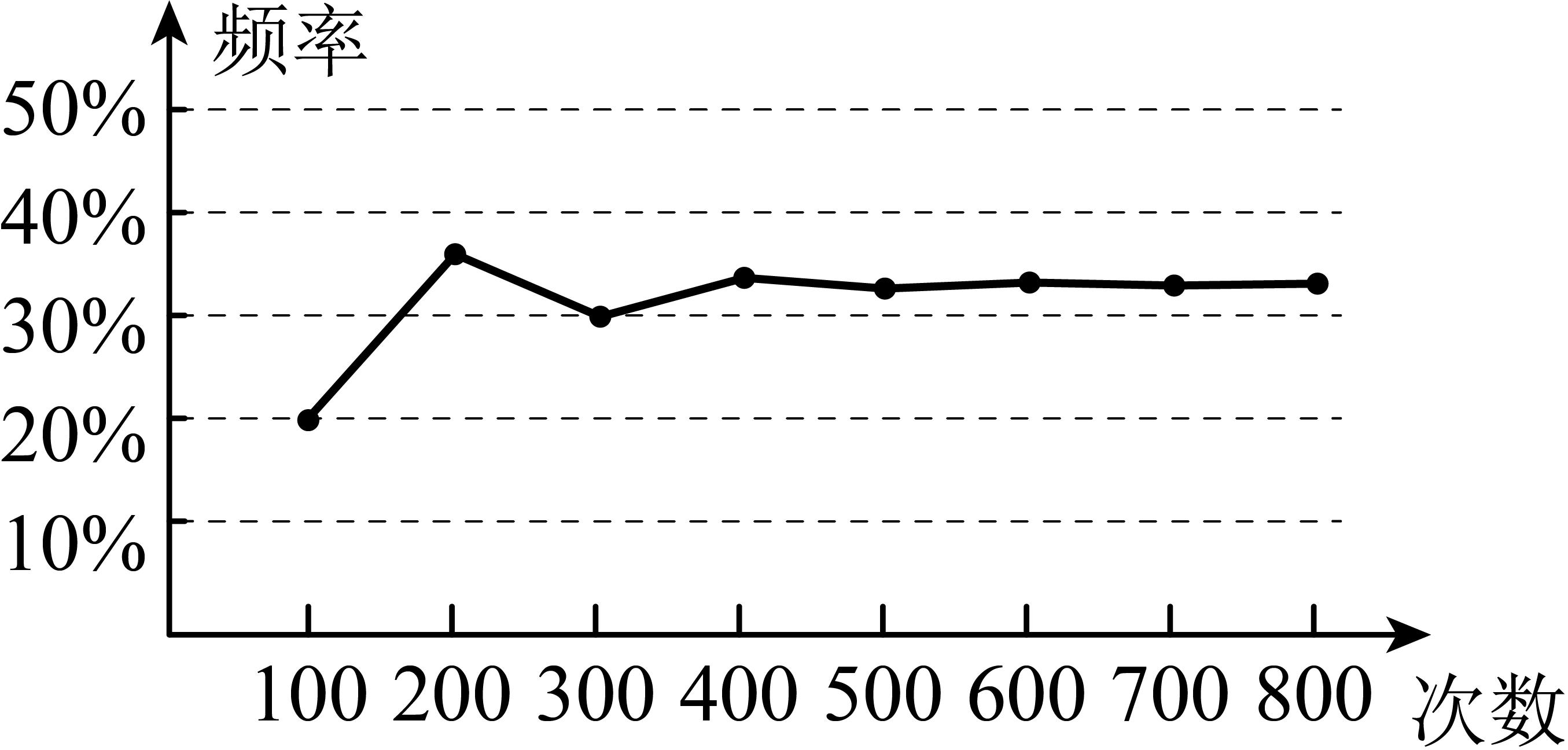 A、掷一枚质地均匀的骰子,出现2点朝上 B、从一个装有大小相同的2个蓝球和1个白球的不透明袋子中随机取一球,取到白球 C、抛一枚1元钱的硬币,出现反面朝上 D、从标有数字1到10的十张大小相同的纸牌中随机抽取一张,是奇数
A、掷一枚质地均匀的骰子,出现2点朝上 B、从一个装有大小相同的2个蓝球和1个白球的不透明袋子中随机取一球,取到白球 C、抛一枚1元钱的硬币,出现反面朝上 D、从标有数字1到10的十张大小相同的纸牌中随机抽取一张,是奇数 -
4、/span>、一只不透明的袋中装有除颜色外都相同的红球、黄球、白球共50个.通过多次摸球试验后,发现摸到红球、黄球的频率分别是 . 则可估计袋中白球的个数是( )A、10 B、15 C、25 D、20
-
5、/span>、都相同.将袋中小球摇匀,从中随机摸出一个小球记下颜色后放回,记作随机摸球一次.(1)、随机摸球10次,其中摸出黄球3次,则这10次摸球中,摸出黄球的频率是 .(2)、随机摸球2次,用画树状图或列表的方法,求这两次摸出的小球都是红球的概率.
-
6、/span>、近日,甘肃天水这座历史悠久的文化古城,因一碗麻辣烫而迅速走红网络,成为旅游新热点.自天水火爆“出圈”以来,各级团组织迅速行动起来,全面承担起志愿服务工作,同时带领一大批青年志愿者积极响应团组织号召投入志愿服务工作.根据实际需要,志愿者被陆续分配到四合院美味城网红麻辣烫店、机场、火车站等区域开展志愿服务工作.某段时间内经过抽样调查,发现志愿者服务的区域主要有A , B , C , D , E五个.抽样调查的统计结果如下表, 则下列说法不正确的是( )
区域
A
B
C
D
E
人数
A、去区域服务的人数最少 B、去区域服务的人数的频率是 C、若有名志愿者参与服务,则约有人被分配到C区域服务 D、这次抽样调查的样本容量是 -
7、/span>、调查某班 名同学的跳高成绩时,在收集到的数据中,不足 米的数出现的频率是 , 则达到或超过 米的数出现的频率是 ( )A、 B、 C、 D、
-
8、下列说法错误的是( )A、了解一批灯泡的使用寿命应采用抽样调查 B、随着试验次数的增加,频率一般会越来越接近概率 C、一组数据 , , , 的平均数是3,方差是2,则新数据 , , , 的平均数是5,方差是4 D、“367人中至少有2人的生日是同一天”是必然事件
-
9、下列说法中正确的是( )A、小明在装有红绿灯的十字路口,“遇到红灯”是随机事件 B、确定事件发生的概率是1 C、抛掷一枚质地均匀的正方体骰子600次,点数为1与点数为6的频率相同 D、从某校1000名男生中随机抽取2名进行引体向上测试,其中有一名成绩不及格,说明该校的男生引体向上成绩不及格
-
10、下列说法正确的是( )A、“汽车累计行驶 , 从未出现故障”是不可能事件 B、“买中奖率为的奖券张,中奖”是必然事件 C、投掷一枚图钉,“钉尖朝上”的概率可以用列举法求得 D、通过大量重复试验,可以用频率估计概率
-
11、礼泉历史悠久,自秦始皇二十六年(前221年)建县,已有2200多年历史.境内有古文化遗址21处,古建筑5处,是陕西省18个重点文物旅游大县之一.某数学小组制作了四张礼泉县的风景名胜卡片,卡片除正面内容不同之外,其他完全相同,卡片正面内容如图所示:
 (1)、将四张卡片背面朝上,洗匀后,从第随机抽取一张,恰好抽到“C . 礼泉文庙”的概率是;(2)、将四张卡片骩于暗箱摇匀,随机抽取一张不放回,然后再随机抽取一张,请利用画树状图或列表的方法求抽取的两张卡片恰好是“A . 昭陵”和“D . 顶天寺”的概率.(不考虑所抽取卡片的顺序)
(1)、将四张卡片背面朝上,洗匀后,从第随机抽取一张,恰好抽到“C . 礼泉文庙”的概率是;(2)、将四张卡片骩于暗箱摇匀,随机抽取一张不放回,然后再随机抽取一张,请利用画树状图或列表的方法求抽取的两张卡片恰好是“A . 昭陵”和“D . 顶天寺”的概率.(不考虑所抽取卡片的顺序) -
12、寒假期间,小赵的爸爸准备带小赵去广安旅游.由于时间关系,原计划去的华蓥山和天意谷只能去其中一个,现决定用抽扑克牌的方式来决定,具体方法如下:把四张牌面数字分别是2,3,4,5的扑克牌背面向上放置于桌面上,洗匀后,小赵先从中任意抽出一张,然后爸爸再从剩下的三张中任意抽出一张,如果两人的牌面数字之和大于7,就去华蓥山;否则,就去天意谷.(1)、如果小赵抽出的牌面数字是4,那么他们去华蓥山的概率为;(2)、请利用画树状图或列表的方法分析他们去华蓥山和天意谷哪个地方的概率大.
-
13、甲骨文是迄今为止中国发现的年代最早的成熟文字系统,是汉字的源头和中华优秀传统文化的根脉,赵星在了解甲骨文后,制作了如图所示的四张卡片(这四张卡片分别用字母A , B , C , D表示,正面文字依次是文、明、自、由,这四张卡片除正面内容不同外,其余均相同),现将四张卡片背面朝上,洗匀放好.
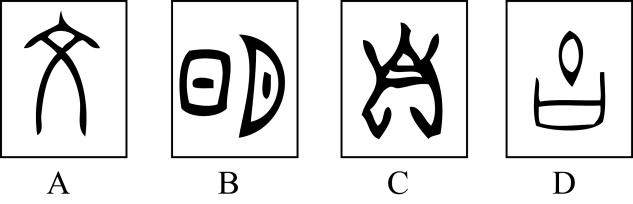 (1)、赵星从中随机抽取一张卡片,所抽取的卡片上的文字是“文”的概率为 .(2)、赵星从中随机抽取一张卡片不放回,张涵再从中随机抽取一张卡片,请用列表或画树状图的方法计算两人抽取的卡片恰好组成“自由”一词的概率.
(1)、赵星从中随机抽取一张卡片,所抽取的卡片上的文字是“文”的概率为 .(2)、赵星从中随机抽取一张卡片不放回,张涵再从中随机抽取一张卡片,请用列表或画树状图的方法计算两人抽取的卡片恰好组成“自由”一词的概率. -
14、已知一只不透明的箱子中装有除颜色外完全相同的红、黄、蓝色球共30个,从中任意摸出一个球,摸到红、蓝球的概率分别为0.2和0.5.(1)、试求黄色球的数量;(2)、若向箱中再放进a个红球,这时从纸箱中任意摸出一球是红球的概率为 , 求a的值.
-
15、在一个不透明的袋子中装有6个红球和9个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.(1)、求出摸出的球是黄球的概率;(2)、为了使摸出两种球的概率相同,再放进去9个同样的红球或黄球,那么这9个球中,红球和黄球的数量分别应是多少?
-
16、一个不透明的袋中装有3个黄球,17个黑球和20个红球,它们除颜色外都相同.(1)、求从袋中摸出一个球是黄球的概率;(2)、现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率是 , 则取出了个黑球.(直接填空)
-
17、一个正方体骰子,其中一个面上标有“1”,两个面上标有“2”,三个面上标有“3”,求这个骰子掷出后:(1)、“2”朝上的概率;(2)、朝上概率最大的数;(3)、如果规定出现朝上的数为1或2时甲胜,出现朝上的数为3时,乙胜,那么甲、乙谁获胜的机会大些.
-
18、现有两个盒子,甲盒装有红球5个,白球2个和黑球3个,乙盒装有红球20个,白球20个和黑球10个.(1)、如果随机取出1个黑球,从盒中抽取成功的机会大;(2)、小明同学说:“从乙盒中取出10个红球后,乙盒中的红球个数比甲盒中红球个数多,所以此时想取出1个红球,选乙盒成功的机会大.”请利用概率的知识判断小明的说法是否正确.
-
19、在3张相同的小纸条上分别写有“石头”、“剪子”、“布”.将这3张小纸条做成3支签,放在不透明的盒子中搅匀.(1)、从盒子中任意抽出1支签,抽到“石头”的概率是;(2)、甲、乙两人通过抽签分胜负,规定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”.甲先从盒子中任意抽出1支签(不放回),乙再从余下的2支签中任意抽出1支签,求甲取胜的概率.
-
20、一个不透明的口袋里装有5个红球,3个白球,2个绿球,这些球形状和大小完全相同,小明从中任意摸出一个球.(1)、你认为小明摸到的球很可能是什么颜色?为什么?(2)、摸到三种颜色球的可能性一样吗?(3)、如果想让小明摸到红色球和白色球的可能性一样,该怎么办?写出你的方案.