相关试卷
-
1、如图,是的边上的中线,是的边上的中线,是的边上的中线,连接 , . 若的面积是 , 则阴影部分的面积是 .

-
2、等腰三角形的一个角等于 , 则它的顶角的度数是 .
-
3、如图,根据用直尺、圆规作一个角等于已知角的方法,画出了 . 则的理由是 .
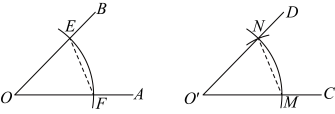
-
4、一个三角形的三边分别是x , 3,5,那么这个三角形的边长的取值范围是 .
-
5、如图,可以看作是沿直线平移得到的.如果 , 那么线段的长是 .

-
6、如图,一个粒子在第一象限内及轴、轴上运动,在第一分钟,它从原点运动到点 , 第二分钟,它从点运动到点 , 而后它接着按图中箭头所示在与轴,轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2024分钟时,这个粒子所在位置的坐标是( )
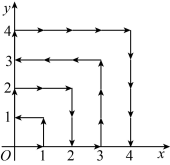 A、 B、 C、 D、
A、 B、 C、 D、 -
7、能判定的条件是( )A、 B、 C、 D、
-
8、已知是方程的解,则( )A、1 B、 C、3 D、
-
9、以下问题,适合全面调查的是( )A、了解一批灯泡的使用寿命 B、疫情期间,对进入学校的全体师生进行体温检测 C、了解全市学生网课期间每周体育锻炼时间 D、调查春节晚会的收视率
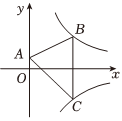
-
10、如图1,将正方形纸片ABCD沿过点B的直线折叠,使点A落在正方形ABCD内部,点A的对应点为点G , 折痕为BE , 再将该纸片沿过点B的直线折叠,使BC与BG重合,折痕为BF.
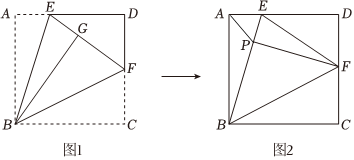 (1)、求∠EBF的度数.(2)、将图1折叠所得的图形重新展开并铺平.如图2,连结EF , 作FP垂直BE于点P , 连结AP.
(1)、求∠EBF的度数.(2)、将图1折叠所得的图形重新展开并铺平.如图2,连结EF , 作FP垂直BE于点P , 连结AP.①求证:;
②记 , , 求y关于x的函数表达式.
-
11、综合与实践:如何称量一个空矿泉水瓶的重量?
素材1:如图是一架自制天平,支点O固定不变,左侧托盘固定在点A处,右侧托盘的点P可以在横梁BC段滑动.已知OA=OC=12cm , BC=28cm , 一个100g的砝码.
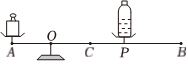
素材2:由于一个空的矿泉水瓶太轻无法称量,小组进行如下操作:左侧托盘放置砝码,右侧托盘滑动点P至点B , 空瓶中加入适量的水使天平平衡,再向瓶中加入等量的水,发现点P移动到PC长12cm时,天平平衡.
链接:根据杠杆原理,平衡时:左盘砝码重量×OA=右盘物体重量×OP.(不计托盘与横梁重量)
(1)、任务1:设右侧托盘放置y(g)物体,OP长x(cm),求y关于x的函数表达式,并求出y的取值范围.(2)、任务2:求这个空矿泉水瓶的重量. -
12、如图,在四边形ABCD中,AD∥BC , AB=BC , 对角线AC , BD交于点O , BD平分∠ABC.
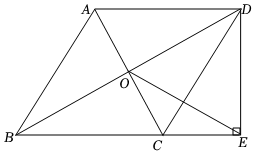 (1)、求证:四边形ABCD是菱形.(2)、过点D作DE⊥BC , 交BC的延长线于点E , 连接OE , 若AC=8,CD=6,求OE的长.
(1)、求证:四边形ABCD是菱形.(2)、过点D作DE⊥BC , 交BC的延长线于点E , 连接OE , 若AC=8,CD=6,求OE的长. -
13、已知关于x的一次函数y=2ax+x-a+1(a为常数,且a≠0).(1)、当自变量1对应的函数值为5时,求a的值;(2)、对任意非零实数a , 一次函数的图象都经过点Q , 请求点Q的坐标.
-
14、随着互联网络快速发展,人工智能软件已渗透进我们的生活,某平台抽取用户对甲、乙两款人工智能软件进行评分,将收集到的评分数据进行整理、描述和分析.下面给出了部分信息.对甲款人工智能软件抽取的20条评分数据为:64,70,75,76,78,78,85,85,85,85,86,89,90,90,94,95,98,98,99,100.对乙款人工智能软件共抽取20条评分数据,记为xi(i=1,2,3…,20),将数据先从小到大整理为A , B , C , D四组绘制成如下扇形统计图,C组包含的所有数据为:
85,86,87,88,88,88,90,99.(A:60<xi≤70,B:70<xi≤80,C:80<xi≤90,D:90<xi≤100)

甲、乙两款人工智能软件的评分统计表
软件
平均数
中位数
众数
甲
86
85.5
a
乙
86
b
88
根据以上信息,解答下列问题:
(1)、填空:a= , m= , b=.(2)、若本次调查有600名用户对甲款人工智能软件进行了评分,估计其中对甲款人工智能软件非常满意(90<x≤100)的用户人数. -
15、如图,四边形ABCD的对角线AC , BD相交于点E , AC=AD , ∠ACB=∠ADB , 点F在ED上,∠BAF=∠EAD.
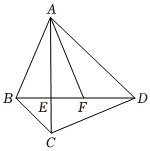 (1)、求证:△ABC≌△AFD;(2)、若BE=FE , ∠ABD=70°,求∠EAF的度数.
(1)、求证:△ABC≌△AFD;(2)、若BE=FE , ∠ABD=70°,求∠EAF的度数. -
16、解不等式组: , 并把解集表示在数轴上.
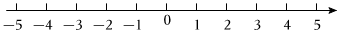
-
17、(1)、计算:.(2)、解方程组:.
-
18、如图,在ABCD为矩形中,AC为对角线,将△ABC沿AC翻折,点B的对应点为点B'.AB'与CD相交于点E , 延长CB'与AD相交于点F , 已知AB=4,BC=3,则EC的长为;△ACF的面积为.
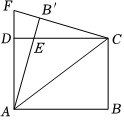
-
19、如图,在平行四边形ABCD中,点E是AB上一点, , 连接DE并延长交CB的延长线于点F.连接CE , 过点A作AG∥EC交DE于点G , 若AG=10,则CE的长为.
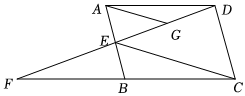
-
20、如图,点A是y轴上一点,点B , C分别在反比例函数y=(a>0,x>0)和y=(b<0,x>0)的图象上,且BC∥y轴,若△ABC的面积为6,则a-b的值为.