-
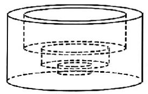
1、如图,在一个半径为4厘米,高为4厘米的圆柱的中间依次向下挖去半径分别为3厘米、2厘米、1厘米,高分别为2厘米、1厘米、0.5厘米的圆柱,则最后得到的立体图形的表面积是平方厘米(结果保留π).
-
2、如图所示的图案是用一把直尺、含60°角的三角尺和光盘摆放而成的,A为直角三角尺的斜边与直尺的交点,B为光盘与直尺的唯一交点.若AB=3,则光盘的直径是.

-
3、 如图,在菱形ABCD 中, 则tan∠DBE 的值为.

-
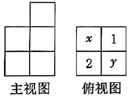
4、由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小正方体的个数,则x+y=.
-
5、 如图,⊙O 内切于Rt△ABC,点 P,Q分别在直角边BC、斜边AB 上,PQ____AB,且PQ与⊙O 相切.若AC=2PQ,则 tanB 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
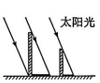
6、如图,太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上投影的长是 , 则皮球的直径是( )
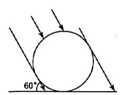 A、 B、15cm C、10cm D、
A、 B、15cm C、10cm D、 -
7、一艘货轮从小岛A 正南方向的点B 处向西航行30km到达点C 处,然后沿北偏西60°方向航行20km到达点 D 处,此时观测到小岛A 在北偏东60°方向,则小岛A 与出发点B 之间的距离为( )
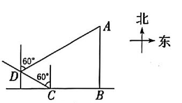 A、 B、 C、 D、
A、 B、 C、 D、 -
8、 如图,在四边形ABCD 中, , O为AB 的中点,以点O为圆心,AO长为半径作圆,恰好使得点 D 在⊙O 上,连结OD,若 则下列说法中,错误的是( )
 A、D 是 的中点 B、CD 是⊙O 的切线 C、AE∥OD D、
A、D 是 的中点 B、CD 是⊙O 的切线 C、AE∥OD D、 -
9、如图,以正六边形ABCDEF 的顶点A 为圆心,AB 长为半径作⊙A,与正六边形ABCDEF 重合的扇形部分恰好是一个圆锥的侧面展开图,则该圆锥的底面半径与母线长之比为( )
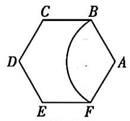 A、 B、 C、 D、12
A、 B、 C、 D、12 -
10、 如图,AB 是⊙O的直径,C,D 是⊙O上的点,∠CDB=15°,过点C作⊙O 的切线交AB 的延长线于点E,则 sin E 的值为( )
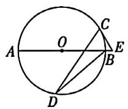 A、12 B、 C、 D、
A、12 B、 C、 D、 -
11、 如图, M是边OA 上一点,以点M 为圆心,3cm为半径作⊙M.当OM=5cm时,⊙M 与直线OB 的位置关系是( )
 A、相离 B、相交 C、相切 D、无法确定
A、相离 B、相交 C、相切 D、无法确定 -
12、 在△ABC 中,若 则△ABC为( )A、直角三角形 B、等边三角形 C、含 60°角的任意三角形 D、顶角是钝角的等腰三角形
-
13、下列物体的影子中,不正确的是( )A、
 B、
B、 C、
C、 D、
D、
-
14、篆刻是中华传统艺术之一,雕刻印章是篆刻基本功.如图所示为一块雕刻印章的材料,其俯视图为( )
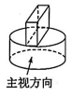 A、
A、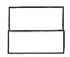 B、
B、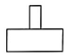 C、
C、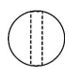 D、
D、
-
15、综合与实践课上,老师让同学们以“三角形的角与三角形的特殊线段”为主题开展数学活动.

 (1)、【操作判断】在△ABC中,∠B=40°,∠C=70°,作∠BAC 的平分线AD交BC于点 D.
(1)、【操作判断】在△ABC中,∠B=40°,∠C=70°,作∠BAC 的平分线AD交BC于点 D.①操作一:在图(1)中,用三角尺作 BC 边上的高AE,垂足为点 E,求∠DAE的度数;
②操作二:如图(2),在 AD 上任取点 F,作FE⊥BC,垂足为点 E,直接写出∠DFE 的度数.
(2)、【迁移探究】如图(3),将操作二中“在AD上任取点 F”改为“在DA 的延长线上任取点F”,其他条件不变,判断∠DFE 的度数是否会发生变化,并说明理由.(3)、【拓展应用】如图(4)、图(5),在△ABC中,∠ABC=α,∠ACB=β,AD 是∠BAC 的平分线,在直线AD 上任取点 F,过点 F 作EF⊥AD与直线 BC 交于点 E,请求出∠DEF 与α,β之间的数量关系. -
16、如图,△ABC中,AD是 BC 边上的高,AE 是∠BAC 的平分线,∠EAD=15°,∠B=50°,求∠C的度数.

-
17、
 (1)、探究:如图(1),在△ABC 中,∠ACB=90°,CD⊥AB 于点 D,若∠B=30°,则∠ACD 的度数是°;(2)、拓展:如图(2),∠MCN=90°,射线 CP 在∠MCN 的内部,点A,B分别在 CM,CN上,分别过点A,B 作AD⊥CP,BE⊥CP,垂足分别为D,E,若∠CBE=70°,求∠CAD 的度数;(3)、应用:如图(3),点A,B 分别在∠MCN 的边CM,CN上,射线CP 在∠MCN 的内部,点D,E在射线 CP 上,连结AD,BE,若∠ADP=∠BEP = 60°, 则 ∠CAD+∠CBE +∠ACB =°.
(1)、探究:如图(1),在△ABC 中,∠ACB=90°,CD⊥AB 于点 D,若∠B=30°,则∠ACD 的度数是°;(2)、拓展:如图(2),∠MCN=90°,射线 CP 在∠MCN 的内部,点A,B分别在 CM,CN上,分别过点A,B 作AD⊥CP,BE⊥CP,垂足分别为D,E,若∠CBE=70°,求∠CAD 的度数;(3)、应用:如图(3),点A,B 分别在∠MCN 的边CM,CN上,射线CP 在∠MCN 的内部,点D,E在射线 CP 上,连结AD,BE,若∠ADP=∠BEP = 60°, 则 ∠CAD+∠CBE +∠ACB =°. -
18、问题情境:

如图(1)所示的图形像我们常见的学习用品——圆规.我们不妨把这样的图形叫作“规形图”.
(1)、探究发现:观察“规形图”,试探究∠D 与∠BAC,∠B,∠C 之间的数量关系,并说明理由;
(2)、解决问题:请你利用以上结论,解决下列问题:
①如图(2),把一块含45°角的三角尺DEF 放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点 B,C, 若 ∠A = 40°, 则 ∠ABD +∠ACD=°;
②如图(3),BD平分∠ABP,CD平分∠ACP,若∠A=40°,∠P=130°,则∠D 的度数为.
-
19、如图,∠ABD,∠ACD的平分线交于点 P,若∠A=55°,∠D=15°,则∠P 的度数为( )
 A、15° B、20° C、25° D、30°
A、15° B、20° C、25° D、30° -
20、如图,将三角形纸片ABC 沿 DE 折叠,当点 A 落在四边形 BCED的外部点A'处时,测得∠1=70°,∠2=140°,则∠A 的度数为( )
 A、25° B、30° C、35° D、40°
A、25° B、30° C、35° D、40°