-
1、(1)、请你把下列各数填入表示它所在的数集的圈里:
, , , .
 (2)、这四种数的集合合并在一起(选填“是”或“不是”)全体有理数集合.
(2)、这四种数的集合合并在一起(选填“是”或“不是”)全体有理数集合. -
2、定义一种新运算:对于任意有理数 , , 满足当 , 时,的最大值为.
-
3、下图是一数值转换机,输入数值后按两个方框中的程序运算,若运算结果大于100,可以输出结果;若运算结果不大于100,则将得到的结果重新输入,进行运算,直到运算结果大于100时输出运算结果.当输入的数为20时,最终输出的结果是.

-
4、嘉淇在写作业的时候,不慎将一滴墨水滴在数轴上,根据如图所示的数据,则墨迹遮盖的整数中满足绝对值大于1.5并且小于或等于3的整数有个.

-
5、的倒数是;的相反数是.
-
6、如图,将 , , , 分别填入没有数字的圈内,使横、竖以及内、外两圈上的4个数之和都相等,则 , 所在位置的两个数之和是( )
 A、或2 B、或2 C、或1 D、或
A、或2 B、或2 C、或1 D、或 -
7、如图,在数轴上点 , , 表示有理数 , , , 若 , , 则下面四个结论:;;; , 其中一定成立的结论有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
8、若 , 为有理数,且 , 则的值为( )A、0 B、1 C、 D、
-
9、纽约与北京的时差为(同一时刻北京时间为7:00,东京时间为8:00,那么东京与北京的时差为1h).小明在北京乘坐早晨10:00的航班飞行约到达纽约,那么小明到达时纽约时间是( )A、15时 B、16时 C、17时 D、18时
-
10、当温度每上升时,某种金属丝伸长.反之,当温度每下降时,该金属丝缩短.把的金属丝冷却到 , 再加热到 , 最后的长度比原来伸长了( )A、 B、 C、 D、
-
11、要使算式的计算结果最大,在“”里填入的运算符号应是( )A、 B、- C、× D、
-
12、已知 , , 且 , 则的值为( )A、3或7 B、或 C、 D、
-
13、若 , 互为相反数, , 互为倒数,的绝对值是 , 则的值为( )A、1 B、 C、1或 D、1或
-
14、下列计算正确的是( )A、 B、 C、 D、
-
15、把写成省略加号及括号的形式是( )A、 B、 C、 D、
-
16、如图①,点 , , 依次在直线上,将射线绕点沿顺时针方向以每秒 的速度转动,同时将射线绕点沿逆时针方向以每秒 的速度转动(如图②),设转动时间为秒.
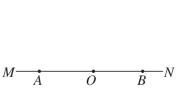

① ②
(1)、 , .(均用含 的代数式表示)(2)、在转动过程中,当时,求的值.(3)、在转动过程中,是否存在这样的 , 使得射线是由 , , 中的两条射线组成的角(指大于而不超过的角)的平分线?若存在,请求出的值;若不存在,请说明理由. -
17、定义:关于的方程与( , 均为不等于0的常数)称互为“反对方程”.例如:方程与互为“反对方程”;方程 , 通过转化可得 , 所以与互为“反对方程”.(1)、若关于的方程与(为不等于0的常数)互为“反对方程”,则;(2)、若关于的方程(为不等于0的常数)的解为 , 求的值及它的“反对方程”的解;(3)、若关于的方程(为不等于0的常数)的解为 , 请直接写出的解.
-
18、环形跑道一圈长 , 小明同学在跑道上练习骑自行车,平均每分钟骑;小军同学在跑道上练习跑步,起初平均每分钟跑.(1)、若两人从同一处同时反向出发,经过多长时间两人首次相遇?(2)、若两人从同一处同时同向出发,小军同学跑1分钟后,体能下降,平均速度下降到每分钟跑 , 经过多长时间两人首次相遇?
-
19、有一个数学游戏,如图,一个数从 , , 三个位置中任选一个位置出发,按照通道内标注的要求进行运算到下一个位置.例如:将3按照(或)的顺序进行运算,即3经过“乘以”的运算得出结果.
 (1)、将按照的顺序进行运算,列出算式并求出运算结果.(2)、将一个数按照的顺序进行运算,发现运算结果为1.求这个数.
(1)、将按照的顺序进行运算,列出算式并求出运算结果.(2)、将一个数按照的顺序进行运算,发现运算结果为1.求这个数. -
20、在解方程时,小刚在去分母的过程中,右边的“”漏乘了公分母6,因而求得方程的解为 , 请求出的值和方程正确的解.