-
1、如果 , 则 , , 的大小关系为 .
-
2、已知a , b互为相反数,c , d互为倒数,x的绝对值为1,则= .
-
3、阅读理解:将一个数不等于0和1)作“它的相反数与1的和的倒数”的变换,逐一变换可得一组新数.例如:第1次变换得到 , 记为;第2次变换得到 , 记为;第次变换得到 , 记为 . 延伸拓展:将一个数组均不等于0和1)中的各数分别作“它的相反数与1的和的倒数”的变换,第1次变换得到 , ;第2次变换得到;第次变换得到 . 活学活用:若数组确定为 , 则的值为( )A、37 B、 C、39 D、
-
4、如图所示,在这个数据运算程序中,若开始输入的x的值为2,结果输出的是1,返回进行第二次运算则输出的是 , …,则第2024次输出的结果是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、有理数在数轴上对应的点如图所示,则 , , 1的大小关系表示正确的是( )
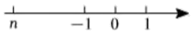 A、 B、 C、 D、
A、 B、 C、 D、 -
6、如图,数轴上点 , 对应的有理数分别为 , , 下列说法正确的是( )
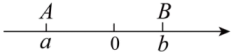 A、 B、 C、 D、
A、 B、 C、 D、 -
7、按照如图所示的操作步骤,若输入x的值为 , 则输出的值为( )
 A、59 B、-1 C、1 D、0
A、59 B、-1 C、1 D、0 -
8、数轴上的点A到的距离是5,则点A表示的数为( )A、3或 B、5或 C、 D、5
-
9、下列说法正确的是( )A、整数、分数、小数统称为有理数 B、两个有理数的和一定大于每一个加数 C、1的倒数是1 D、0是最小的有理数
-
10、星海学校占地面积78615平方米,总建筑面积104101平方米,其中数104101用科学记数法表示为( )A、 B、 C、 D、
-
11、若把气温为零上10℃记作+10℃,则-1℃表示气温为( )A、零上1℃ B、零下1℃ C、零上9℃ D、零下11℃
-
12、在7,0, , , , 中,负数有( )个A、2 B、3 C、4 D、5
-
13、如果是关于x的一元一次方程,那么方程的解为 .
-
14、圣诞节期间,某品牌圣诞树按成本价提高后标价,再打折销售,利润为元.设该圣诞树的成本价为元,根据题意,列出的方程是 .
-
15、 , 那么
-
16、中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”大意如下:有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,之后每天走的路程都为前一天的一半,一共走了六天才到关口,则此人第二天和第六天共走了里.
-
17、若方程是关于x的一元一次方程,则a= .
-
18、一批货物用载重为1.5吨的汽车比用载重为4吨的大卡车要多运5次才能运完,若设这批货物共有x吨,则可列出方程为( )A、1.5x-4x=5 B、 C、 D、
-
19、根据等式的性质,下列变形正确的是( )A、如果2x=3,那么x= B、如果x=y,那么x﹣5=5﹣y C、如果x=y,那么﹣2x=﹣2y D、如果x=6,那么x=3
-
20、若 , 则下列等式不一定成立的是( )A、 B、 C、 D、;