-
1、化简求值: , 其中 , .
-
2、化简:(1)、 ;(2)、 .
-
3、已知整式.(1)、若的值与的取值无关,则;(2)、当 , 时.
①化简;
②当整式取得最小值时,此时的值为.
-
4、一组按规律排列的单项式: , , , , , , 则第7个单项式 , 第个单项式为.
-
5、如图,长为 , 宽为的大长方形被分割为7小块,除阴影 , 外,其余5块是形状、大小完全相同的小长方形,其较短的边长为4,下列说法中错误的有( )

①每个小长方形的较长边为;
②阴影的较短边和阴影的较短边之和为;
③若为定值,则阴影和阴影的周长之和为定值;
④当时,阴影和阴影的面积之和为定值.
A、1个 B、2个 C、3个 D、4个 -
6、一个有趣的游戏:首先发给 , , 三位同学相同数量的扑克牌(假定发到每位同学手中的扑克牌数量为 , 且数量足够多),然后依次完成以下三个步骤:第一步,同学拿出三张扑克牌给同学;第二步,同学拿出五张扑克牌给同学;第三步,同学手中此时有多少张扑克牌,同学就拿出多少张扑克牌给同学.请你确定,最终同学手中剩余的扑克牌的张数为( )A、8 B、11 C、 D、
-
7、已知 , , 在数轴上的位置如图所示,则代数式的值等于( )
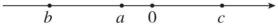 A、 B、 C、 D、0
A、 B、 C、 D、0 -
8、已知 , 那么代数式的值为( )A、8 B、10 C、12 D、16
-
9、若和都是六次多项式,则一定是( )A、12次整式 B、次数不高于6的整式 C、次数不低于6的整式 D、以上都不对
-
10、下列化简中,正确的是( )A、 B、 C、 D、
-
11、若是关于 , 的五次三项式,则的值为( )A、 B、4 C、或4 D、不存在
-
12、下列说法中,错误的是( )A、是单项式 B、的次数为1 C、的次数为1 D、的系数为
-
13、下列式子: , , , , , , 其中是多项式的有( )A、2个 B、3个 C、4个 D、5个
-
14、如图, , 为一把不完整刻度尺有刻度一侧的两端,现将其紧贴数轴摆放,已知刻度尺上“2.5”“1”两个刻度分别对应着数轴上表示数 , 的两点,且 , 两数满足.
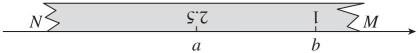 (1)、 , ;(2)、若将图①中的数轴沿水平方向移动1个单位长度,此时刻度“1.7”对应数轴上的数是多少;(3)、若刻度尺右端的刻度为“0.5”,将刻度尺沿数轴向右移动6个单位长度,此时,刻度尺的左端点恰好与数轴上表示数1的点重合,请确定这把刻度尺有刻度一侧的长度,并说明理由.
(1)、 , ;(2)、若将图①中的数轴沿水平方向移动1个单位长度,此时刻度“1.7”对应数轴上的数是多少;(3)、若刻度尺右端的刻度为“0.5”,将刻度尺沿数轴向右移动6个单位长度,此时,刻度尺的左端点恰好与数轴上表示数1的点重合,请确定这把刻度尺有刻度一侧的长度,并说明理由. -
15、进位制是人们为了记数和运算方便而约定的记数系统.约定逢十进一就是十进制,逢二进一就是二进制,也就是说“逢几进一”就是几进制,几进制的基数就是几,以此类推,进制就是逢进一.为与十进制进行区分,我们常把用进制表示的数写成进制的数转化为十进制的数的方法是:若进制表示的数为 , 则转换为十进制数的过程为规定当时,.
根据你所学的知识,完成以下问题:
(1)、把下列进制表示的数转化为十进制表示的数:① ;
② .
(2)、已知二进制数 , 请计算并写出的值(要求写成二进制表示的数).(3)、请把转换成十二进制的数. -
16、在一次抗洪救灾中,解放军驾驶冲锋舟在一条东西方向的河流中抢救灾民,早晨从地出发,晚上到达地,规定向东为正,当天航行路程单位:如下: , , , , , , , .(1)、地在地的什么位置,距地有多远?(2)、若冲锋舟每千米耗油0.45升,开始出发时,油箱中有油30升,问中途是否需要加油?若需要加油,至少需加多少升?
-
17、在数学课上,同学们遇到了这样一道题目“计算:.”嘉嘉和淇淇的解法如下:
嘉嘉:原式;
淇淇:原式.
(1)、淇淇的解法运用了哪种运算律?(2)、请你再写出一种解法. -
18、老师设计了一个接力游戏,用合作的方式完成有理数运算,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:
 (1)、在接力过程中,计算错误的学生有;(2)、请给出正确的计算过程.
(1)、在接力过程中,计算错误的学生有;(2)、请给出正确的计算过程. -
19、将下列各数: , , , 在数轴上表示出来,并用“”把它们连接起来.

-
20、计算:(1)、 ;(2)、 .