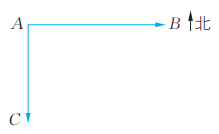
-
1、如图，甲船以15千米/时的速度从港口A向正南方向航行，乙船以20千米/时的速度同时从港口A向正东方向航行。行驶2小时后，两船相距多远?
-
2、 如图，在△ABC中，AB=AC，AB=17，BC=16。
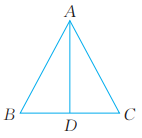(1)、求BC边上的中线AD的长。(2)、 求△ABC的面积。 -
3、利用圆规和图中数轴上方的正方形网格线，在数轴上表示 的点。
-
4、 在△ABC中，∠C=90°，BC=a，AC=b，AB=c。(1)、 若a=9，b=12，求c；(2)、 若a=9，c=41，求b；(3)、 若c=10，b=7，求a。
-
5、利用圆规和图中数轴上方的正方形网格线，在数轴上表示， 的点。
-
6、 在△ABC中，∠C=90°，AB=c，BC=a，AC=b。(1)、 若 求c；(2)、 若a=12，c=13，求b；(3)、 若c=34，a：b=8：15，求a，b。
-
7、图是一个长方形零件图。根据所给的尺寸(单位：mm)，求两孔中心A，B之间的距离。
-
8、已知在△ABC中，∠C=90°，BC=a，AC=b，AB=c。(1)、 若a=1，b=2，求c；(2)、 若a=15，c=17，求b。
-
9、如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙底端C的距离为0.7米。如果梯子的顶端沿墙面下滑0.4米，那么点B将向外移动多少米?
-
10、如图所示的钢架中，∠A=20°，焊上等长的钢条 ..来加固钢架。若 这样的钢条至多需要多少根?
-
11、已知∠O及其边上两点A和B(如图)。用直尺和圆规作一点P，使点P到∠O两边的距离相等，且到点A，B的距离也相等。
-
12、 如图，CD=BE，DG⊥BC，EF⊥BC，垂足分别为点G，F，且DG=EF。判断下列结论是否正确，并给出证明。
(1)、 BG=CF；(2)、 BD=CE。 -
13、 已知△ABC的三边a=m-n(m>n>0)，b=(1)、 求证：△ABC是直角三角形。(2)、利用第(1)题的结论，写出两个直角三角形的边长，要求它们的边长均为正整数。
-
14、 已知：如图，在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG⊥CE于G，CD=AE。求证：CG=EG。
-
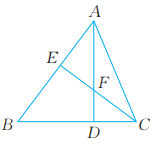
15、 已知：如图，AD是△ABC的高线，E是AB上一点，CE交AD于点F，∠AFE=∠B。求证：CE⊥AB。
-
16、 在Rt△ABC中，∠C=90°，AB=5，BC=3。求斜边上的高线及中线的长。
-
17、用刻度尺和圆规作一条长度为 的线段。
-
18、 在Rt△ABC中，∠C=Rt∠。(1)、 若AB=5，BC=3，则AC=；(2)、 若 则AB=。
-
19、说出下列命题的逆命题，并判断原命题和逆命题的真假。(1)、直角三角形斜边上的中线等于斜边的一半；(2)、直角三角形只有两个锐角；(3)、有一条边和这条边上的中线对应相等的两个三角形全等。
-
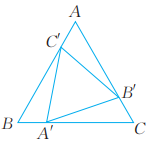
20、已知：如图，点A'，B'，C'分别在等边三角形ABC的三边上，且 求证：△A'B'C'是等边三角形。
