-
1、 在Rt△ABC中，∠C=90°，AB=5，BC=3。求斜边上的高线及中线的长。
-
2、用刻度尺和圆规作一条长度为 的线段。
-
3、 在Rt△ABC中，∠C=Rt∠。(1)、 若AB=5，BC=3，则AC=；(2)、 若 则AB=。
-
4、说出下列命题的逆命题，并判断原命题和逆命题的真假。(1)、直角三角形斜边上的中线等于斜边的一半；(2)、直角三角形只有两个锐角；(3)、有一条边和这条边上的中线对应相等的两个三角形全等。
-
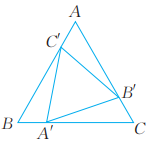
5、已知：如图，点A'，B'，C'分别在等边三角形ABC的三边上，且 求证：△A'B'C'是等边三角形。
-
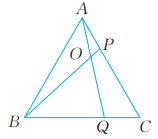
6、 如图，在等边三角形ABC的AC，BC边上各取一点P，Q，使AP=CQ，AQ，BP相交于点O。求∠BOQ的度数。
-
7、已知：如图，O为等边三角形ABC的两条角平分线的交点。求证：
(1)、 OC平分∠ACB。(2)、 OA=OB=OC。 -
8、已知：△ABC的边BC上的中线是△ABC的一条角平分线。求证：△ABC是等腰三角形。
-
9、求证：有两条高线相等的三角形必有两个内角相等。
-
10、 如图，在△ABC中，AC=BC，D，E分别在AB，AC上，且DE∥BC。判断△ADE是不是等腰三角形，并给出证明。
-
11、 已知：如图，AB=AE，∠B=∠E，BC=ED，CF=DF。求证：AF⊥CD。
-
12、已知等腰三角形一个内角的度数为54°，求其余各个内角的度数。
-
13、用两块同样大小的含30°角的直角三角尺拼出等腰三角形。你有多少种不同的方法?分别画出示意图，并说明理由。
-
14、已知等腰三角形的一边长为3，另一边长为6，求它的周长。
-
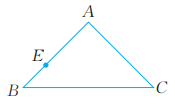
15、如图，在等腰三角形ABC中，AB=AC。先作出它的对称轴，然后作点E的对称点。
-
16、如图所示的图案是一个轴对称图形(不考虑颜色)，直线l是它的一条对称轴。已知圆的半径为r，求绿色部分的面积。
-
17、如图是一幅镶嵌图。该镶嵌图可以由图形F经多次平移和轴对称得到吗?如果你认为可以，简要地描述平移和轴对称过程；否则说明理由。
-
18、如图，直线l1 ， l2 ， l3相交于一点O，每两条直线之间所成的锐角均为60°。
(1)、先以直线l2为对称轴，作与图形Y成轴对称的图形 Y'；再以直线l1为对称轴，作与图形Y'成轴对称的图形Y'”。(2)、以直线l3为对称轴，作与图形Y成轴对称的图形。你发现了什么?(3)、设计一组图形的轴对称，使图形Y最终回到原来的位置，并描述这个过程。 -
19、在图形T上补一个小正方形，使它成为一个轴对称图形，并画出对称轴。你有几种方法?
-
20、如图所示的“天平”是轴对称图形吗?如果是，作出它的对称轴。
