-
1、 命题“x=3是方程 的解”是真命题还是假命题?请说明理由。
-
2、下列命题中，哪些是真命题，哪些是假命题?请说明理由。(1)、同角的补角相等；(2)、一条直线截另外两条直线所得的同位角相等；(3)、有公共顶点且相等的两个角是对顶角；(4)、两个无理数的和仍是无理数。
-
3、 如图，若∠1+∠2=180°，则直线a∥b。 用推理的方法说明它是真命题。
-
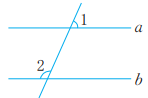
4、列举两个命题，要求其中一个是真命题，另一个是假命题。你是用什么方法来判断它们的真假的?
-
5、判断下列命题的真假，并说明理由。
(1)、 如图①，已知 和 则(2)、两点之间线段最短；(3)、 如图②，若 则(4)、会飞的动物是鸟。 -
6、判断下列命题的真假，并说明理由。(1)、三角形的一条中线将三角形分成面积相等的两部分；(2)、一组对边平行，另一组对边相等的四边形是平行四边形；(3)、 (a为实数)。
-
7、把点A(a，-3)向左平移3个单位长度，所得的点与点A关于y轴对称，求a的值。
-
8、如图，把△ABC平移，使点A平移到点O。作出△ABC平移后所得的△OB'C'，并求△OB'C'的顶点坐标和平移的距离。
-
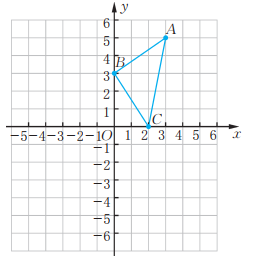
9、如图，分别求一个或一组平移，使：
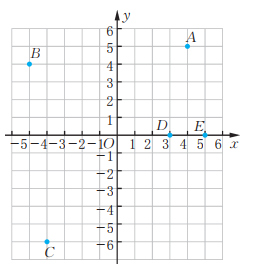(1)、 点D平移到点E；(2)、 点A平移到点C；(3)、 点B平移到点D；(4)、 点(-3，-4)平移到点(1，0)。 -
10、(1)、 把点P(-2，7)向左平移2个单位长度，得点；(2)、 把点P(-2，7)向下平移7个单位长度，得点；(3)、 把以(-2，7)，(-2，-2)为端点的线段向右平移7个单位长度，所得图形上任意一点的坐标可表示为。
-
11、如图，在直角坐标系中，点A的坐标是(1.5，2)。根据下列要求作图。
(1)、把点A向下平移4个单位长度；(2)、把点A向左平移2.5个单位长度；(3)、把直线l向左平移4个单位长度。 -
12、如图，在直角坐标系中有三条线段a，b，c。你能通过平移其中两条线段，使得它们和第三条线段首尾相接组成一个三角形吗?如果能，说出你的平移方法，以及所得三角形三个顶点的坐标。
-
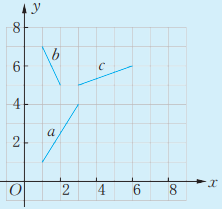
13、把图中图甲平移，使点A移至点O，求点B的对应点的坐标，并画出图甲平移后的图形。
-
14、把点A(-1，3)先向右平移3个单位长度，再向下平移3个单位长度，求最后所得点的坐标。
-
15、如图。
(1)、 分别写出点A，A'和点B，B'的坐标，并比较A与A'，B与B'之间的坐标变化。(2)、图甲怎样平移到图乙? -
16、如图，在直角坐标系中，平行于x轴的线段AB上所有点的纵坐标都是-1，横坐标x的取值范围是1≤x≤5，则线段AB上任意一点的坐标可以用“(x，-1)(1≤x≤5)”表示。按照类似这样的规定，回答下面的问题：
(1)、怎样表示线段CD上任意一点的坐标?(2)、把线段AB向上平移2.5个单位长度，作出所得的线段 线段 上任意一点的坐标怎样表示?(3)、把线段CD向左平移3个单位长度，作出所得的线段 线段C'D'上任意一点的坐标怎样表示? -
17、已知点A的坐标为(a，b)，点A经怎样平移得到下列各点?(1)、 (a-2，b)；(2)、 (a，b+2)。
-
18、已知点A的坐标为(-2，-3)，分别求点A经下列平移后所得的点的坐标。(1)、向上平移3个单位长度；(2)、向下平移3个单位长度；(3)、向左平移2个单位长度；(4)、向右平移4个单位长度。
-
19、《九章算术》中记载了一道有趣的数学题：“今有池方一丈，葭生其中央，出水一尺。引葭赴岸，适与岸齐。问：水深、葭长各几何?”这道题的意思是说：有一个边长为1丈的正方形水池，在池的正中央长着一根芦苇，芦苇露出水面1尺。若将芦苇拉到池边中点处，芦苇的顶端恰好与水面齐平。问：水有多深，芦苇有多长?(1丈=10 尺)请你解决这两个问题。
-
20、 一个屋架的形状如图。已知AC=10m，BC=12m，AC⊥BC，CD⊥AB于点D。求立柱CD的长和点D的位置(结果精确到0.1m)。
