-
1、 如图,在△ABC中,点 D,E分别在边AB,AC上,连接DE,且DE∥BC,若AD=3,AB=4,S四边形DECB=14,则S△ABC= ( )
 A、50 B、40 C、32 D、26
A、50 B、40 C、32 D、26 -
2、如图,在Rt△ABC中, 点D是AB边上的点, 交AC于点E, AB=10,则BC的长为.

-
3、如图,在▱ABCD中,点E 在边AD上,连接BE并延长交CD的延长线于点F,若AE=2ED,DE∥BC则FD:FC的值为.
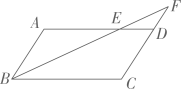
-
4、如图,四边形为正方形,且E 是边延长线上一点,过点B作 于F点, 交于H点, 交于G点, 连接 .
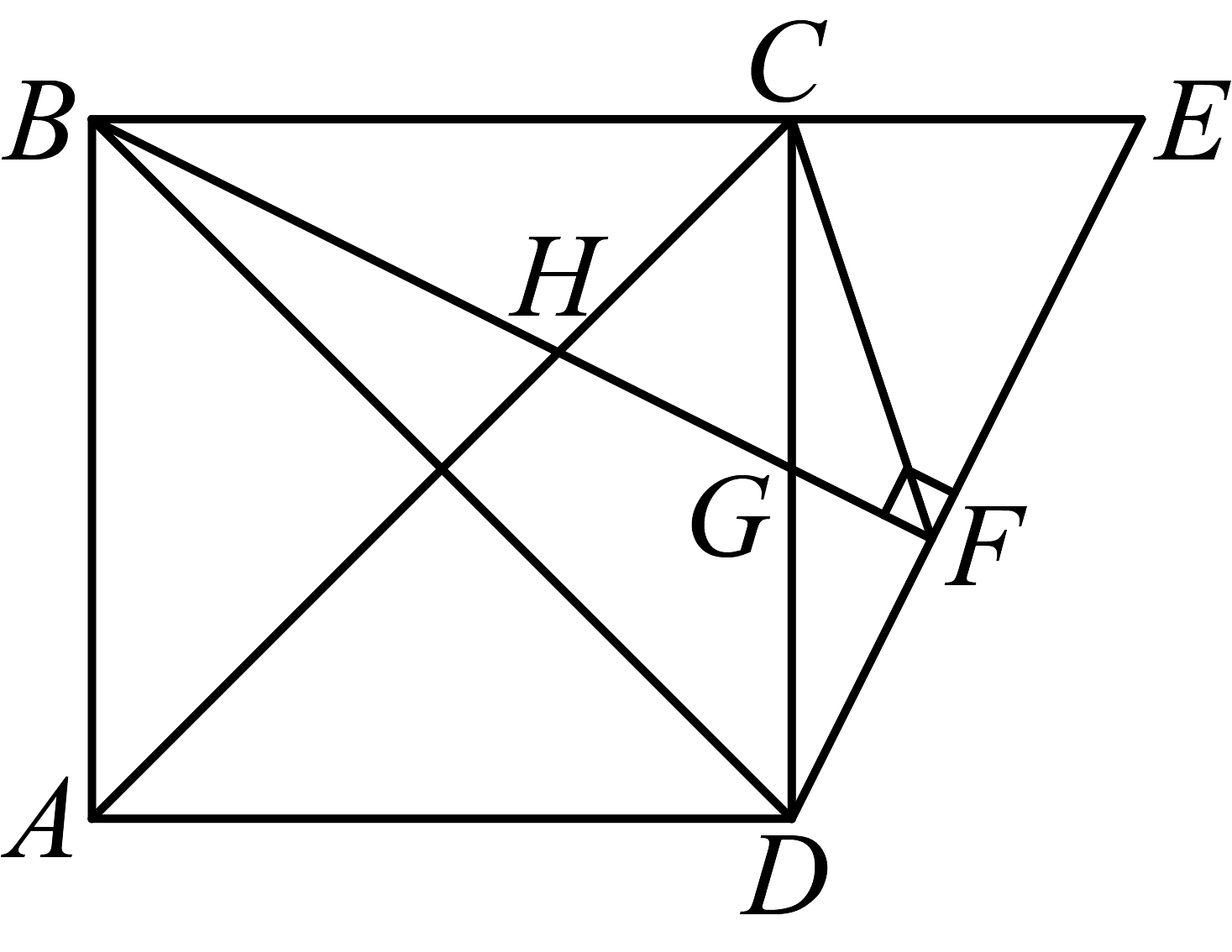 (1)、求证:;(2)、求证:;(3)、求的度数.
(1)、求证:;(2)、求证:;(3)、求的度数. -
5、如图,在平面直角坐标系中,一次函数的图象与反比例函数 的图象交于点 , 与x轴交于点C.
 (1)、求点A 的坐标和反比例函数的解析式;(2)、根据图象直接写出不等式 的解集;(3)、点B是反比例函数图象上一点且纵坐标是1,连接 , 求 的面积.
(1)、求点A 的坐标和反比例函数的解析式;(2)、根据图象直接写出不等式 的解集;(3)、点B是反比例函数图象上一点且纵坐标是1,连接 , 求 的面积. -
6、如图,四边形为菱形,点 E在的延长线上, .
 (1)、求证:;(2)、当 , 时, 求的长.
(1)、求证:;(2)、当 , 时, 求的长. -
7、在综合实践课上,数学兴趣小组用所学数学知识来解决实际问题. 实践报告如下:
实践报告
活动课题
测量河的宽度
活动工具
标杆、卷尺
测量过程
如图,为了测量河的宽度 , 小康所在的数学兴趣小组设计了如下测量方案:

【步骤一】小康站在河岸的点B处立了一根标杆; 小明站河岸的另一端点D处, 立了另一根标杆;
【步骤二】小英适当调整自己所处的位置, 在点A处测得点A, B, D恰好在同一条直线上, 点A, C, E恰好在同一条直线上;
【步骤三】其他同学用卷尺测出标杆及河岸的长;
【步骤四】记录数据 (单位:m)
标杆
1.5
标杆
1.8
河岸
10
解决问题
根据以上数据计算河的宽度.
请你帮助兴趣小组解决以上问题.
-
8、解方程∶(1)、;(2)、 .
-
9、如图, 已知正方形的边长为30, 点E是的中点, 于H,交于G, 则 .

-
10、如图,与是位似图形, 点O为位似中心, . 若 , 则 的长是 .

-
11、如图,是平行四边形,对角线在轴正半轴上,位于第一象限的点和第二象限的点分别在双曲线和的一个分支上,分别过点做轴的垂线段,垂足分别为点和 , 则以下结论:①;②阴影部分面积是;③当时,;④若是菱形,则 . 其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
12、如图, , 若 , 则为( )
 A、3 B、4 C、8 D、9
A、3 B、4 C、8 D、9 -
13、如图,已知 , 若 , 则的长为( )
 A、4 B、4.5 C、5.5 D、6
A、4 B、4.5 C、5.5 D、6 -
14、利用公式法解得一元二次方程的两个根为 , 且 , 则的值为( )A、 B、 C、 D、
-
15、九年级学生小林进行跨学科自主学习活动,他利用函数的相关知识在实验场景和实验场景下做对比,研究某种化学试剂的挥发情况,若当实验过程中该试剂挥发时间为分钟时,在实验场景 , 中的剩余质量分别为 , (单位:克)记录 , 与的几组对应值如下:
(分钟)
0
5
10
15
20
…
(克)
25
23.5
20
14.5
7
…
(克)
25
20
15
10
5
…
请你协助小林将探究过程补充完整:
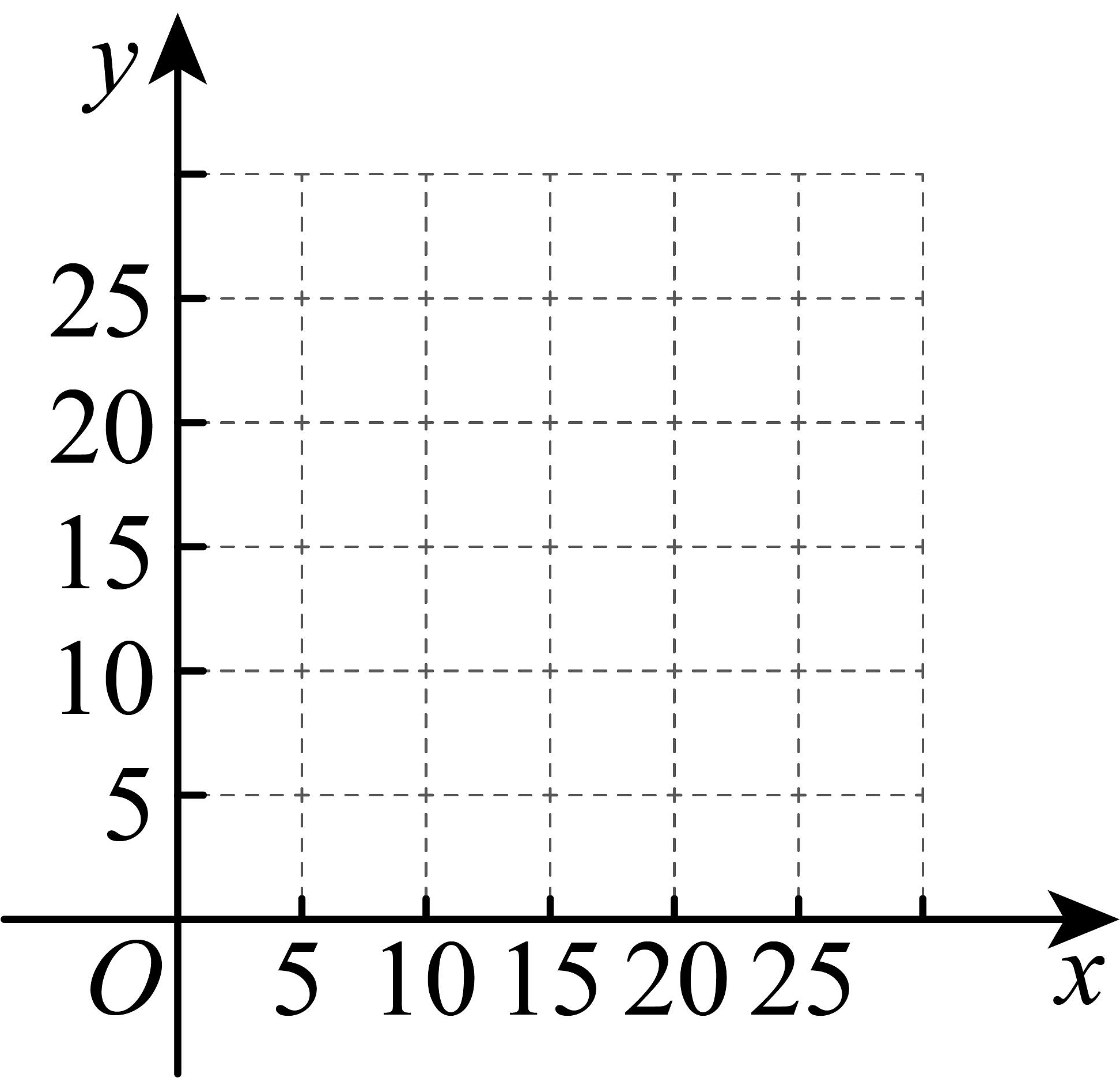 (1)、在同一平面直角坐标系中,描出上表中各组数值所对应的点 , 并画出函数 , 的图象;(2)、进一步探究发现,实验场景的图象是抛物线的一部分,与之间近似满足二次函数:;实验场景的图象是直线的一部分,与之间近似满足一次函数 , 则___________,___________,___________;(3)、查阅文献可知,该化学试剂的质量不低于5克时,才能发挥有效作用,在上述实验中,记该化学试剂在场景 , 中发挥有效作用的时间分别为 , , 则___________(填“>”,“=”或“<”).
(1)、在同一平面直角坐标系中,描出上表中各组数值所对应的点 , 并画出函数 , 的图象;(2)、进一步探究发现,实验场景的图象是抛物线的一部分,与之间近似满足二次函数:;实验场景的图象是直线的一部分,与之间近似满足一次函数 , 则___________,___________,___________;(3)、查阅文献可知,该化学试剂的质量不低于5克时,才能发挥有效作用,在上述实验中,记该化学试剂在场景 , 中发挥有效作用的时间分别为 , , 则___________(填“>”,“=”或“<”). -
16、已知抛物线(是常数)(1)、当时,求该抛物线的顶点坐标;(2)、证明:不论为何值,该抛物线与轴没有交点.
-
17、在平面直角坐标系中,的三个顶点坐标分别为 , , .
 (1)、画出关于轴对称的;(2)、以原点为位似中心,在网格中画出(1)中的位似图形 , 使与的相似比为 .
(1)、画出关于轴对称的;(2)、以原点为位似中心,在网格中画出(1)中的位似图形 , 使与的相似比为 . -
18、如图,抛物线(b,c是常数)与x轴负半轴、y轴负半轴分别交于点A和点B,已知 . 求 , 的值.
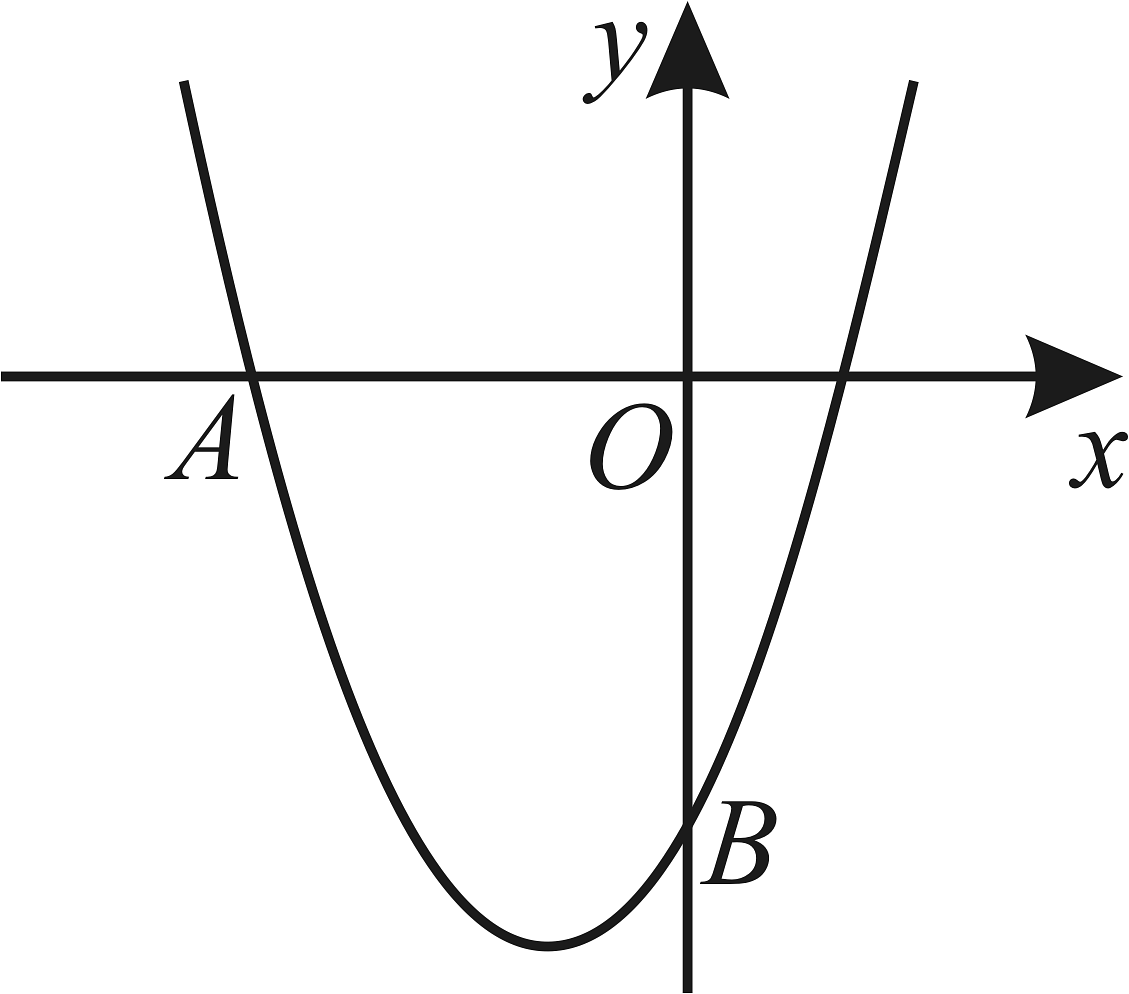
-
19、如图,某公园的示意图是对角线互相垂直的四边形 , 已知米,则该四边形公园的最大面积为平方米.

-
20、如图,已知 , 补充一个条件: , 可使 .
