-
1、 如图，在正方形ABCD中，点E，F分别在边CD，AD 上，BE⊥CF于点G，若BC=8，AF=2，则GF的长为.
-
2、如图，在正方形ABCD中，E，F分别为边BC，CD的中点，连结AE，BF交于点P，连结CP 并延长，交 AB 于点Q.
求证：
(1)、PC平分∠EPF；(2)、AQ=2BQ. -
3、如图，在正方形ABCD中，E，F分别为边BC，CD的中点，连结 AE，BF交于点 P，连结 PD.求证：
(1)、AE⊥BF；(2)、PD=AB. -
4、已知：如图，在正方形ABCD中，E，F 分别是BC，CD 上的点，AE⊥BF.求证：AE=BF.
-
5、 如图
【感知】如图①，在▱ABCD中，对角线 AC，BD 相交于点O，过点O的直线EF 分别交边 AB，CD 于点E，F.易证：△BOE≌△DOF（不需要证明）.
【探究】若图①中的直线 EF 分别交边 CB，AD的延长线于点H，G，其他条件不变，如图②.求证：△BOH≌△DOG；
【应用】在图②中，连结 AH.若∠ADB=90°，AB=10，AD=6，BH= BC，求 GH 的长和四边形AHBD 的面积.
-
6、 如图，在▱ABCD 中，过对角线 AC的中点 O作直线 EF 交边 AB，CD于点E，F.
(1)、求证：AE=CF；(2)、若EF⊥AC，AC=8，cos∠BAC=0.8，连结AF，CE，求四边形AECF 的面积. -
7、 如图， □ABCD的对角线AC，BD相交于点O，E 为边 BC 的中点，连结 EO 并延长交边AD 于点F，∠ABC=60°，BC=2AB.下列结论错误的是（ ）
A、AB⊥AC B、AD=4OE C、四边形 AECF 为菱形 D、 -
8、 如图，O是菱形ABCD 的对称中心，连结OA，OB，OA=4，OB=6，EF为过点O 的一条直线，点E，F分别在AD，BC上，则图中阴影部分的面积为（ ）
A、24 B、16 C、18 D、12 -
9、如图5，在□ABCD 中，AB⊥AC，AB=1，BC= 对角线AC，BD 相交于点O，将直线 AC 绕点 O 顺时针旋转，分别交 BC，AD于点E，F.
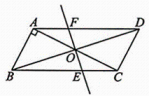(1)、【问题解决】求证：当旋转角为90°时，四边形ABEF是平行四边形.
(2)、【类比探究】试说明在旋转过程中，线段 AF 与EC 总保持相等.
(3)、【拓展应用】在旋转过程中，四边形BEDF 可能是菱形吗?如果不可能，请说明理由；如果可能，请证明并求出此时AC绕点O 顺时针旋转的度数.
-
10、如图， □ABCD 的对角线AC，BD 相交于点O，EF 过点O 且分别与AB，CD交于点E，F，连结 EC.
(1)、求证：OE=OF；(2)、若EF⊥AC，△BEC的周长是10，求□ABCD的周长. -
11、如图，EF过▱ABCD 对角线的交点O，交AD 于点E，交 BC于点 F，有下列结论：①AE=CF；②若AB=4，AC=6，则 2<BD<14；③S△AOB = S□ABCD；（；④S四边形ABFE=S△ABC.其中正确的结论是.（只填序号）
-
12、已知：如图， ▱ABCD的对角线AC，BD交于点O.过点O作直线EF，分别交AB，CD于点E，F.求证：OE=OF.
-
13、已知正方形 ABCD，E 是对角线 AC 上一点.
(1)、 如图①，连结 BE， DE，求证：△ABE≌△ADE；(2)、如图②，F 是 DE 延长线上一点，DF 交AB 于点G，BF⊥BE.判断△FBG的形状，并说明理由；(3)、在（2）的条件下，若BE=BF=2，求 的值. -
14、 如图，在▱ABCD中，对角线AC，BD相交于点O，∠ABC=90°.
(1)、求证：AC=BD；(2)、点 E 在 BC 边上，满足∠CEO=∠COE.若AB=6，BC=8，求 CE 的长及 tan∠CEO的值. -
15、如图，矩形 ABCD 的对角线 AC与 BD 相交于点 O，OE∥CD，直线CE是线段 OD 的垂直平分线，CE 分别交 OD，AD 于点 F，G，连结 DE.
(1)、判断四边形OCDE 的形状，并说明理由；(2)、当CD=4时，求 EG的长. -
16、如图，在 Rt△ABC中，∠BAC=90°，D 是 BC 的中点，E 是 AD 的中点，过点 A 作AF∥BC交CE的延长线于点F，连结BF.
(1)、求证：四边形ADBF是菱形；(2)、若AB=8，四边形ADBF的面积为32 点 M 在线段BC 上，AM=7，求 BM的长. -
17、如图，在菱形 ABCD 中，点 O为对称中心，点E 从点 A出发沿 AB 向点 B 移动，移动到点 B 停止，作射线EO，交边CD 于点 F，则四边形 AECF 形状的变化依次为 （ ）
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→矩形→平行四边形→菱形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形 -
18、如图，DF，EF是△ABC的两条中位线.我们探究的问题是：这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的边或角有什么关系?建议按下列步骤探索：
(1)、围成的四边形是否必定是平行四边形?(2)、在什么条件下，围成的四边形是菱形?(3)、在什么条件下，围成的四边形是矩形?(4)、你还能发现其他什么结论吗? -
19、 如图，E，F，G，H 分别是四边形ABCD的边AB，BC，CD，DA的中点，则下列说法中正确的个数是（ ）
①若 AC=BD，则四边形EFGH 为矩形；②若 AC⊥BD，则四边形EFGH 为菱形；③若四边形 EFGH 是平行四边形，则AC与BD 互相平分；④若四边形 EFGH 是正方形，则 AC 与 BD互相垂直且相等.
A、1 B、2 C、3 D、4 -
20、小明在学习“特殊平行四边形”一单元后，梳理了如图所示的特殊平行四边形之间的关系.以下选项分别表示A，B，C，D处填写的内容，则对应位置填写错误的选项是 （ ）
A、对角线的夹角为60° B、对角线互相垂直 C、对角线与一边的夹角为45° D、对角线相等