-
1、 定义:对于y关于x的函数,函数在 范围内的最大值,记作M[x1 , x2].
如函数y=2x,在-1≤x≤3范围内,该函数的最大值是6,即M[-1,3]=6.
请根据以上信息,完成以下问题:
已知函数 (a为常数).
(1)、若a=2.①直接写出该函数的表达式,并求 M[1,4]的值;
②已知 求p的值.
(2)、若该函数的图象经过点(0,0),且.M[-3,k]=k,求k的值. -
2、 在数轴上,点A表示的数是4,点O表示的数是0,点 P 表示的数是p(p≠0).定义:点 B在线段OP 上,如果线段 AB的长度有最大值m,则称m为点 A与线段OP的“闭距离”.例如:p=2,当点 B 与点 O重合时,m=4.若p=-2,则m的值是( )A、2 B、4 C、5 D、6
-
3、 对于一个二次函数 y=a(x- 中存在一点 P(x',y'),使得x'- 则称 为该抛物线的“开口大小”,那么抛物线 的“开口大小”为.
-
4、 如图 R4-12,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系.
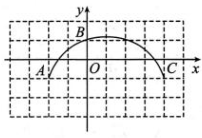 (1)、过点 A,B,C的圆的圆心M 的坐标为;(2)、请通过计算判断点 D(-3,-2)与⊙M的位置关系.
(1)、过点 A,B,C的圆的圆心M 的坐标为;(2)、请通过计算判断点 D(-3,-2)与⊙M的位置关系. -
5、 如图,点 A 是 5×5 网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1,以点 A 为其中的一个顶点,面积等于 的格点等腰直角三角形(三角形的三个顶点都是格点)的个数为( )
 A、10个 B、12个 C、14 个 D、16个
A、10个 B、12个 C、14 个 D、16个 -
6、 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点 C,D,则cos∠ADC的值为.
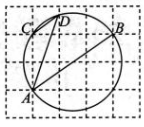
-
7、 如图 是由边长为1的小正方形组成的3×3网格,△ABC的顶点均在格点上.按如下要求利用无刻度的直尺作图(保留作图痕迹,不写作法).
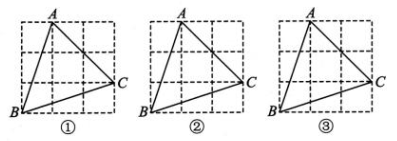 (1)、如图①,画出△ABC的中线AD;(2)、如图②,在△ABC的边 BC 上找一点E,使得∠BAE=45°;(3)、如图③,在△ABC的边 BC 上找一点 F,连结 AF,使△ABF的面积为 1.
(1)、如图①,画出△ABC的中线AD;(2)、如图②,在△ABC的边 BC 上找一点E,使得∠BAE=45°;(3)、如图③,在△ABC的边 BC 上找一点 F,连结 AF,使△ABF的面积为 1. -
8、 如图,在5×5的方格纸中,请按要求画格点图形(顶点均在格点上).
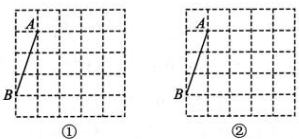 (1)、在图①中画一个△ABC,使点 C在AB 的中垂线上;(2)、在图②中画一个△ABC,使点 B 在AC 的中垂线上.
(1)、在图①中画一个△ABC,使点 C在AB 的中垂线上;(2)、在图②中画一个△ABC,使点 B 在AC 的中垂线上. -
9、 如图,在由边长为1的小正方形构成的5×6的网格中,△ABC的顶点A,B,C均在格点上.请按要求完成作图:①仅用无刻度直尺;②保留作图痕迹并标注相关字母.
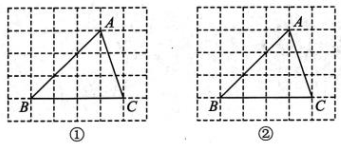 (1)、如图①,在△ABC内寻找格点 P,使得∠BPC=2∠A;(2)、如图②,在线段AC上找一点 Q,使得
(1)、如图①,在△ABC内寻找格点 P,使得∠BPC=2∠A;(2)、如图②,在线段AC上找一点 Q,使得 -
10、 如图,各图形顶点都在小正方形的格点上,分别根据下列要求画出图形.
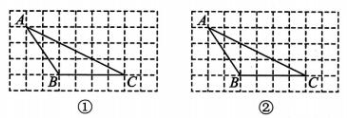 (1)、在图①中,在BC上找一点D,使得AD平分△ABC的面积;(2)、在图②中,在 BC上找一点E,使得AE 将△ABC分成面积比为1:2 的两部分.(找到一个即可)
(1)、在图①中,在BC上找一点D,使得AD平分△ABC的面积;(2)、在图②中,在 BC上找一点E,使得AE 将△ABC分成面积比为1:2 的两部分.(找到一个即可) -
11、 图①②都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,分别按要求在网格内画出格点图形(顶点均在格点上).
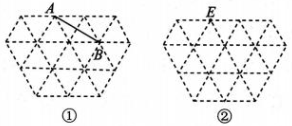 (1)、在图①中以 AB为对角线画一个四边形ADBC,使得AB=CD;(2)、在图②中以点 E 为顶点画一个菱形EF-GH,使得S菱形EFGH=2S四边形ADBC ,
(1)、在图①中以 AB为对角线画一个四边形ADBC,使得AB=CD;(2)、在图②中以点 E 为顶点画一个菱形EF-GH,使得S菱形EFGH=2S四边形ADBC , -
12、 图①②都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段 AB 的端点均在格点上,分别按要求画出图形.
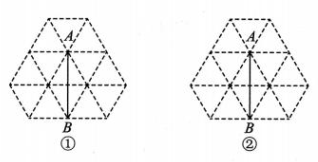 (1)、在图①中画出一个以 AB 为边的▱AB-CD,且点 C 和点 D 均在格点上;(2)、在图②中画出一个以 AB 为对角线的菱形AEBF,且点 E 和点 F 均在格点上.
(1)、在图①中画出一个以 AB 为边的▱AB-CD,且点 C 和点 D 均在格点上;(2)、在图②中画出一个以 AB 为对角线的菱形AEBF,且点 E 和点 F 均在格点上. -
13、如图,在四边形ABCD 中,AB∥CD,点 E 在边 AB上, ▲ .
请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
 (1)、求证:四边形 BCDE为平行四边形;(2)、若AD⊥AB,AD=8,BC=10,求线段AE的长.
(1)、求证:四边形 BCDE为平行四边形;(2)、若AD⊥AB,AD=8,BC=10,求线段AE的长. -
14、一次函数y=(3m+1)x-2 的值随x的增大而增大,请写出一个满足条件的m的值:.
-
15、 阅读材料:小学阶段我们学习过被3整除的数的规律,初中阶段可以论证结论的正确性.以三位数为例,设abc是一个三位数,若a+b+c可以被3整除,则这个数可以被3 整除.论证过程如下: abc=100a+10b+c=(99a+9b)+(a+b+c),显然99a+9b可以被3整除,因此,如果a+b+c可以被3整除,那么 abc就能被3整除.
应用材料解答下列问题:
(1)、设是一个三位数,当满足什么条件时,它可以被5 整除?(2)、设是一个四位数,猜想满足什么条件时,它可以被4整除,并说明理由. -
16、 已知a,b,c为非零实数,且满足a+b+c=0,4a+2b+c<2,则下列结论一定正确的是( )A、2a-c>2 B、3a-b-3c<4 C、3a<2 D、a+3b+4c>0
-
17、已知点 P(4t,m), 都在反比例函数 的图象上,则下列结论中一定正确的是 ( )A、m+n>0 B、m+n<0 C、|m|>n D、|m|<n
-
18、“字母表示数”的系统化阐述是 16 世纪提出的,被后人称为从“算术”到“代数”的一次飞跃,从而大大推动了数学的发展.经过初中数学的学习,我们知道了用字母表示数可以分析从特殊到一般的数学规律,字母与数一样,也可以参与运算.请同学们观察下列关于正整数的平方拆分的等式:
第 1个等式:
第2个等式:
第3个等式:
第 4 个等式:
(1)、请用此方法拆分 20242;(2)、请你用上面的规律归纳出一个一般的结论(用含n的等式表示,n为正整数),并运用有关知识说明这个结论是正确的. -
19、 观察前后两个差为4 的整数的平方差:
①52-12=8×3;②62-22=8×4;( 8×5;….
(1)、写出第n个等式,并进行证明.(2)、2024是否可以写成两个差为4 的整数的平方差?如果可以,请写出这两个整数;如果不可以,请说明理由. -
20、 一组有序排列的数具有如下规律:任意相邻的三个数,中间的数等于前后两数的积.若这组数第1个数是a,第5个数是 , 则第2028 个数是(用含 a 的式子表示).