-
1、某旅游景点的门票收费标准是每人30元.某公司计划组织员工去该景点旅游,写出总门票费用y(元)与员工人数x(人)之间的关系式,并判断y是不是x的正比例函数.
-
2、已知 是关于x的正比例函数,当x=-4时,y的值为.
-
3、下列各选项中,两个变量y与x之间的关系是正比例函数关系的是( )A、直角三角形中一个锐角的度数y(度)与另一个锐角的度数x(度)之间的关系 B、正方体的表面积y(cm2)与它的棱长x(cm)之间的关系 C、小红阅读一本420 页的名著,未读的页数y(页)与已读的页数x(页)之间的关系 D、汽车以60 km/h 的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系
-
4、列函数,其中y是x的正比例函数的个数是( )
①y=x-3;②y= ;③y= kx;④y=;⑤y=;⑥y 2y.
A、3 B、4 C、5 D、6 -
5、根据如图所示的程序计算函数y的值,当输入x的值为4时,输出的y值为7,当输入x的值为2时,输出的y值为.

-
6、据史书记载,漏刻是中国古代的一种计时工具,是古代人民对函数思想的创造性应用.研究发现水位h(cm)与时间t(min)满足h=0.4t+2,当h为6时,时间t的值为( )A、4.4 B、10 C、15 D、20
-
7、当x=-1时,函数y= 的值是( )A、1 B、-1 C、 D、
-
8、在标准大气压下,温度达到100℃水就会沸腾,下表是某同学记录的水的温度 T(℃)和烧水的时间t(min)的数据.
t(min)
0
2
4
6
8
10
12
14
…
T(℃)
30
44
58
72
86
100
100
100
…
下列说法不正确的是( )
A、t是自变量,T是因变量 B、在水沸腾之前,烧水的时间每增加 1m in,水的温度上升7 ℃ C、烧水10 min时,水达到沸腾状态 D、T与t之间的关系式为T=7t+30 -
9、均匀地向一个容器内注水,在注满水的过程中,水面的高度 h与时间t的函数关系如图所示,则这个容器的形状可以是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
10、下列不能表示y是x的函数的是( )A、
B、y=2x+1 C、y=±6x D、x
0
5
10
15
y
3
3.5
4
4.5

-
11、下列各图中,表示在某一变化过程中变量y是变量x的函数的是( )A、
 B、
B、 C、
C、 D、
D、
-
12、有下面六个关系式:①y=|x|;②|y|=x;③2x2-y=0;④y= (x≥0);⑤y= ;⑥y2=3x.其中y是x的函数的是( )A、①②④⑤ B、②③⑤⑥ C、①②③⑥ D、①③④⑤
-
13、在平面直角坐标系中,线段AB的端点坐标分别为A(2,-1),B(1,0),将线段AB 平移后,点A 的对应点 A'的坐标为(2,1),则点 B 的对应点 B'的坐标为.
-
14、平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3 所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移),每次平移1个单位长度.

若“和点”Q按上述规则连续平移16次后,到达点(Q16(-1,9),则点Q的坐标为( )
A、(6,1)或(7,1) B、(15,-7)或(8,0) C、(6,0)或(8,0) D、(5,1)或(7,1) -
15、不等式2x+4≥3x+2的解集在数轴上表示正确的是 ( )A、
 B、
B、 C、
C、 D、
D、
-
16、定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
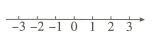 (1)、求(-2)⊕3的值;(2)、若1⊕x的值小于3,求x的取值范围,并在数轴上表示出来.
(1)、求(-2)⊕3的值;(2)、若1⊕x的值小于3,求x的取值范围,并在数轴上表示出来. -
17、解下列不等式并把它们的解集在数轴上表示出来:(1)、2x-1<3x+2;(2)、x-1>5x-6.
-
18、已知关于x的不等式x-a≤-2的解集表示在数轴上如图所示,那么a的值是.

-
19、解集是 的不等式是( )A、2+2x<3 B、5x-2<-9 C、 D、2x<3x+1
-
20、已知下列表格中的每组x,y的值分别是关于x,y 的二元一次方程 ax+b=y的解,则关于x的不等式 ax+b>0的解集为( )
x
…
-3
-2
-1
0
1
…
y
… -1
0
1
2
3
… A、x>-2 B、x<-2 C、x<0 D、x>0