相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、已知则的值为( )A、-1 B、2 C、-3 D、4
-
2、某服装厂生产一种西装和领带,西装每套定价300元,领带每条定价60元,厂方在开展促销活动中,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条 .
(1)、若该客户按方案①购买,需付款_____元(用含x的代数式表示);若该客户按方案②购买,需付款______元(用含x的代数式表示);(2)、若 , 通过计算说明此时按哪种方案购买较为合算? -
3、观察下面的点阵图和相应的等式,探究其中的规律:(1)、认真观察,并在后面的横线上写出相应的等式.
 (2)、结合(1)观察下列点阵图,并在后面的横线上写出相应的等式.
(2)、结合(1)观察下列点阵图,并在后面的横线上写出相应的等式. (3)、通过猜想,写出(2)中与第个点阵相对应的等式 .
(3)、通过猜想,写出(2)中与第个点阵相对应的等式 . -
4、在学完解一元一次方程后,聪明的小明同学解方程的过程如下:
解:原方程可变形为 ,
去分母,得 ,
去括号,得 ,
移项、合并同类项,得 .
参考小明的解题过程,解方程: .
-
5、若互为相反数,c、d互为倒数,m为最小的正整数,求代数式 .
-
6、把下列各数填在相应的括号里:
, , , 4,0, , ,
(1)、整数:{ …};(2)、负整数:{ …};(3)、分数:{ …};(4)、非负数:{ …}. -
7、为确保信息安全,信息需加密传输,发送方由明文密文(加密);接收方由密文明文(解密).已知加密规则为:明文 , , , , 对应密文 , , , , 当接收方收到密文 , , , 时,解密得到明文 , , , , 则 .
-
8、一个两位数,个位数字与十位数字之和是10,个位数字为x,用代数式表示这个两位数是 .
-
9、方程去分母后得( )A、3 (x-3) =1- (1+2x) B、3 (x-3) =6- 1+2x C、3 (x-3) =1-1-2x D、3 (x-3) =6- (1+2x)
-
10、下列说法正确的是( )A、近似数3.6万精确到十分位 B、近似数0.720精确到百分位 C、近似数5.78精确到百分位 D、近似数3000精确到千位
-
11、如图,根据有理数a,b,c在数轴上的位置,下列关系正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、若a是有理数,则下列说法正确的是( )A、一定是正数 B、一定是正数 C、一定是负数 D、一定是正数
-
13、如图,四边形为正方形,且E 是边延长线上一点,过点B作 于F点, 交于H点, 交于G点, 连接 .
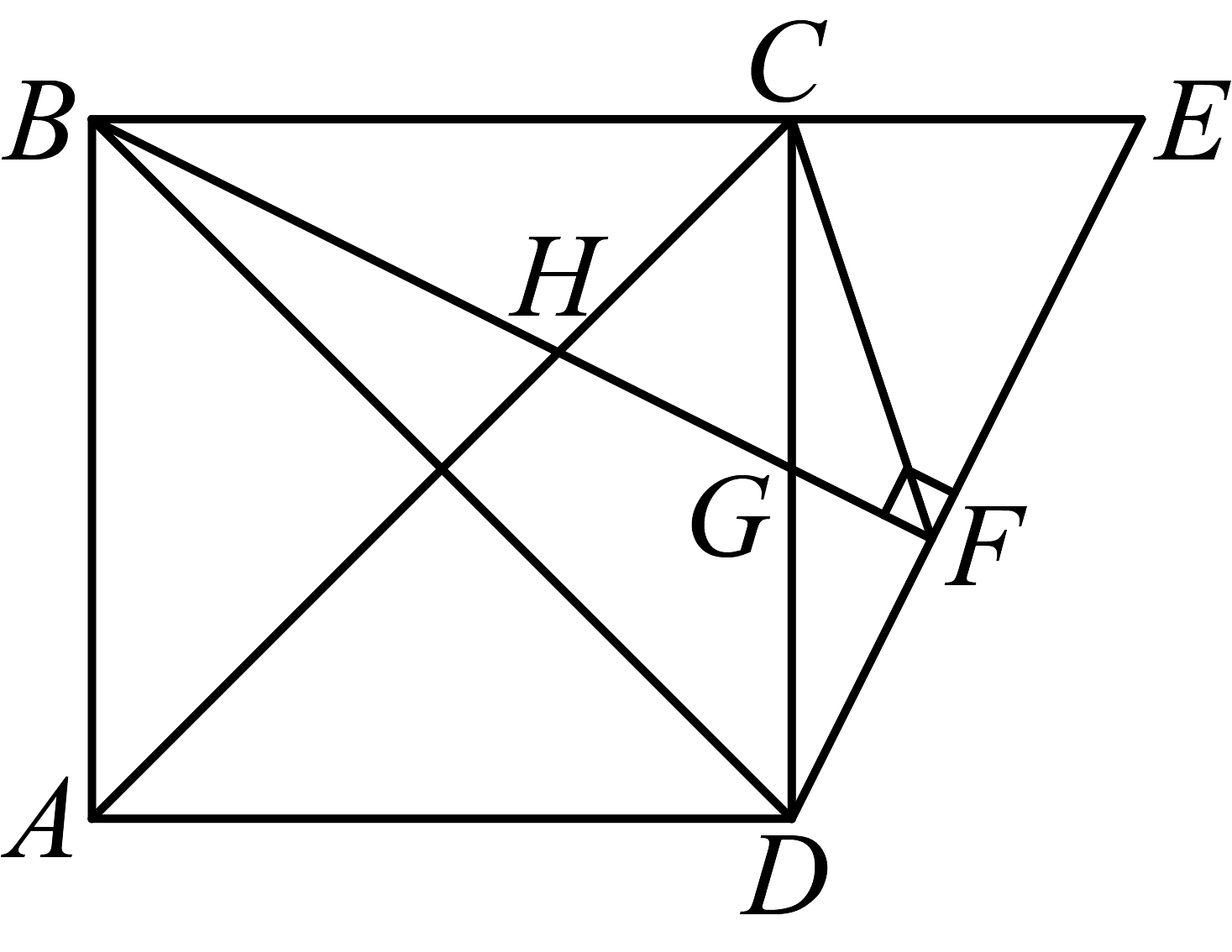 (1)、求证:;(2)、求证:;(3)、求的度数.
(1)、求证:;(2)、求证:;(3)、求的度数. -
14、如图,在平面直角坐标系中,一次函数的图象与反比例函数 的图象交于点 , 与x轴交于点C.
 (1)、求点A 的坐标和反比例函数的解析式;(2)、根据图象直接写出不等式 的解集;(3)、点B是反比例函数图象上一点且纵坐标是1,连接 , 求 的面积.
(1)、求点A 的坐标和反比例函数的解析式;(2)、根据图象直接写出不等式 的解集;(3)、点B是反比例函数图象上一点且纵坐标是1,连接 , 求 的面积. -
15、如图,四边形为菱形,点 E在的延长线上, .
 (1)、求证:;(2)、当 , 时, 求的长.
(1)、求证:;(2)、当 , 时, 求的长. -
16、在综合实践课上,数学兴趣小组用所学数学知识来解决实际问题. 实践报告如下:
实践报告
活动课题
测量河的宽度
活动工具
标杆、卷尺
测量过程
如图,为了测量河的宽度 , 小康所在的数学兴趣小组设计了如下测量方案:

【步骤一】小康站在河岸的点B处立了一根标杆; 小明站河岸的另一端点D处, 立了另一根标杆;
【步骤二】小英适当调整自己所处的位置, 在点A处测得点A, B, D恰好在同一条直线上, 点A, C, E恰好在同一条直线上;
【步骤三】其他同学用卷尺测出标杆及河岸的长;
【步骤四】记录数据 (单位:m)
标杆
1.5
标杆
1.8
河岸
10
解决问题
根据以上数据计算河的宽度.
请你帮助兴趣小组解决以上问题.
-
17、解方程∶(1)、;(2)、 .
-
18、如图, 已知正方形的边长为30, 点E是的中点, 于H,交于G, 则 .

-
19、如图,与是位似图形, 点O为位似中心, . 若 , 则 的长是 .

-
20、如图,是平行四边形,对角线在轴正半轴上,位于第一象限的点和第二象限的点分别在双曲线和的一个分支上,分别过点做轴的垂线段,垂足分别为点和 , 则以下结论:①;②阴影部分面积是;③当时,;④若是菱形,则 . 其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个