相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、为估计池塘两岸、间的距离,如图,小明在池塘一侧选取了一点 , 测得 , , 那么的距离不可能是( )
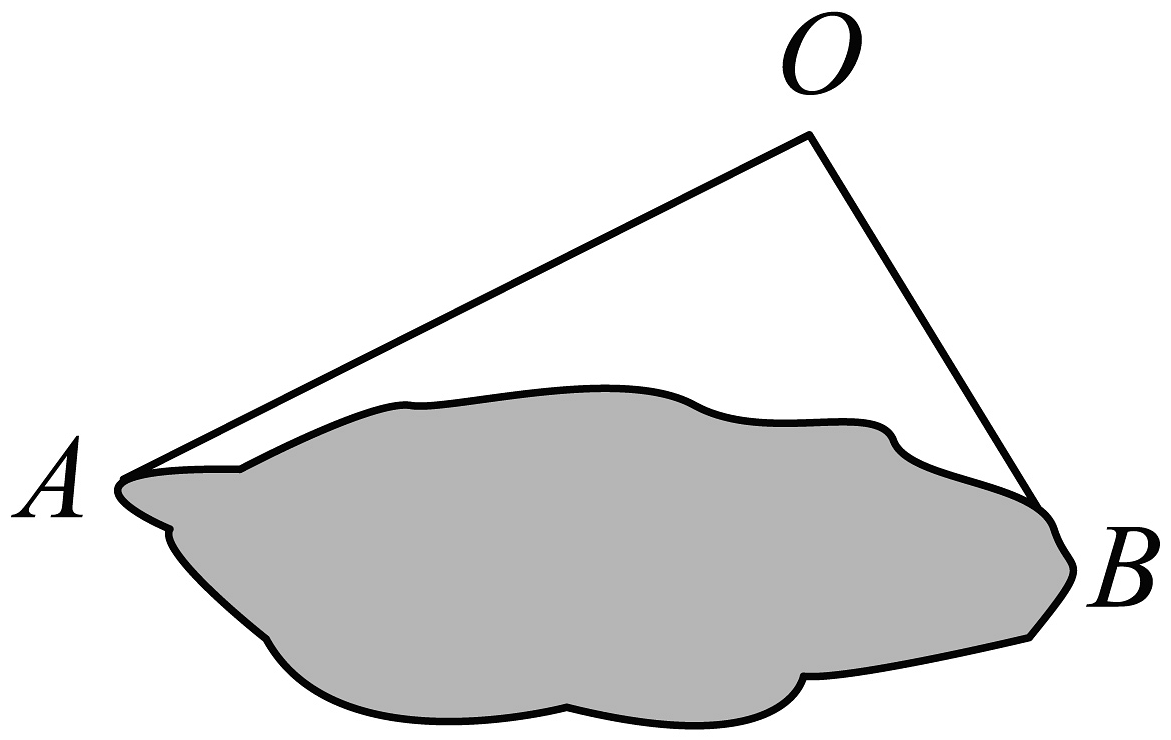 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图,在中, , 点D在线段上, , 垂足为E,则的边上的高是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、两个小组同时开始攀登一座 450m高的山,第一组的平均登高速度是第二组的1.2倍,他们比第二组早15 min到达顶峰.两个小组的平均登高速度各是多少?如果山高为 hm,第一组的平均登高速度是第二组的a倍,并比第二组早 t min 到达顶峰,那么两组的平均登高速度各是多少?
-
4、改良玉米品种后,迎春村玉米平均每公顷增加产量at,原来产 mt玉米的一块土地,现在的总产量增加了20 t.原来和现在平均每公顷玉米的产量各是多少?
-
5、一个圆柱形容器的容积为V m3 , 开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水,向容器中注满水的全过程共用时t min.求两根水管各自的注水速度.(提示:要考虑大水管的注水速度是小水管注水速度的多少倍.)
-
6、王芳3h清点完一批图书的一半,刘伟加入清点另一半图书的工作,两人合作1.2h清点完另一半图书.刘伟单独清点这批图书需要几小时?
-
7、 A,B两种机器都被用来搬运化工原料,A型机器比 B型机器每小时多搬运30kg,A型机器搬运900kg所用时间与B型机器搬运600kg所用时间相等,两种机器每小时分别搬运多少化工原料?
-
8、甲、乙两人分别从距目的地6km和10km的两地同时出发,甲、乙的平均速度比是3:4,结果甲比乙提前20 min到达目的地.求甲、乙的平均速度.
-
9、解下列关于x的方程:(1)、(2)、且m≠1).
-
10、解下列方程:(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、
-
11、甲、 乙两人做某种机械零件.已知甲每小时比乙多做6个, 甲做90个所用的时间与乙做60个所用的时间相等.求甲、乙每小时各做零件多少个.
-
12、八年级学生去距学校 30 km的中国人民抗日战争纪念馆参观,一部分学生乘大巴先出发,过了5 min,其余学生乘中巴出发,结果他们同时到达.已知中巴的平均速度是大巴平均速度的1.2倍, 求大巴的平均速度.

-
13、某次列车平均提速v km/h.在相同的时间内,列车提速前行驶s km,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
-
14、两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 , 这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
-
15、解下列方程:(1)、(2)、(3)、(4)、(5)、(6)、
-
16、解方程
-
17、某种产品的原料提价,因而厂家决定对产品进行提价,现有三种方案:(1)、第一次提价 p%,第二次提价q%;(2)第一次提价q%,第二次提价 p%;(3)第一、二次提价均为 其中p,q是不相等的正数.三种方案哪种提价最多?
(提示:因为 所以
-
18、 已知x"=64, x"=8,求 的值.
-
19、如图是一水压机空心钢立柱的示意图.如果其高h 为 18 m,外径D为1m,内径d 为0.4m ,每立方米钢的质量为7.8t,求该立柱的质量.(π取3.14,结果保留小数点后两位.)

-
20、一张正方形纸片的边长减少 2cm ,它的面积就减少 20 cm2 , 这张正方形纸片的边长是多少?