相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、 , 两数在数轴上对应点的位置如图所示,下列结论中正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2、褐马鸡是我国的珍稀鸟类,如图是保护褐马鸡宣传牌上利用网格画出的褐马鸡的示意图.若建立适当的平面直角坐标系,表示嘴部点的坐标为 , 表示尾部点的坐标为 , 则表示足部点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、已知抛物线与轴交于 , 两点,与轴交于点C.
 (1)、求抛物线的解析式;(2)、如图(1),为抛物线上第一象限内一点,若 , 求点的坐标;(3)、如图(2),为轴上方一动点,直线与抛物线均只有唯一公共点 , 于点 , 且的面积是10,求线段长度的最大值.
(1)、求抛物线的解析式;(2)、如图(1),为抛物线上第一象限内一点,若 , 求点的坐标;(3)、如图(2),为轴上方一动点,直线与抛物线均只有唯一公共点 , 于点 , 且的面积是10,求线段长度的最大值. -
4、如图,在中, , , 点为内一点.
 (1)、如图(1), , , 连接 , 求证:;(2)、如图(2),为的中点,若 , , , 求线段的长;(3)、如图(3),在(2)的条件下,若点为平面内一点, , 连 , 将线段绕点顺时针旋转至 , 连 , 请直接写出的最大值.
(1)、如图(1), , , 连接 , 求证:;(2)、如图(2),为的中点,若 , , , 求线段的长;(3)、如图(3),在(2)的条件下,若点为平面内一点, , 连 , 将线段绕点顺时针旋转至 , 连 , 请直接写出的最大值. -
5、如图是由小正方形组成的的网格,小正方形的顶点称为格点, , , , , 五个点均为格点,是线段与网格线的交点,仅用无刻度的直尺在给定网格中完成画图,每个画图任务的画线不得超过三条.
 (1)、在图(1)中,若点和关于点中心对称,画点;(2)、在图(1)中,若点绕点逆时针旋转后得到点 , 画点;(3)、在图(2)中,在线段上画点 , 使;(4)、在图(2)中,画满足条件的格点 , 使 .
(1)、在图(1)中,若点和关于点中心对称,画点;(2)、在图(1)中,若点绕点逆时针旋转后得到点 , 画点;(3)、在图(2)中,在线段上画点 , 使;(4)、在图(2)中,画满足条件的格点 , 使 . -
6、如图,已知直线交于两点,为的直径,为上一点,平分 , 过点作于点 .
 (1)、求证:为的切线;(2)、若已知的半径为5,且 , 求的长.
(1)、求证:为的切线;(2)、若已知的半径为5,且 , 求的长. -
7、二次函数中的的部分取值如下表:根据表中数据填空:
x
…
0
1
2
3
…
y
…
m
n
0
…
(1)、该函数图象的对称轴是______;(2)、该函数图象与轴的交点的坐标是______;(3)、当时,的取值范围是______;(4)、不等式的解集是______. -
8、如图,在中, , , , 点从点开始沿边运动,速度为 . 与此同时,点从点开始沿边运动,速度为 . 当点到达点时,点同时停止运动.连接 , 设运动时间为 , 的面积为 .
 (1)、用含的代数式表示:______cm,______cm;(2)、当为何值时?
(1)、用含的代数式表示:______cm,______cm;(2)、当为何值时? -
9、解方程:
-
10、如图,已知 , 均为等腰直角三角形, , 为的中点,的延长线交线段于点 , 连接 . 若 , , 则 .

-
11、已知抛物线(为常数,)经过点 , , 且 , 则下列四个结论:①;②;③若方程有两个不相等的实数根(且),则;④若 , 抛物线过点 , 且 , 则 . 其中正确的结论是(填序号).
-
12、若关于的方程的两个实数根互为相反数,则的值是 .
-
13、某航空公司有若干个飞机场,每两个飞机场之间都开辟了一条航线,一共开辟了条航线,这个航空公司共有个飞机场.
-
14、在平面直角坐标系中,将函数的图象记为 , 将绕原点旋转得到图象 , 把和合起来的图形记为图形 . 则当时,直线与图形的交点的个数是( )A、2 B、4 C、2或3 D、3或4
-
15、如图,四边形内接于 , , , 的直径为 , 四边形的周长为 , 的长为 , 则关于的函数关系式是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、已知抛物线上有三个点 , , , 若 , , , 则 , , 的大小关系是( )A、 B、 C、 D、
-
17、在平面直角坐标系中,点坐标 , 以为圆心,4个单位长度为半径作圆,下列正确的是( )A、原点在内 B、原点在上 C、与轴相切,与轴相交 D、与轴相切,与轴相交
-
18、如图,将绕点逆时针旋转,点的对应点为 , 点的对应点为 , 若恰好是线段与的交点,且 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、如图,内接于 , 连 , 若 , 则的度数是( )
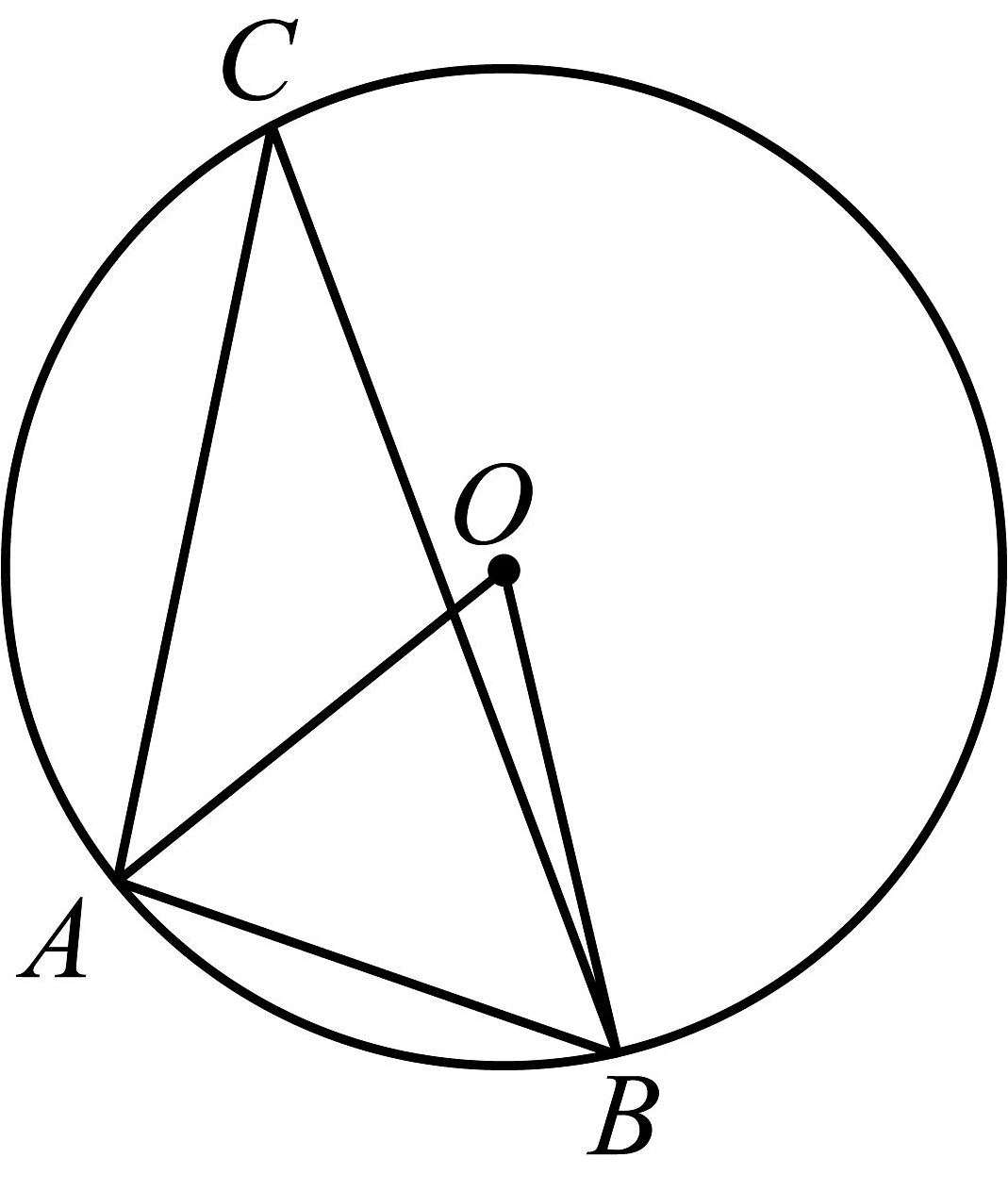 A、 B、 C、 D、
A、 B、 C、 D、 -
20、关于抛物线 , 下列说法正确的是( )A、开口向上 B、对称轴是直线 C、函数有最小值 D、可由抛物线向右平移个单位再向下平移个单位而得