相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、(1)、请从①、②两个小题中任选一个作答.
①解方程:;
②解不等式组: .
(2)、先化简,再求值: , 其中x的值是(1)中的正整数解. -
2、如图,已知 , 以点O为圆心,2为半径画弧,交于点M,交于点N,分别以点M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点C,画射线交于点E,连接 .
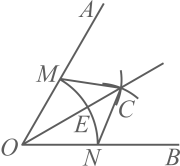 (1)、求证:;(2)、若 , 求的长.
(1)、求证:;(2)、若 , 求的长. -
3、计算: .
-
4、四边形中,与交于点O,O是的中点, , 已知 , , , 则的长为 .

-
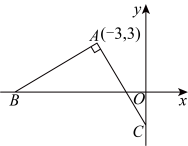
5、如图,在平面直角坐标系中,已知点 , 点B是x轴负半轴上的动点,点C是y轴负半轴上的动点, , 则 .
-
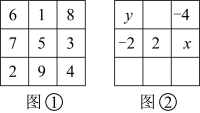
6、幻方的历史悠久,传说最早出现在夏禹时代的“洛书”中.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图①),将9个数填在(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图②的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则 .
-
7、若关于x的一元二次方程有两个相等的实数根,则 .
-
8、2025年5月29日1时31分,西昌卫星发射中心用长征三号乙运载火箭发射天问二号探测器取得圆满成功.此次发射任务,火箭的入轨速度要达到千米/秒,用科学记数法表示这个速度为米/秒.
-
9、已知抛物线(a,b,c是常数且)的自变量x与函数y的部分对应值如下表:
x
…
0
1
2
3
4
…
y
…
m
n
s
…
其中 . 以下结论:①;②若抛物线经过点则;③关于x的方程有两个不相等的实数根;④;⑤当时,y的最小值是1,则或4.其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个 -
10、如图①,有一水平放置的正方形 , 点D为的中点,等腰满足顶点A,B在同一水平线上且 , 点B与的中点重合.等腰以每秒1个单位长度的速度水平向右匀速运动,当点B运动到点D时停止.在这个运动过程中,等腰与正方形重叠部分的面积y与运动时间t(s)之间的对应关系如图②所示,下列说法错误的是( )
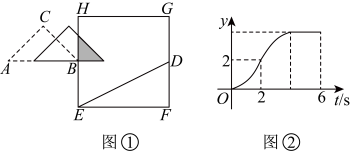 A、 B、 C、当时, D、的周长为
A、 B、 C、当时, D、的周长为 -
11、如图,是的弦,过圆心O作于点H,交于点A, , 点M是上异于C,D的一点,连接 , , 则的值是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、如图,在正八边形中,对角线 , 交于点K,则=( )
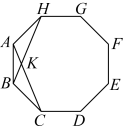 A、 B、 C、 D、
A、 B、 C、 D、 -
13、如图,在平行四边形中, , 对角线 , 交于点O,点P是的中点,连接 , 点E是的中点,连接 , 则的长是( )
 A、1 B、 C、2 D、4
A、1 B、 C、2 D、4 -
14、如图,在长为 , 宽为的矩形地面的四周种植花卉,中间种植草坪.如果要求花卉带的宽度相同,且草坪的面积为总面积的 , 那么花卉带的宽度应为多少米?设花卉带的宽度为 , 则可列方程为( )
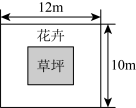 A、 B、 C、 D、
A、 B、 C、 D、 -
15、为用好红色资源,讲好红色故事,李老师安排了10名学生收集红色文化书籍,他们收集到的红色文化书籍本数如下表:
书籍本数
2
3
4
5
6
人数
2
2
2
3
1
下列关于书籍本数的描述正确的是( )
A、众数是3 B、平均数是3 C、中位数是4 D、方差是1 -
16、下列运算正确的是( )A、 B、 C、 D、
-
17、下列几何体中,其三视图的主视图和左视图不相同的是( )A、
 B、
B、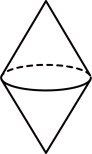 C、
C、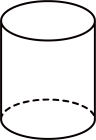 D、
D、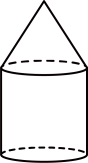
-
18、的相反数是( )A、 B、 C、2 D、4
-
19、如图,在中,平分 , , 于点E,点F在上, .
 (1)、求证: .(2)、若 , , 求的长.
(1)、求证: .(2)、若 , , 求的长. -
20、计算:(1)、;(2)、;