相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
1、某校计划开设五项活动:跳绳、篮球、乒乓球、跑步、踢毽子.为了解学生对这五项活动的喜爱情况,在全校随机抽取部分学生进行问卷调查(每个被调查的学生必须选择且只能选择其中一项),统计整理并绘制了如下两幅不完整的统计图:根据统计图提供的信息,解答下列问题:
 (1)、本次问卷调查的学生共有________人,并补全条形统计图;“乒乓球”所对应的扇形圆心角的度数为________度;(2)、学校体育老师从喜欢篮球项目的甲、乙、丙、丁四名同学中任选两名进行个别访谈,请用列表法或画树状图法求抽取的两人恰好是甲和乙的概率.
(1)、本次问卷调查的学生共有________人,并补全条形统计图;“乒乓球”所对应的扇形圆心角的度数为________度;(2)、学校体育老师从喜欢篮球项目的甲、乙、丙、丁四名同学中任选两名进行个别访谈,请用列表法或画树状图法求抽取的两人恰好是甲和乙的概率. -
2、解方程组:
-
3、如图,菱形的边长为 , , 点为菱形内一动点,连接 , , 点为的中点,连接 , 则的最小值为 .

-
4、如图,一束平行于主光轴的光线经凹透镜折射后,其折射光线所在的直线与一束经过光心O的光线相交于点P,F为凹透镜的焦点.若 , , 则的度数为 .

-
5、不等式的解集为 .
-
6、如图,是的内接正n边形的一边,点C在上, , 则n的值是( )
 A、8 B、9 C、10 D、11
A、8 B、9 C、10 D、11 -
7、如图,菱形的顶点 , 在x轴上,点C在y轴正半轴上,那么菱形的面积( )
 A、16 B、 C、12 D、
A、16 B、 C、12 D、 -
8、已知二次函数 , 当时,的取值范围是( )A、 B、 C、 D、
-
9、已知一组数据33,42,42,4●,51,68,第四个两位数的个位数字被墨水涂污,关于这组数据,下列统计量的计算结果与被涂污数字无关的是( )A、平均数 B、方差 C、中位数 D、众数
-
10、下列四幅节气作品分别代表“立春”“谷雨”“白露”“大雪”,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
11、如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
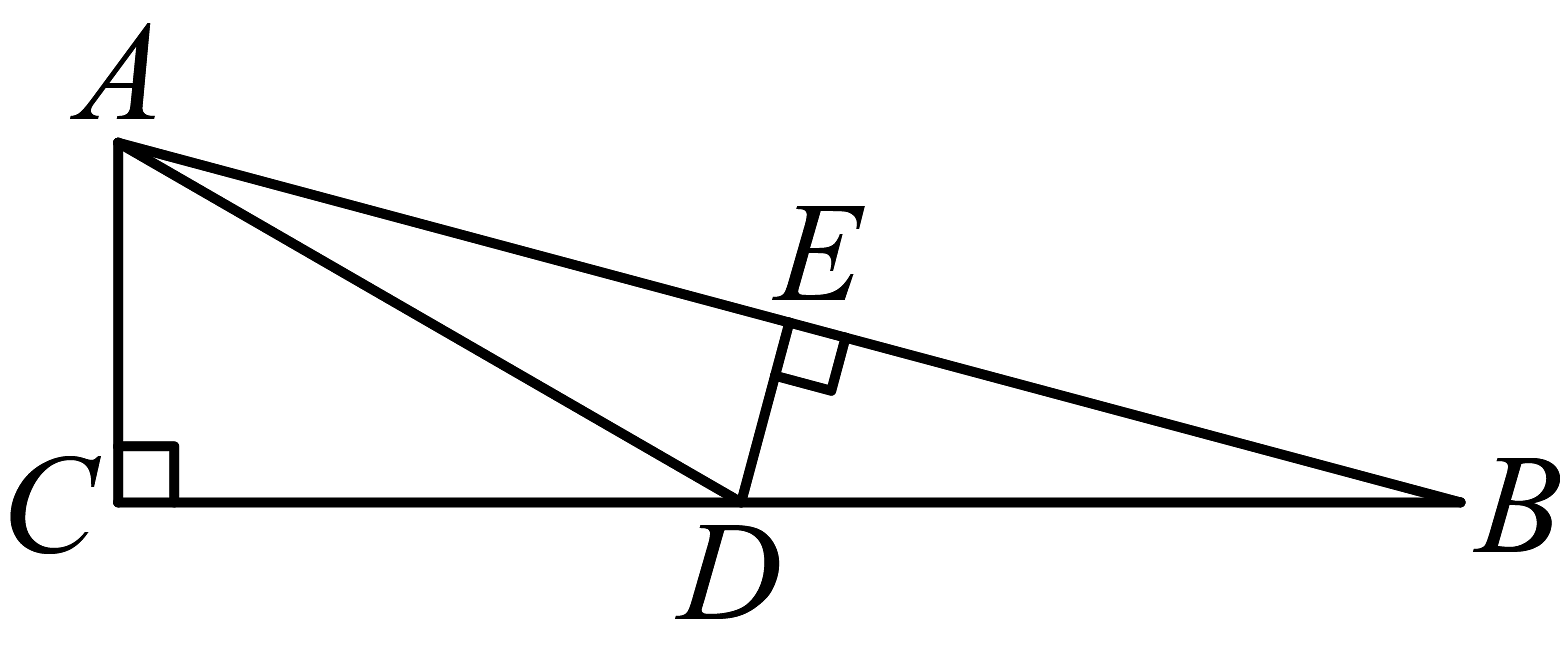
12、如图所示, , , , , , 则

-
13、如图,已知抛物线的顶点为 , 且经过点 .
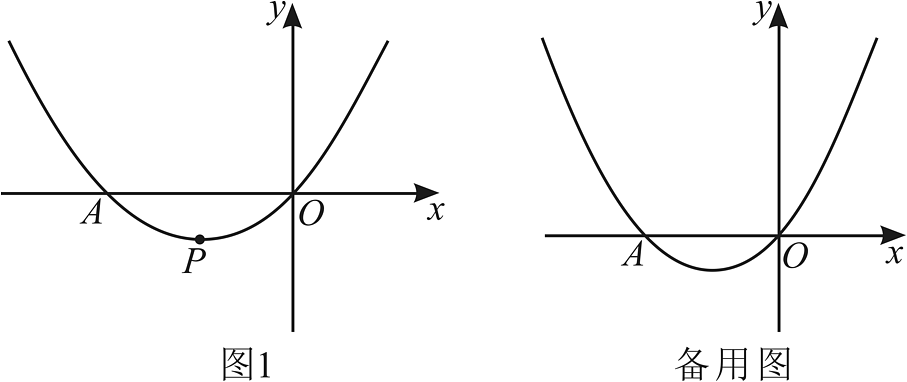 (1)、求抛物线的函数表达式;(2)、过点的一条直线与抛物线交于点 , 且满足 , 求点的坐标;(3)、过点作轴的平行线交轴于点 , 过点的直线与抛物线交于 , 两点,求的值.
(1)、求抛物线的函数表达式;(2)、过点的一条直线与抛物线交于点 , 且满足 , 求点的坐标;(3)、过点作轴的平行线交轴于点 , 过点的直线与抛物线交于 , 两点,求的值. -
14、根据以下素材,探索完成任务.
素材1
某广场的音乐喷泉形状如抛物线(图1),其出水口不变,抛物线的形状随音乐的节奏起伏变化而变化,出水口离岸边18米(图2).

素材2
设其出水口为原点,音乐变化时,抛物线的顶点在直线上变动,从而产生一组不同的抛物线(图3),这组抛物线的统一形式为 . 例如当时,直线 , 若抛物线最大高度达2米,则此时抛物线的顶点坐标为 .
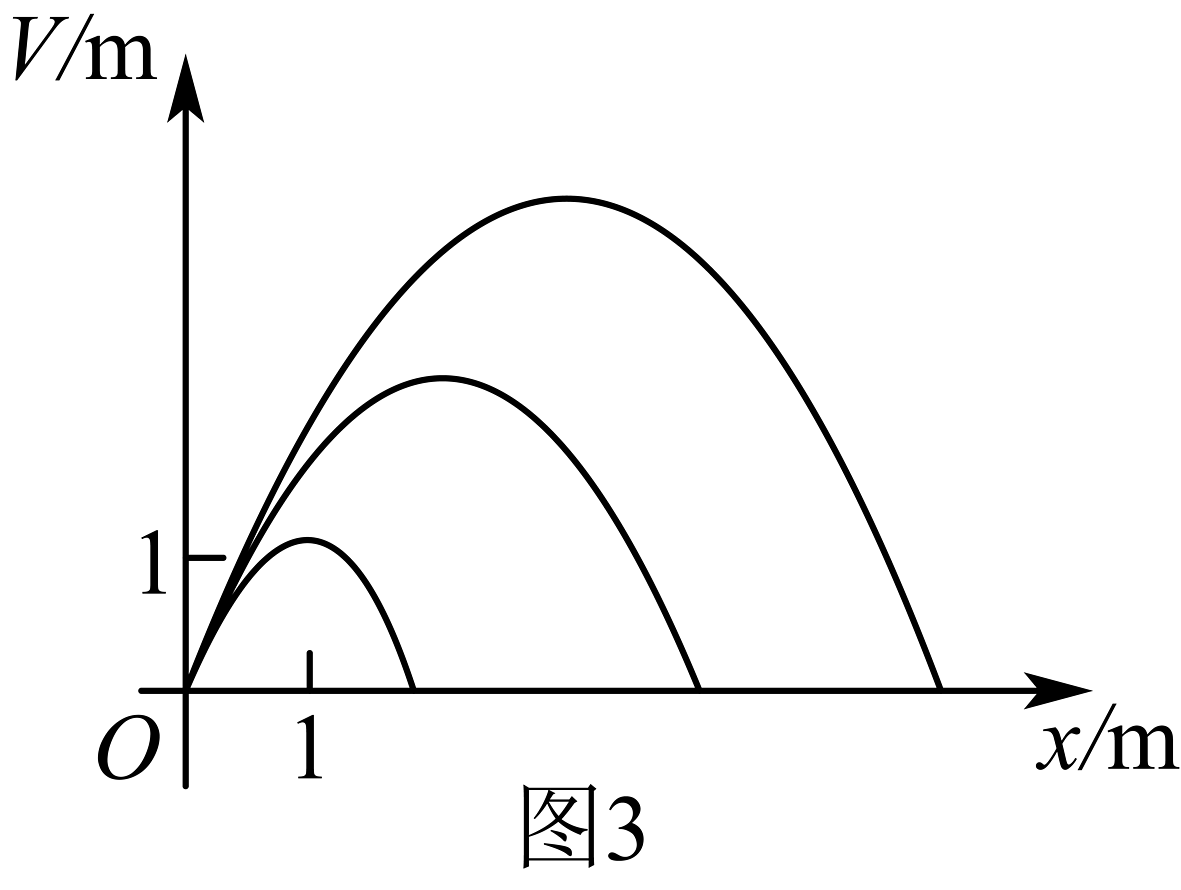
素材3
若是函数图象上一点,则 , 得 .
任务一
若已知 , 且喷出的抛物线水线最大高度达3米,求此时抛物线的顶点坐标及a、b的值.
任务二
若 , 喷出的水恰好达到岸边,求此时喷出的抛物线水线最大高度.
任务三
若 , 要使喷出的抛物线水落地时离岸边不能少于米且不能超出2米,求k的范围.
-
15、在“全民阅读月”活动中,某校提供了四类适合学生阅读的书籍:A文学类,B科幻类,C漫画类,D数理类.为了解学生阅读兴趣,学校随机抽取了部分学生进行调查(每位学生仅选一类).根据收集到的数据,整理后得到下列不完整的图表:
书籍类别
学生人数
A文学类
24
B科幻类
C漫画类
16
D数理类
8
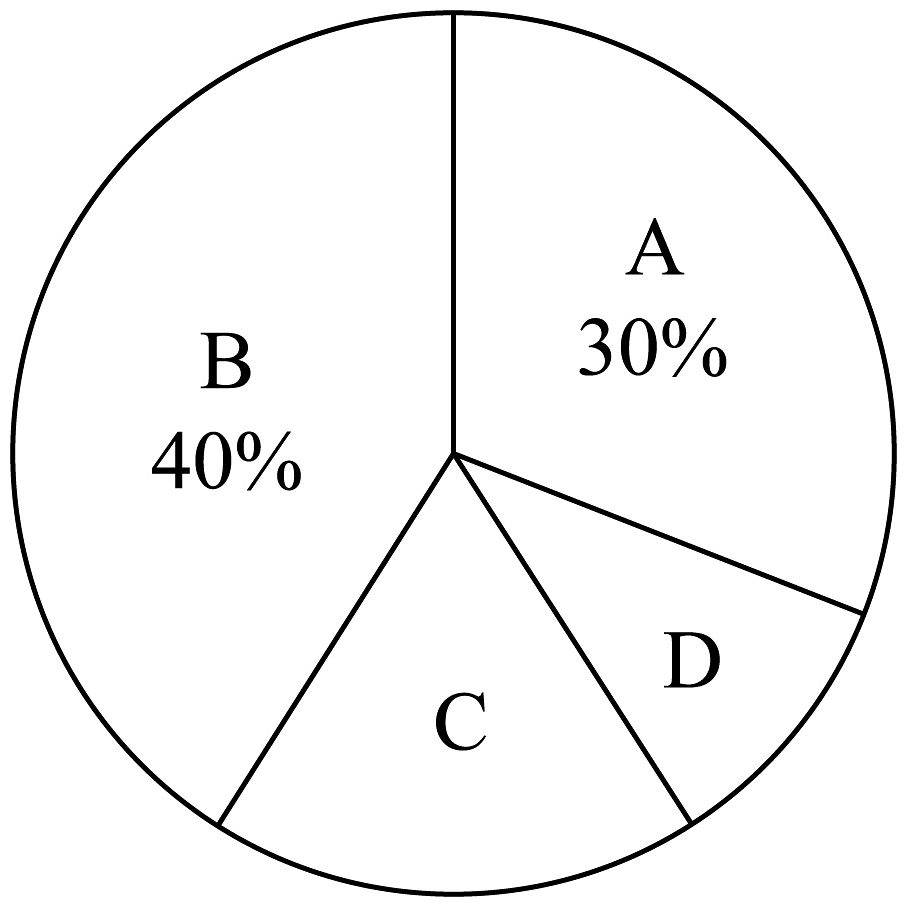 (1)、本次抽查的学生人数是______,统计表中的______.(2)、若该校共有1200名学生,请你估计该校学生选择“D”数理类”书籍的学生人数;(3)、学校决定成立“文学”“科幻”“漫画”“数理”四个阅读社团.若小文、小明随机选取四个社团中的一个,请利用列表或画树状图的方法,求他们选择同一社团的概率.
(1)、本次抽查的学生人数是______,统计表中的______.(2)、若该校共有1200名学生,请你估计该校学生选择“D”数理类”书籍的学生人数;(3)、学校决定成立“文学”“科幻”“漫画”“数理”四个阅读社团.若小文、小明随机选取四个社团中的一个,请利用列表或画树状图的方法,求他们选择同一社团的概率. -
16、(1)化简:;
(2)若是方程的根,求的值.
-
17、如图,在中,点 , 分别是对角线上的两点,且 , 连结 , . 求证: .
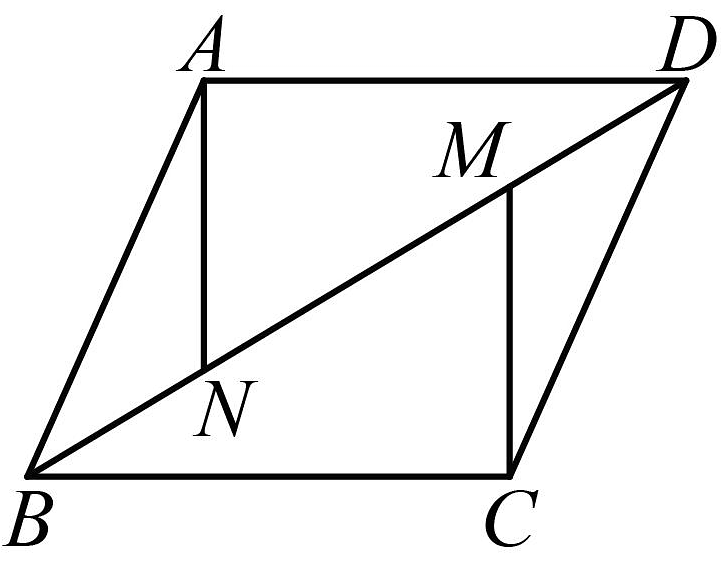
-
18、解方程组: .
-
19、如图,是线段上一点,和是位于直线同侧的两个等边三角形,点分别是的中点.若 , 则下列结论正确的有 . (填序号)
①的最小值为;②的最小值为;③周长的最小值为6;④四边形面积的最小值为 .
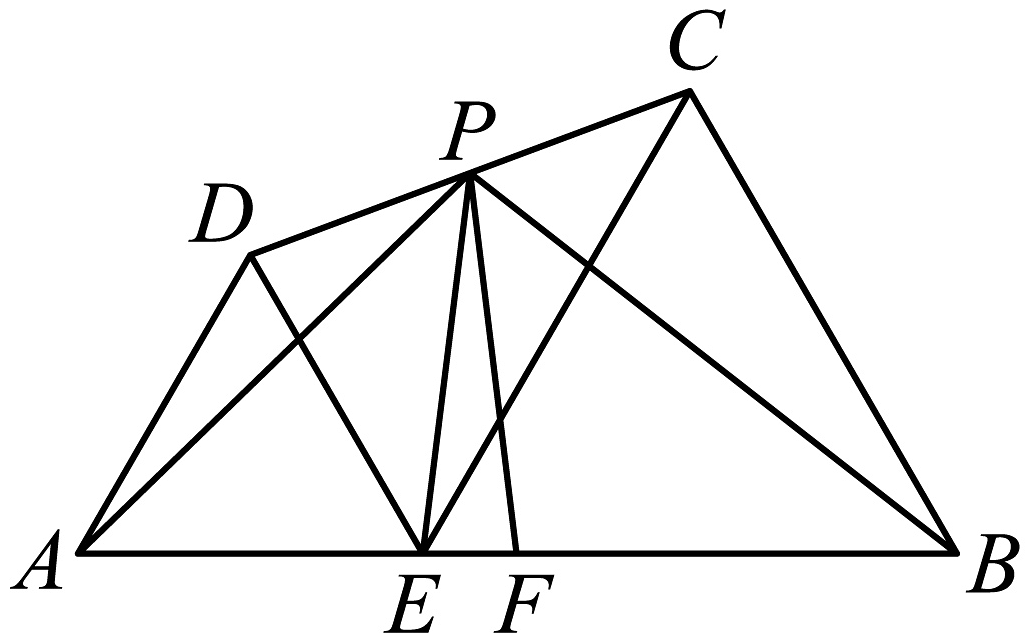
-
20、如图,在中, , , 的垂直平分线交于 , 交于 , 若 , 则的长为 .