相关试卷

1、2025蛇年春晚以“巳巳如意，生生不息”为主题，寓意着事事如意、生生不息的美好祝愿．下图为春晚主标识，通过双“巳”对称摆放形成如意的纹样，它采用的数学变换是（）

A、平移 B、旋转 C、轴对称 D、位似

查看解析
2、下列各数，是负整数的是（）

A、0 B、 $- π$ C、1 D、 $- 2$

查看解析
3、如图，矩形 $O A B C$ 的顶点 $A$ 、 $C$ 分别在 $x$ 、 $y$ 轴的正半轴上，点 $D$ 为对角线 $O B$ 的中点，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限内的图象经过点 $D$ ，与 $A B$ 相交于点 $E$ ，且点 $B (4, 2)$ ．

(1)、求反比例函数 $y = \frac{k}{x}$ 的关系式；

(2)、求 $△ O D E$ 的面积；

(3)、若反比例函数的图象与矩形的边 $B C$ 交于点 $F$ ，将矩形折叠，使点 $O$ 与点 $F$ 重合，折痕分别与 $x$ 、 $y$ 轴正半轴交于点 $H$ 、 $G$ ，求直线 $G H$ 的函数关系式．

查看解析
4、2024年6月6日是第29个全国“爱眼日”，主题是关注普遍的眼健康．为科学防控近视，关注孩子眼睛的健康．希望学校在“爱眼日”当天随机抽取50名学生进行视力检测，并将结果分成A（ $4.0 \leq x < 4.2$ ），B（ $4.2 \leq x < 4.4$ ），C（ $4.4 \leq x < 4.6$ ），D（ $4.6 \leq x < 4.8$ ），E（ $4.8 \leq x < 5.0$ ），F（ $5.0 \leq x$ ）六组，进行数据整理，已知视力标准的正常值 $\geq 5.0$ ，信息如下：
A．视力频数分布表：
视力（x）
A（ $4.0 \leq x < 4.2$ ）
B（ $4.2 \leq x < 4.4$ ）
C（ $4.4 \leq x < 4.6$ ）
D（ $4.6 \leq x < 4.8$ ）
E（ $4.8 \leq x < 5.0$ ）
F（ $5.0 \leq x$ ）
频数
5
8
9
m
7
n
B．D组的数据分别为：
4.6，4.6，4.7，4.7，4.7，4.7，4.7，4.6，4.7，4.6，4.6，4.7，4.7，4.6
请根据以上信息，回答下列问题：

(1)、 $m =$ ______， $n =$ ______；

(2)、本次调查视力情况的中位数为______，视力正常的人数占被调查人数的百分比为______；

(3)、请对该校学生的视力情况作出评价，并提出两条合理化建议．

查看解析
5、如图， $⊙ O$ 是 $△ A B C$ 的外接圆，直径 $A B = 4 cm, ∠ A = 25 °$ ．

(1)、以点C为顶点，BC为边，在 $B C$ 的右侧作 $∠ B C P = ∠ A$ ，交 $A B$ 的延长线于点P：（要求：尺规作图，不写作法，保留作图痕迹）

(2)、在（1）所作的图中，求证： $C P$ 是 $⊙ O$ 的切线．

查看解析
6、如图，等腰 $Rt △ A B C$ 中 $∠ A C B = 90 °, A B = 4$ ，点P为斜边中点，点D在 $C B$ 上且 $C D = 1$ ，将 $C D$ 绕点C在平面内旋转，点D的对应点为点Q，连接 $P Q$ ．则 $P Q$ 的最大值为．

查看解析
7、在平面直角坐标系中，点 $P (2, - 6)$ 关于y轴对称的点的坐标是．

查看解析
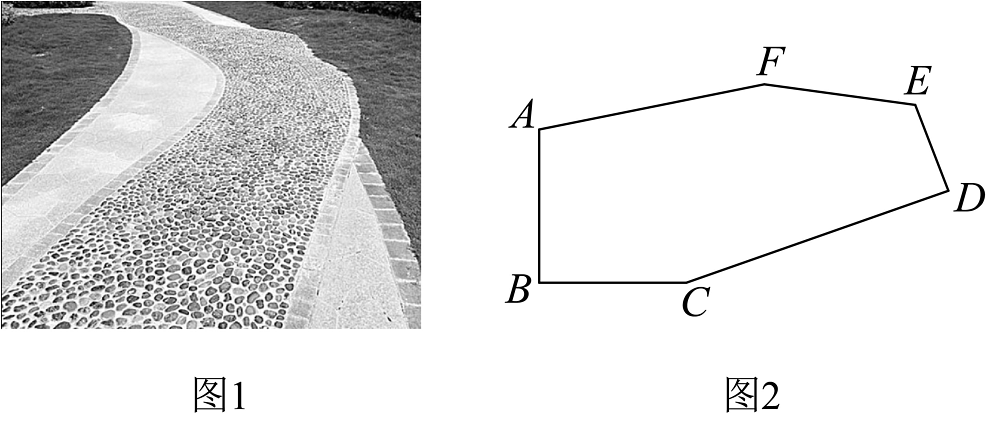
8、如图1，小亮在公园发现一条由一些不规则的多边形拼接而成的道路．小亮由此抽象出如图2所示的多边形 $A B C D E F$ ，则这个多边形的内角和为．

查看解析
9、如图，先以正方形 $A B C D$ 的边 $A D$ 为直径画圆，然后以 $A$ 为圆心， $A B$ 为半径画 $\overset{⌢}{B D}$ ，最后以 $A B$ 的中点 $E$ 为圆心， $B E$ 为半径画 $\overset{⌢}{B F}$ 与 $\overset{⌢}{A D}$ 交于点 $F$ ，若 $A D = 2$ ，则图中阴影部分的面积为（）

A、 $\frac{3}{2} π - 1$ B、 $π - 1$ C、4 D、 $π + 1$

查看解析
10、圆在中式建筑中有着广泛的应用，如图，某园林中圆弧形门洞的顶端到地面的高度为 $2.8m$ ，地面入口的宽度为 $1m$ ，门枕的高度为 $0.3m$ ，则该圆弧所在圆的半径为（）

A、 $1.2m$ B、 $1.3m$ C、 $1.4m$ D、 $0.5m$

查看解析
11、在函数 $y = - 2 x^{2} - 4 x + a$ （a为常数）的图象上有三点 $(- 2, y_{1}), (- 1, y_{2}), (1, y_{3})$ ，则函数值 $y_{1}, y_{2}, y_{3}$ 的大小关系为（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看解析
12、一般情况下，酚酞在酸性和中性溶液中保持无色，而在碱性溶液中则会呈现红色，在一次化学实验课上，学生们使用酚酞试液来检测四瓶标签模糊、无法辨认的无色溶液的酸碱性．已知这四瓶溶液分别是：
小明随机选取一瓶溶液并滴入酚酞试液，这瓶溶液变红的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看解析
13、 $D e e p S e e k$ （深度求索）是由中国某AI公司开发的通用人工智能系统．截至 $2025$ 年 $3$ 月， $D e e p S e e k$ 的全球日活跃用户总量达到 $1.94$ 亿，将数据 $1.94$ 亿用科学记数法表示是（）

A、 $19.4 \times 10^{7}$ B、 $0.194 \times 10^{9}$ C、 $1.94 \times 10^{9}$ D、 $1.94 \times 10^{8}$

查看解析
14、第十五届全国运动会将于2025年11月9日至21日在粤港澳大湾区举办，惠州作为赛事承办城市之一，将举办跆拳道、滑板、轮滑等赛事，下列给出的运动图片是轴对称图形的是（）

A、 B、 C、 D、

查看解析
15、如图1，在 $△ A B C$ 中， $A B = A C = 15$ ， $B C = 24$ ，点 $P$ 以每秒1个单位长度的速度，从点 $A$ 出发沿 $A B$ 方向向终点 $B$ 运动，同时，点 $Q$ 以每秒2个单位长度的速度，从点 $B$ 出发沿 $B C$ 方向向终点 $C$ 运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为 $t$ 秒，请解答下列问题：

(1)、当 $t$ 为何值时， $P Q ∥ A C$ ；

(2)、在点 $P$ 、 $Q$ 的运动过程中，是否存在某一时刻 $t$ ，使得 $△ P C Q$ 的面积等于6？若存在，请求出 $t$ 的值；若不存在，请说明理由．

(3)、如图2， $E$ 是 $A C$ 的中点，连接 $B E$ ，与 $P Q$ 交于点 $O$ ，是否存在某一时刻 $t$ ，使得 $P Q ⊥ B E$ ？若存在，请求出 $t$ 的值；若不存在，请说明理由．

查看解析
16、在 $△ A B C$ 中， $A B = A C$ ，点D是 $B C$ 边上一点（不与端点重合），连接 $A D$ ．将线段 $A D$ 绕点A逆时针旋转 $α$ 得到线段 $A E$ ，连接 $D E$ ．

(1)、如图1， $α = ∠ B A C = 60 °$ ， $∠ C A E = 20 °$ ，求 $∠ A D B$ 的度数；

(2)、如图2， $α = ∠ B A C = 90 °$ ， $B D < C D$ ，过点 $D$ 作 $D G ⊥ B C$ ， $D G$ 交 $C A$ 的延长线于 $G$ ，连接 $B G$ ．点 $F$ 是 $D E$ 的中点，点 $H$ 是 $B G$ 的中点，连接 $F H$ ， $C F$ ．用等式表示线段 $F H$ 与 $C F$ 的数量关系并证明：

(3)、如图3， $∠ B A C = 120 °$ ， $α = 60 °$ ， $A B = 8$ ，连接 $B E$ ， $C E$ ．点 $D$ 从点 $B$ 移动到点 $C$ 过程中，将 $B E$ 绕点 $B$ 逆时针旋转 $60 °$ 得线段 $B M$ ，连接 $E M$ ，作 $M N ⊥ C A$ 交 $C A$ 的延长线于点 $N$ ．当 $C E$ 取最小值时，在直线 $A B$ 上取一点 $P$ ，连接 $P E$ ，将 $△ A P E$ 沿 $P E$ 所在直线翻折到 $△ A B C$ 所在的平面内，得 $△ Q P E$ ，连接 $B Q$ ， $M Q$ ， $N Q$ ，当 $B Q$ 取最大值时，请直接写出 $△ M N Q$ 的面积．

查看解析
17、如图，在平面直角坐标系中，抛物线 $y = x^{2} + b x + c$ 与x轴交于A， $B (6, 0)$ 两点，与 $y$ 轴交于点 $C$ ，抛物线的对称轴是直线 $x = \frac{5}{2}$ ．

(1)、求抛物线的表达式：

(2)、点P是射线 $B C$ 下方抛物线上的一动点，连接 $O P$ 与射线 $B C$ 交于点Q，点D，E为抛物线对称轴上的动点（点E在点D的下方），且 $D E = 4$ ，连接 $B D$ ， $P E$ ．当 $\frac{P Q}{O Q}$ 取得最大值时，求点P的坐标及 $B D + P E$ 的最小值；

(3)、在（2）中 $\frac{P Q}{O Q}$ 取得最大值的条件下，将抛物线 $y = x^{2} + b x + c$ 沿射线 $B C$ 方向平移 $2 \sqrt{2}$ 个单位长度得到抛物线 $y^{'}$ ，点M为点P的对应点，点N为抛物线 $y^{'}$ 上的一动点．若 $∠ N A B = ∠ O P M - 45 °$ ，请直接写出所有符合条件的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．

查看解析
18、为加强森林防火，某林场采用人工瞭望与无人机巡视两种方式监测森林情况．如图，A，B，C，D在同一平面内．A是瞭望台，某一时刻，观测到甲无人机位于A的正东方向10千米的B处，乙无人机位于A的南偏西 $30 °$ 方向20千米的D处．两无人机同时飞往C处巡视，D位于C的正西方向上，B位于C的北偏西 $30 °$ 方向上．（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ， $\sqrt{5} \approx 2.24$ ， $\sqrt{7} \approx 2.65$ ）

(1)、求 $B D$ 的长度（结果保留小数点后一位）；

(2)、甲、乙两无人机同时分别从B，D出发沿 $B C ， D C$ 往C处进行巡视，乙无人机速度为甲无人机速度的2倍．当两无人机相距20千米时，它们可以开始相互接收到信号．请问甲无人机飞离B处多少千米时，两无人机可以开始相互接收到信号（结果保留小数点后一位）？

查看解析
19、如图，点 $O$ 为矩形 $A B C D$ 的对角线AC的中点， $A B = 3$ ， $B C = 4$ ， $E$ ， $F$ 是 $A C$ 上的点（ $E$ ， $F$ 均不与 $A$ ， $C$ 重合），且 $A E = C F$ ，连接 $B E$ ， $D F$ ．用 $x$ 表示线段 $A E$ 的长度，点 $E$ 与点 $F$ 的距离为 $y_{1}$ ．矩形 $A B C D$ 的面积为 $S$ ， $△ A B E$ 的面积为 $S_{1}$ ， $△ C D F$ 的面积为 $S_{2}$ ， $y_{2} = \frac{S}{S_{1} + S_{2}}$ ．

(1)、请直接写出 $y_{1}$ ， $y_{2}$ 分别关于 $x$ 的函数表达式，并写出自变量 $x$ 的取值范围：

(2)、在给定的平面直角坐标系中画出函数 $y_{1}$ ， $y_{2}$ 的图象，并分别写出函数 $y_{1}$ ， $y_{2}$ 的一条性质；

(3)、结合函数图象，请直接写出 $y_{1} < y_{2}$ 时 $x$ 的取值范围（近似值保留小数点后一位，误差不超过 $0.2$ ）．

查看解析
20、列方程解下列问题：
某厂生产甲、乙两种文创产品．每天生产甲种文创产品的数量比每天生产乙种文创产品的数量多50个，3天时间生产的甲种文创产品的数量比4天时间生产的乙种文创产品的数量多100个．

(1)、求该厂每天生产的甲、乙文创产品数量分别是多少个？

(2)、由于市场需求量增加，该厂对生产流程进行了改进．改进后，每天生产乙种文创产品的数量较改进前每天生产的数量增加同样的数量，且每天生产甲种文创产品的数量较改进前每天增加的数量是乙种文创产品每天增加数量的2倍．若生产甲、乙两种文创产品各1400个，乙比甲多用10天，求每天生产的乙种文创产品增加的数量．

查看解析

上一页 793 794 795 796 797 下一页跳转

视力（x）	A（ $4.0 \leq x < 4.2$ ）	B（ $4.2 \leq x < 4.4$ ）	C（ $4.4 \leq x < 4.6$ ）	D（ $4.6 \leq x < 4.8$ ）	E（ $4.8 \leq x < 5.0$ ）	F（ $5.0 \leq x$ ）
频数	5	8	9	m	7	n