相关试卷

1、如图，扇形 $A O B$ 的圆心角为 $60^{\circ}$ 点 $C$ 是 $O A$ 的中点，连接 $C B$ ．若 $O A = 4$ ，则图中阴影部分的面积为（　　）

A、 $\frac{4 π}{3} - \sqrt{3}$ B、 $\frac{8 π}{3} - \sqrt{3}$ C、 $\frac{4 π}{3} - 2 \sqrt{3}$ D、 $\frac{8 π}{3} - 2 \sqrt{3}$

查看解析
2、实数m对应的点在数轴上的位置如图所示，则不等式组 $\{\begin{array}{l} x + 2 > 0 \\ x - m \leq 0 \end{array}$ 的解集为（）

A、 $x > - 2$ B、 $x \leq m$ C、 $- 2 < x \leq m$ D、 $- 2 < x < m$

查看解析
3、国产大模型DeepSeek已经成为全球增长最快的AI工具，其每月新增网站访问量已超过OpenAI的ChatGPT．据报道，2025年2月，DeepSeek访问量达到525000000次，将数字525000000用科学记数法表示为（）

A、 $5.25 \times 10^{6}$ B、 $5.25 \times 10^{8}$ C、 $5.25 \times 10^{- 6}$ D、 $5.25 \times 10^{- 8}$

查看解析
4、下列实数的绝对值最大的是（）

A、 $- 10$ B、 $4 \sqrt{5}$ C、 $- 2^{3}$ D、 ${(- 3)}^{2}$

查看解析
5、已知：抛物线 $y = \frac{1}{4} a x^{2} + a$ 的顶点落在直线l： $y = x + 1$ 上，

(1)、求该抛物线的解析式；

(2)、将l向上平移b（b>0）个单位，设其与抛物线的交点分别为 $N_{1}$ ， $N_{2}$ ，（ $N_{1}$ 在 $N_{2}$ 左侧）
①请用b表示 $S_{△ N_{1} O N_{2}}$ ；
②当 $b = 1$ 时，设此时l与y轴交点为F，将l绕点F转动，转动后与抛物线的交点设为 $M_{1}$ ， $M_{2}$ （ $M_{1}$ 在 $M_{2}$ 左侧），过 $M_{1}$ ， $M_{2}$ 分别作x轴的垂线，垂足分别为点 $P_{1}$ ， $P_{2}$ ，连接 $P_{1} M_{2}$ ， $P_{2} M_{1}$ ，设其交点为T，求转动过程中，T到直线 $M_{1} M_{2}$ 距离的最大值．

查看解析
6、如图，在正方形ABCD中，AB＝4，动点P从点A出发，以每秒2个单位的速度，沿线段AB方向匀速运动，到达点B停止．连接DP交AC于点E，以DP为直径作⊙O交AC于点F，连接DF、PF．
（1）求证：△DPF为等腰直角三角形；
（2）若点P的运动时间t秒．
①当t为何值时，点E恰好为AC的一个三等分点；
②将△EFP沿PF翻折，得到△QFP，当点Q恰好落在BC上时，求t的值．

查看解析
7、如图，平行四边形 $O A B C$ 的顶点O与原点重合， $A O$ 边在x轴的正半轴上，且点 $C (3, 4)$ ， $A (3, 0)$ ，反比例函数 $y = \frac{k}{x} (k > 0, x > 0)$ 的图象经过对角线 $O B$ 的中点D．

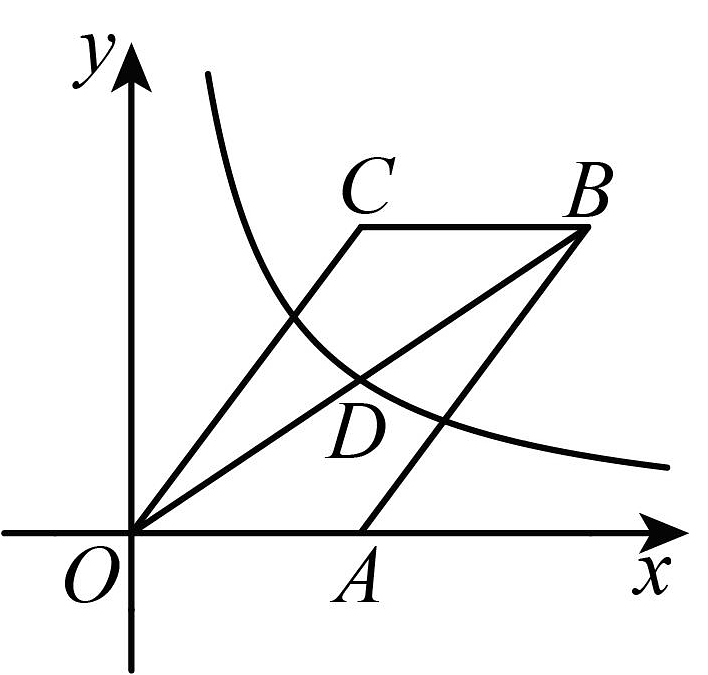(1)、求反比例函数的表达式．

(2)、已知线段 $O D$ 的垂直平分线分别交 $O D$ ， $O A$ 于点M，N．求 $A N$ 的值．

查看解析
8、今年夏天，多地连降大雨，某地因大雨导致山体塌方，致使车辆通行受阻，某工程队紧急抢修，需要爆破作业．现有A，B两种导火索，A种导火索的燃烧速度是B种导火索燃烧速度的 $\frac{2}{3}$ ，同样燃烧长度为36cm的导火索，A种所需时间比B种多 $20 s$ ．
（1）求A，B两种导火索的燃烧速度分别是多少？
（2）为了安全考虑，工人选燃烧速度慢的导火索进行爆破，一工人点燃导火索后以6m/s的速度跑到距爆破点100m外的安全区，问至少需要该种导火索多长？

查看解析
9、已知 $A = (1 - \frac{5}{x + 4}) \div \frac{x^{2} - 2 x + 1}{x + 4}$ ．

(1)、化简A；

(2)、已知x满足 $x^{2} + x - 12 = 0$ ，求A的值．

查看解析
10、疫情就是命令，防控就是责任.为了解学生对疫情防控知识的了解情况，某校学生会随机抽取了部分学生进行疫情防控知识线上问卷调查，将他们的得分从高到低依次按优秀、良好、合格、待合格（分别记为 $A$ ， $B$ ， $C$ ， $D$ ）四个等级进行统计，并绘制了如下不完整的两幅统计图．
请根据以上信息，解答下列问题：

(1)、本次线上问卷，共调查了______名学生，扇形统计图中， $B$ 部分的圆心角是______度；

(2)、补全条形统计图；

(3)、若该校有2000名学生，估计疫情防控知识问卷调查得分能达到良好及以上的人数．

查看解析
11、解方程组： $\{\begin{matrix} 5 x + y = 6 \\ 2 x - y = 8 \end{matrix}$ ．

查看解析
12、在练习掷铅球项目时，某同学掷出的铅球在操场地上砸出一个直径为 $6 cm$ 、深 $2 cm$ 的小坑，则该铅球的直径为 $cm$ ．

查看解析
13、从2，3，3，4中随机抽取两个数，抽到两个都是这组数据的众数的概率．

查看解析
14、二次函数 $y = a x^{2} + b x + c$ 的图像如图所示，则一次函数 $y = a b x + c$ 的图像大致是（）

A、 B、 C、 D、

查看解析
15、如图是一个不倒翁的主视图，不倒翁的圆形脸恰好与帽子边沿 $P A$ ， $P B$ 分别相切于点 $A, B$ ，不倒翁的鼻尖正好是圆心O，若 $∠ O A B = 25 °$ ，则 $∠ A P B$ 的度数为（）．

A、 $50 °$ B、 $60 °$ C、 $25 °$ D、 $90 °$

查看解析
16、下列运算正确的是（）

A、 $\sqrt{25} = \pm 5$ B、 $\sqrt{0.4} = 0.2$ C、 ${(- 1)}^{- 1} = - 1$ D、 ${(- 3 m n)}^{2} = - 6 m^{2} n^{2}$

查看解析
17、如图，直线 $A B$ 、 $C D$ 分别与 $E F$ 、 $G H$ 相交，已知 $∠ 1 = 100 °$ ， $∠ 2 = 115 °$ ， $∠ 3 = 65 °$ ，那么 $∠ 4 =$ ．

查看解析
18、乒乓球是一项集力量、速度、灵敏度、协调性和判断力于一体的综合性运动，在2024年巴黎奥运会乒乓球比赛中，中国队包揽了全部5块金牌．运动员常使用乒乓球发球机进行日常训练，如图所示， $O$ 点在球台中轴线上，发球机的出球 $O A$ 在 $O$ 点正上方 $0.3 m$ 处，以球台的中轴线为 $x$ 轴， $O A$ 所在直线为 $y$ 轴，建立平面直角坐标系，若把球看成点，球从 $A$ 点射出，其运行的高度 $y (m)$ 与运行的水平距离 $x (m)$ 满足函数关系式 $y = a {(x - 1)}^{2} + 0.6$ ．已知球网与 $O$ 点的水平距离为 $1.2 m$ ，高度为 $0.15 m$ ，球台边界距 $O$ 点的水平距离为 $2.6 m$ ．

(1)、求 $y$ 与 $x$ 的函数关系式；

(2)、球能否越过球网？球会不会出界？请说明理由；

(3)、保持发球角度、速度不变的情况下，将发球机调低 $0.2 m$ 后（抛物线形状不变），球从 $B$ 点射出，球越过球网且没有出界，求此时球的落点与 $O$ 点的水平距离．

查看解析

19、综合与实践：在数学活动课中，老师组织同学们分小组测量学校旗杆的高度（学校旗杆底部有基座，经测量，基座高于运动场水平面

1.4 m

），确定以下两种测量方案（见表）．

课题	测量学校旗杆 $A B$ 高度
成员	组长：xxx组员：xxx，xxx，xxx
测量方案名称	标杆方案	测角仪方案
测量工具	卷尺、标杆	卷尺、可调节支架的测角仪
测量示意图
实施过程	①选取运动场与旗杆相距一定距离的 $F$ 处； ②在 $F$ 处站直看旗杆顶，调整标杆 $C D$ 的位置，使标杆顶点 $C$ 与旗杆顶点 $A$ 在同一视线上； ③测量 $D F$ ， $G H$ 的距离，测量标杆 $C D$ 的长度，测量人眼到地面的高度 $E F$ ．	①在运动场与旗杆底部相距一定距离的 $F$ 处，调整测角仪支架的高度，使人眼 $E$ 与旗杆底部 $B$ 位于同一水平高度； ②测量旗杆顶 $A$ 的仰角 $∠ A E B$ ； ③将测角仪沿 $E B$ 方向移至 $D$ 处，再次测量旗杆顶 $A$ 的仰角 $∠ A C B$ ； ④测量 $D F$ 的距离．
测量数据	① $D F = 1.4 m$ ；② $G H = 38.6 m$ ； ③ $C D = 2.6 m$ ；④ $E F = 1.6 m$ ．	① $∠ A E B = 42 °$ ；② $∠ A C B = 45 °$ ；③ $D F = 3.2 m$ ．
备注	①图上所有点均在同一平面内； ② $A B$ ， $C D$ 均与地面垂直； ③旗杆底部基座与运动场的高度差 $M N = 1.4 m$ ．	①图上所有点均在同一平面内； ②参考数据： $sin 42 ° \approx 0.67$ ， $cos 42 ° \approx 0.74$ ， $tan 42 ° \approx 0.90$ ．

任务一：说明以上两种方案各自运用的数学知识：“标杆方案”运用的知识是， “测角仪方案”运用的知识是．（请在下列序号中选择一个填入横线中）

①全等三角形 ②相似三角形 ③锐角三角函数 ④勾股定理

任务二：根据以上测量结果，任意选择一种方案，计算旗杆 $A B$ 的高度（结果精确到 $0.1 m$ ），并说明你选择该种方案的理由．

查看解析

20、如图，某工厂与 $A$ ， $B$ 两地有公路和铁路相连．该工厂从 $A$ 地购买1000元/吨的原料运回工厂，加工成8000元/吨的产品运到 $B$ 地．已知公路的运价为 $1.5$ 元/（吨·km），铁路的运价为 $1.0$ 元/（吨·km）．

(1)、从 $A$ 地运回 $m$ 吨原料到工厂，需要的运费是多少？（用含 $m$ 的代数式表示）

(2)、若其中一批原料，从 $A$ 地运回工厂，到加工成产品运到 $B$ 地，两次运输共支出公路运费16500元，铁路运费93000元．这一批原料为多少吨？每吨原料能加工成的产品的重量是多少？

查看解析

上一页 787 788 789 790 791 下一页跳转