相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
1、赛龙舟是端午节的重要习俗之一,凝聚着团结、协作和勇往直前的精神,某地龙舟赛的赛程为500米,A,B两队在同一起点同时出发,已知A队的平均速度是B队的倍,结果A队比B队提前了25秒到达终点,若设B队的平均速度是x米/秒,可列方程为( )A、 B、 C、 D、
-
2、一副直角三角板如图放置,若 , 则的度数为( ).
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、不等式组的解集在数轴上表示为( ).A、
 B、
B、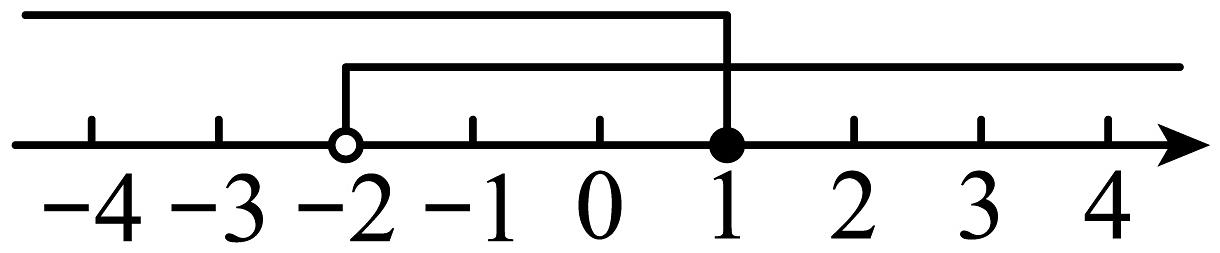 C、
C、 D、
D、
-
4、将“广州中考加油”这六个字分别写在一个正方体的六个面上,此正方体的展开图如图所示,在这个正方体中,与“中”对面的字是( ).
 A、广 B、州 C、加 D、油
A、广 B、州 C、加 D、油 -
5、年某品牌的新能源车在月份的月销量约辆,将用科学记数法可表示为( ).A、 B、 C、 D、
-
6、下列每组数分别是三根小木棒的长度,将它们首尾顺次相接,能摆成三角形的是( )A、3,4,7 B、6,8,15 C、5,12,13 D、5,5,11
-
7、( ).A、1 B、3 C、 D、
-
8、如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,

(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
-
9、已知a、b是正实数,那么,是恒成立的.(1)、由恒成立,请你说明恒成立;(2)、如图,已知是直径,点P是弧上异于点A和点B的一点,连接 , 作 , 垂足为C, , , 由此图说明恒成立.

-
10、为了解学生完成书面作业所用时间的情况,进一步优化作业管理,某中学从全校学生中随机抽取部分学生,对他们一周平均每天完成书面作业的时间(单位:分钟)进行调查.将调查数据进行整理后分为五组:A组“”;B组“”;C组“”;D组“”;E组“”.现将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)、这次调查的样本容量是______,请补全条形统计图;(2)、在扇形统计图中,A组对应的圆心角的度数是______°,本次调查数据的中位数落在_______组内. -
11、解不等式组: , 并写出它的所有整数解.
-
12、若与是同类项,则点关于原点的对称点所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
13、将有理数用四舍五入法精确到千位是( )A、 B、 C、 D、
-
14、下列计算正确的是( )A、 B、 C、 D、
-
15、《九章算术》是我国古代数学的经典著作,奠定了中国传统数学的基本框架,书中记载:“今有大器六、小器一容五斛;大器一、小器六容二斛,问大小器各容几何?”译文:“今有大容器6个、小容器1个,总容量为5斛;大容器1个、小容器6个,总容量为2斛.问大小容器的容积各是多少斛?”

-
16、如图,强大的台风使得一棵大树在离地面6米处折断倒下,大树顶部落在离大树底部8米处,大树折断之前有多高?

-
17、若不等式的解集为 , 则a的取值范围为 .
-
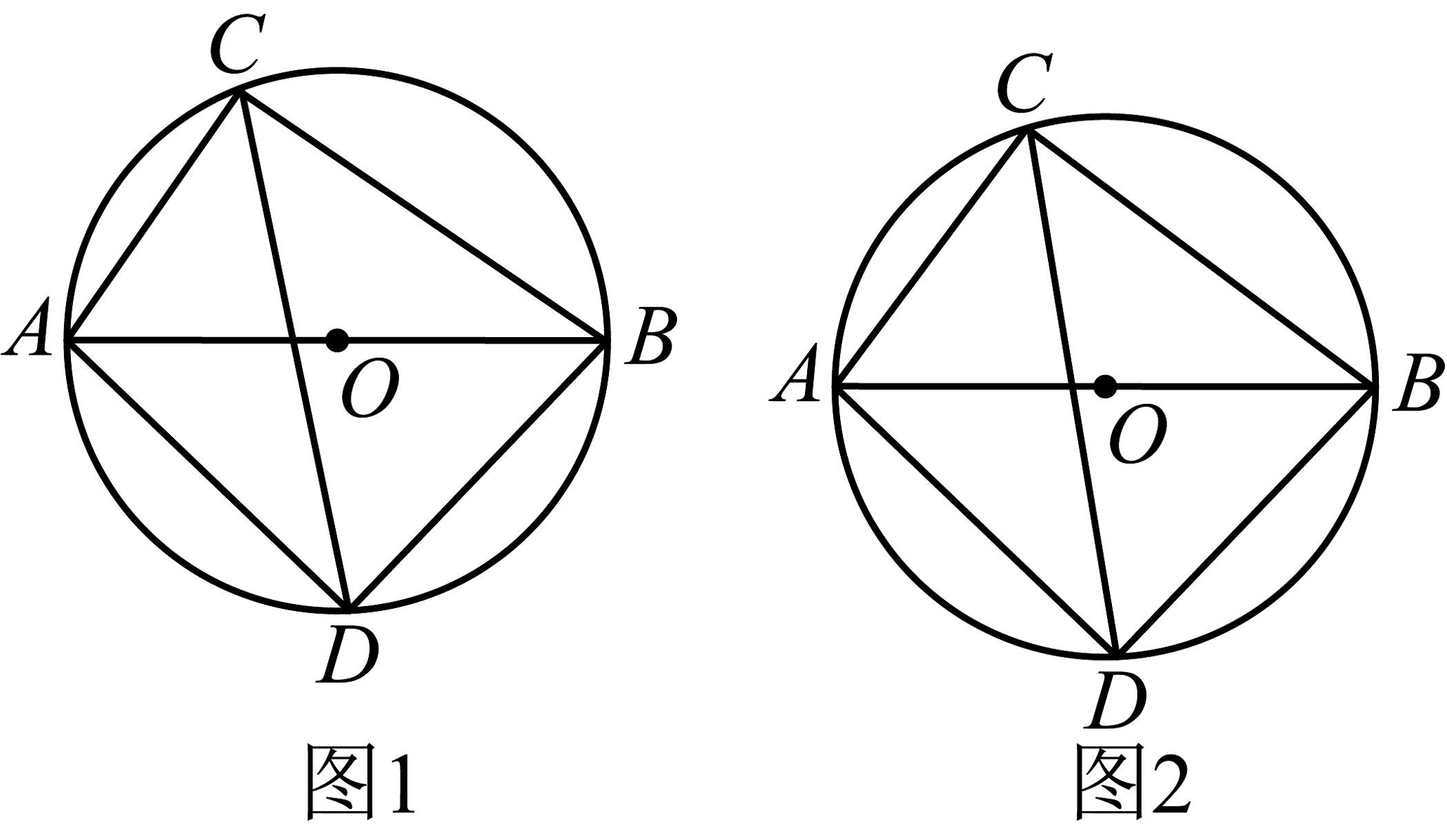
18、回归课本
(1)如图1.的直径为 , 弦为 , 的平分线交于点 , 则______________________ .
深挖问题
(2)在(1)的条件下,求的长.
探究发现
(3)如图2.为的直径,为上的一点(不与点重合),的平分线交于点 , 记 , 请直接写出和之间的数量关系.
-
19、如图,抛物线与轴相交于点 , 与轴相交于点 , , 点是抛物线的顶点.
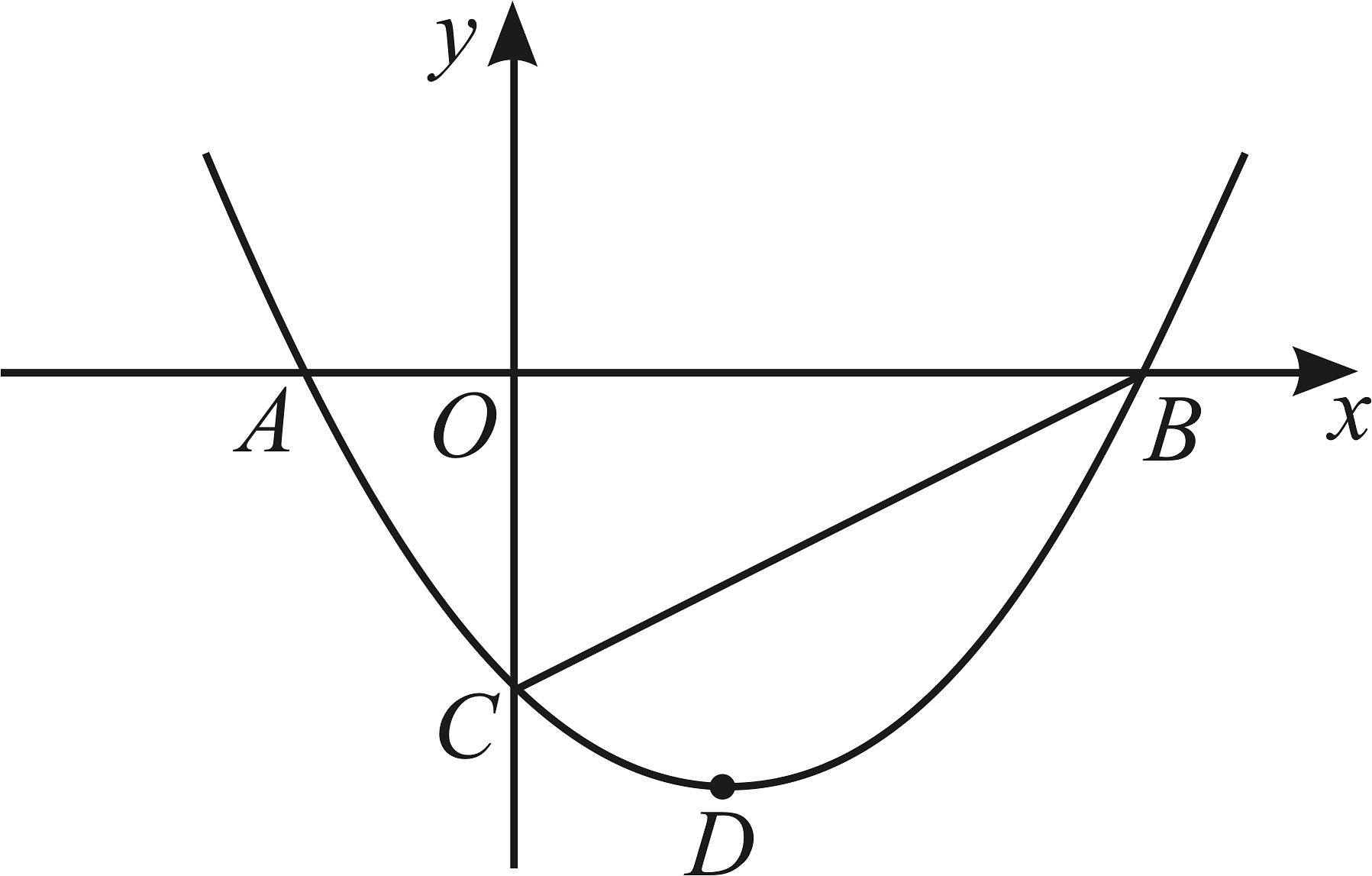 (1)、求抛物线的函数表达式.(2)、在轴上有一点 , 求出的值最小时点的坐标,及此时的值.(3)、在第四象限内的抛物线上是否存在一点 , 过点作轴交轴于点 , 使与相似?若存在,求出点的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式.(2)、在轴上有一点 , 求出的值最小时点的坐标,及此时的值.(3)、在第四象限内的抛物线上是否存在一点 , 过点作轴交轴于点 , 使与相似?若存在,求出点的坐标;若不存在,请说明理由. -
20、图1是某款沙滩椅,图2是该款沙滩椅放置在水平地面上的示意图.已知 , 可通过调试与的夹角来调整靠背高度.
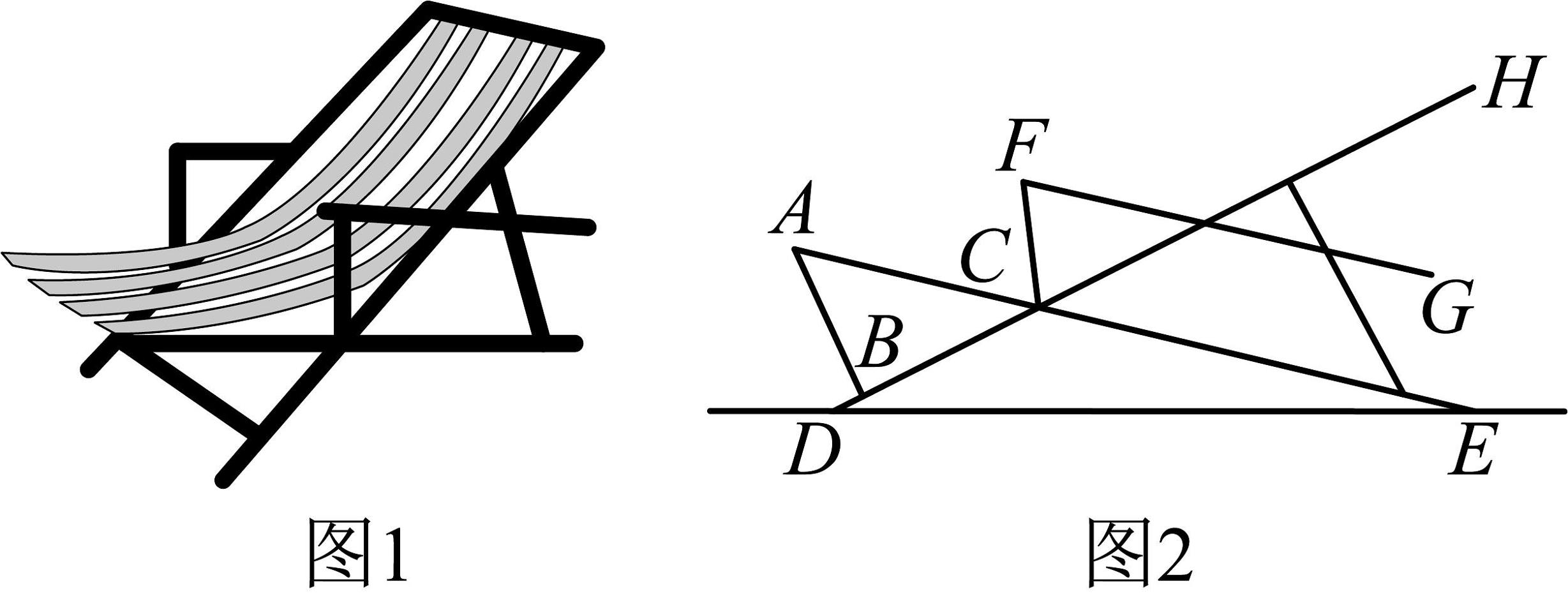 (1)、试判断的形状,并说明理由.(2)、若此时 , 求点到地面的高度.(结果精确到 . 参考数据: , , , , , )
(1)、试判断的形状,并说明理由.(2)、若此时 , 求点到地面的高度.(结果精确到 . 参考数据: , , , , , )