相关试卷

1、若多项式 $2 (m x - \frac{1}{2}) - (x + 5)$ 化简后的结果不含字母x，则m的值为（）

A、 $- 1$ B、0 C、 $\frac{1}{2}$ D、6

查看解析
2、下列方程的解为 $x = - 2$ 的是（）

A、 $\frac{1}{4} x - \frac{1}{2} = 0$ B、 $x + 2 = 0$ C、 $3 x - \frac{1}{6} = 0$ D、 $\frac{1}{2} x - 2 = 0$

查看解析
3、下列说法正确的是（）

A、 $x y^{2}$ 的次数是1 B、 $- \frac{2 v t}{3}$ 的系数是 $\frac{2}{3}$ C、 $x^{2} + 2 x + 18$ 是三次二项式 D、 $\frac{1}{2} a^{2} b - π r^{2}$ 的二次项是 $- π r^{2}$

查看解析
4、中国是最早使用正负数表示相反意义的量的国家．若向东运动 $100 m$ 记作 $+ 100 m$ ，则 $- 200 m$ 表示（）

A、向东运动 $200 m$ B、向西运动 $200 m$ C、向东运动 $100 m$ D、向东运动 $100 m$ （D和C重复了）

查看解析
5、北京是全球首个既举办过夏季奥运会又举办过冬季奥运会的城市．在冬季奥运会前，某赛道计划造雪 $260000 m^{3}$ ．数据260000用科学记数法表示为（）

A、 $260 \times 10^{3}$ B、 $26 \times 10^{4}$ C、 $2.6 \times 10^{5}$ D、 $0.26 \times 10^{6}$

查看解析
6、有理数 $- 4$ ， 0，6， $- \frac{1}{3}$ 中，最小的数是（）

A、 $- 4$ B、0 C、6 D、 $- \frac{1}{3}$

查看解析
7、计算 $5 + (- 12)$ 的结果是（）

A、17 B、 $- 17$ C、7 D、 $- 7$

查看解析
8、方程 $x^{2} - 5 x + 2 = 0$ 的根的存在情况是（）

A、有两个相等的实数根 B、有两个不相等的实根 C、没有实数根 D、无法确定

查看解析
9、小明把一张长方形纸板的四周各剪去一个同样大小的小正方形，如图所示，长方形纸板的长为a，宽为b，小正方形的边长为c．

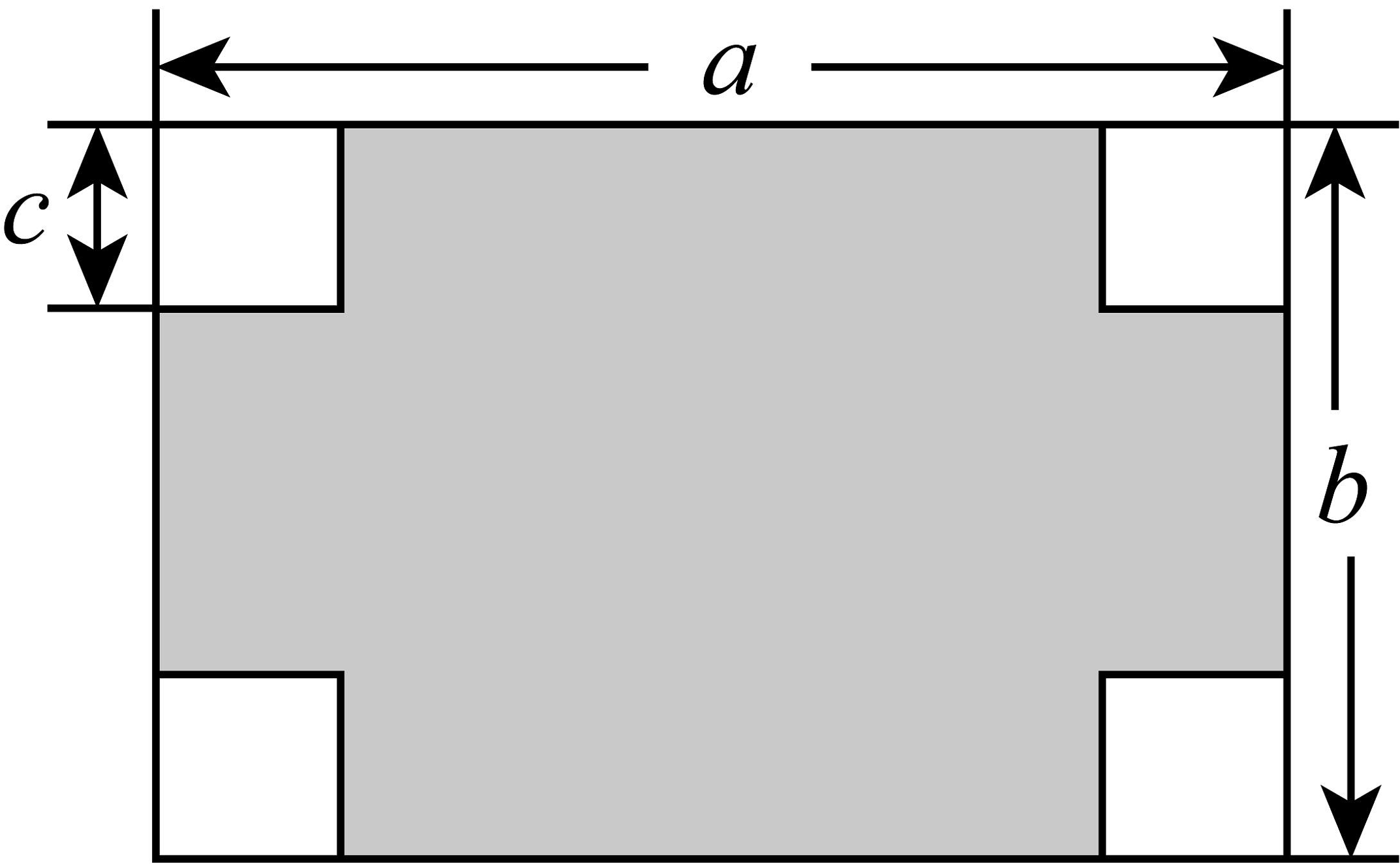(1)、用含a、b、c的代数式表示剩余纸板（阴影部分）的面积．

(2)、当 $a = 20 cm, b = 11 cm, c = 3 cm$ 时，求剩余纸板的面积．

查看解析
10、已知多项式 $x^{2} - (3 k - 1) x y - 3 y^{2} + 3 m x y - 8$ 中不含 $x y$ 项，求 $3 m - 3 k + 2$ 的值．

查看解析
11、计算：

(1)、 $- 1.5 + (- \frac{1}{3}) - (- 2.5) + (- \frac{2}{3})$ ；

(2)、 $(- 3 \frac{1}{2}) + (- \frac{5}{11}) - (+ \frac{1}{3}) + \frac{5}{11}$

(3)、 $(- 36) \times (- \frac{4}{9} + \frac{5}{6} - \frac{7}{12})$

(4)、 ${(- 1)}^{2022} - |1 - 0.5| \times \frac{1}{2} \times [2 - {(- 3)}^{2}]$ ．

查看解析
12、同学们都知道， $|x - 3|$ 表示 $x$ 与 $3$ 的差的绝对值，实际上也可理解为 $x$ 与 $3$ 两数在数轴上所对应的两点之间的距离，同理 $|4 - (- 2)|$ 可理解为 $4$ 与 $- 2$ 两数在数轴上所对应的两点之间的距离，则 $|x - 3| + |x + 5|$ 表示数轴上有理数 $x$ 所对应的点到 $3$ 和 $- 5$ 所对应的两点距离之和．请直接写出 $|x - 3| + |x + 5|$ 的最小值．

查看解析
13、若 $\frac{2}{3} x^{a} y^{3}$ 与 $- 2 x^{2} y^{b}$ 是同类项，则 ${(a - b)}^{2023} =$ ．

查看解析
14、下列说法正确的有（）
①若 $|\frac{1}{a}| = \frac{1}{a}$ ，则 $a > 0$ ；
②若 $|a| > |b|$ ，则有 $(a + b) (a - b)$ 是正数；
③若代数式 $2 x + |9 - 3 x| + |1 - x| + 2011$ 的值与 $x$ 无关，则该代数式值为 $2019$ ；
④代数式 $6 - |x + 1| - |x - 2| - |x + 4|$ 最大值是 $6$ ．

A、1个 B、2个 C、3个 D、4个

查看解析
15、若 $|m - 2| + {(n + 3)}^{2} = 0$ ，则 $m + 2 n$ 的值为（）

A、 $- 4$ B、 $- 3$ C、 $5$ D、 $3$

查看解析
16、点 $A$ 在数轴上表示 $+ 1$ ，把点 $A$ 沿数轴向左平移 $4$ 个单位到点 $B$ ，则点 $B$ 所表示的数是（）

A、 $- 4$ B、 $- 3$ C、 $5$ D、 $- 3$ 或 $5$

查看解析
17、已知抛物线 $y = a x^{2} + b x + 3$ 与x轴相交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与y轴相交于点C．

(1)、求抛物线的解析式；

(2)、在抛物线的对称轴上是否存在一点P，使得 $△ P A C$ 的周长最小，若存在，请求出点P的坐标及 $△ P A C$ 的周长；若不存在，请说明理由；

(3)、在（2）的条件下，在x轴上方的抛物线上是否存在点M（不与C点重合），使得 $S_{△ P A M} = S_{△ P A C}$ ？若存在，请求出点M的坐标；若不存在，请说明理由．

查看解析
18、在平面直角坐标系中， $O$ 为原点，点 $A (- 8, 0)$ ，点 $C (0, 8)$ ，若正方形 $O A B C$ 绕点 $O$ 顺时针旋转，得正方形 $O A^{'} B^{'} C^{'}$ ，记旋转角为 $α$ ．

(1)、如图 $①$ ，当 $α = 45 °$ 时，求 $B C$ 与 $A^{'} B^{'}$ 的交点 $D$ 的坐标；

(2)、如图 $②$ ，当 $α = 30 °$ 时，求点 $B^{'}$ 的坐标；

(3)、若 $P$ 为线段 $B C^{'}$ 的中点，求 $A P$ 长的取值范围（直接写出结果即可）．

查看解析
19、某商场购进一批单价为10元的日用品，若按每件20元的价格销售，每月能卖出20件，若按每件30元的价格销售，每月能卖出10件．假定每月销售件数y（件）与价格x（元/件）之间满足一次函数．

(1)、试求y与x之间的函数关系．

(2)、在不考虑其他因素的条件下，销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？

查看解析
20、如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 150 °$ ，将 $△ A B C$ 绕B点逆时针旋转得到 $△ D B E$ ，旋转角为 $α$ （ $0 ° < α < 180 °$ ），若 $A ， D ， E$ 三点恰好在同一条直线上；

(1)、求旋转角 $α$ 的度数；

(2)、若 $A B = 2$ ，求 $A E$ 的长．

查看解析

上一页 944 945 946 947 948 下一页跳转