相关试卷

1、 $\sqrt{2}$ 与最简二次根式 $4 \sqrt{a - 2}$ 是同类二次根式，则 $a =$ ．

查看解析
2、 $\frac{\sqrt{3}}{2}$ 的相反数是，绝对值是．

查看解析
3、如图，一只蚂蚁从长宽高分别是3，2，6的长方体纸箱的A点沿纸箱表面爬到B点，那么它所行的最短路线的长是（）．

A、 $\sqrt{61}$ B、11 C、7 D、8

查看解析
4、如图，数轴上点P表示的数可能是（）

A、 $\sqrt{7}$ B、 $- \sqrt{7}$ C、 $- 2$ D、 $- 3$

查看解析
5、在﹣ $\sqrt{3}$ 与 $\sqrt{5}$ 之间的整数是（）

A、﹣2，﹣1，0，1，2，3 B、﹣2，﹣1，0，1，2 C、﹣1，0，1，2，3 D、﹣1，0，1，2

查看解析
6、以下三个数，不能组成直角三角形的是（）

A、2，3，4 B、5，12，13 C、3，4，5 D、7，24，25

查看解析
7、图中字母A所代表的正方形的面积是（）．

A、175 B、225 C、400 D、625

查看解析
8、实数 $\frac{π}{2}$ ， $\frac{22}{7}$ ， $0.1414$ ， $\sqrt[3]{9}$ ， $\sqrt{\frac{1}{2}}$ 中，无理数的个数是（）

A、2个 B、3个 C、4个 D、5个

查看解析
9、下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{2}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{0.1}$

查看解析
10、36的算术平方根是（）．

A、 $\pm 6$ B、-6 C、6 D、36

查看解析
11、为响应国家“乡村振兴”的号召，建设绿色生态农村，王大爷承包了一片土地用于种植某品种草莓．如图所示是种植草莓的土地平面示意图（单位：米）

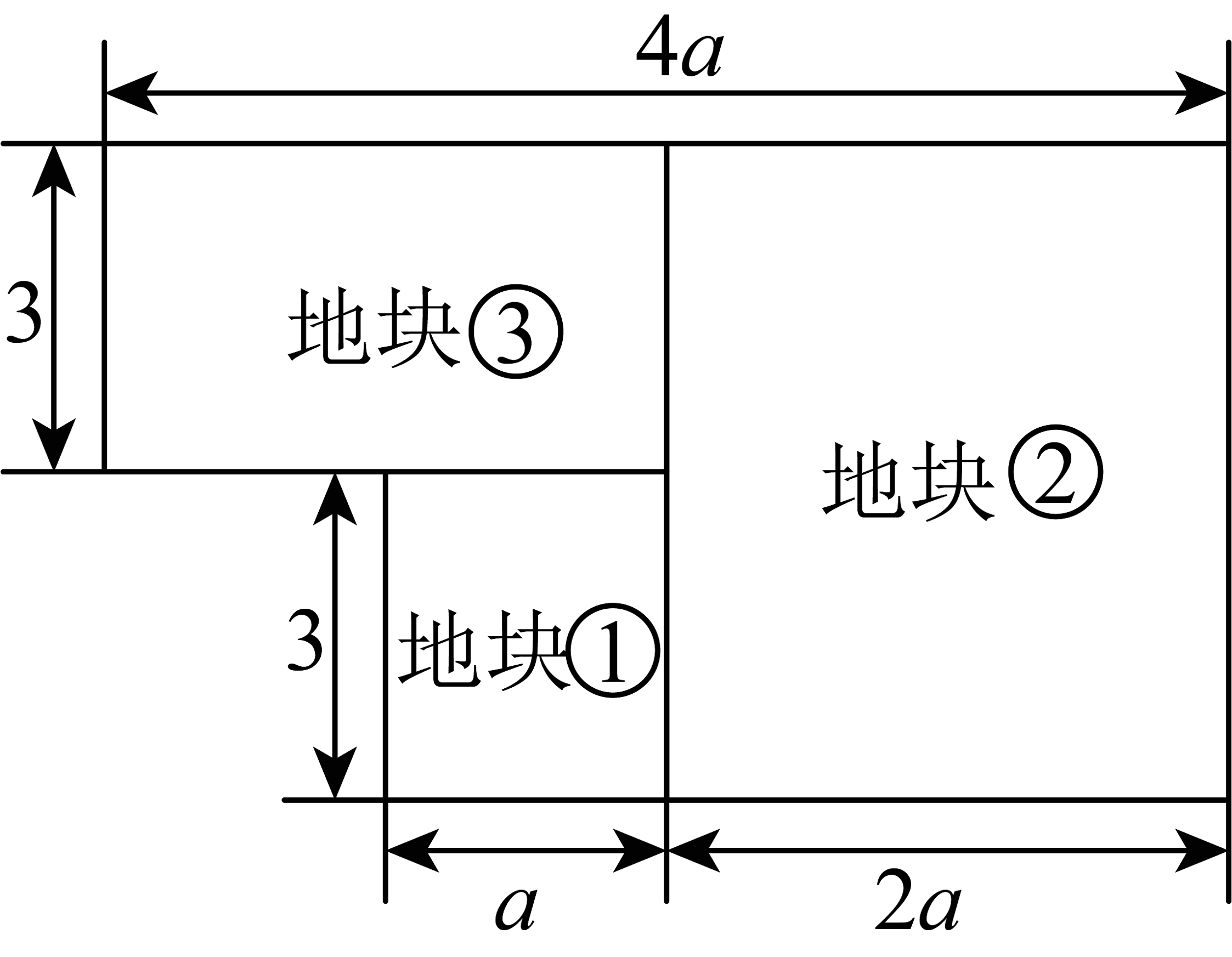(1)、用含 $a$ 的式子表示出这片土地的总面积；

(2)、由于草莓品种和各个地块土壤条件存在差异，地块②平均每平方米可种植2株草莓，剩下地块平均每平方米可种植3株草莓，则当 $a = 5$ 时，王大爷承包的土地一共可以种植多少株草莓？

查看解析
12、已知有理数 $m$ 所表示的点到原点的距离为 $4$ 个单位长度， $a 、 b$ 互为相反数且都不为零， $c 、 d$ 互为倒数．

(1)、求 $m$ 的值．

(2)、求 $m + 2 c d + \frac{a + b}{4 m}$ 的值．

查看解析
13、化简求值： $(2 - 7 x - 6 x^{2} + x^{3}) + (x^{3} + 4 x^{2} + 4 x - 3) - (- x^{2} - 3 x + 2 x^{3} - 1)$ 的值，其中 $x = - \frac{1}{2}$ ．

查看解析
14、计算： $- 1^{4} + [(- 2) \div (- \frac{1}{6}) - (1 - 9) \times 5]$ ．

查看解析
15、将下列各数填入相应的大括号内（无需化简，原式填入）：
$- 7$ ， $|- \frac{1}{7}|$ ， $0$ ， $3.14$ ， $- 30 %$ ， $- (- 2)$ ， $\frac{π}{5}$ ， $1.5$
整数集合：{                                            $\dots$ }；
正有理数集合：{                                            $\dots$ }；
非负整数集合：{                                            $\dots$ }；
负分数集合：{                                            $\dots$ }．

查看解析
16、一个正方体的表面展开图如图所示，六个面上各有一字，连起来的意思是“爱大沥讲文明”，把它折成正方体后，与“大”相对的字是（）

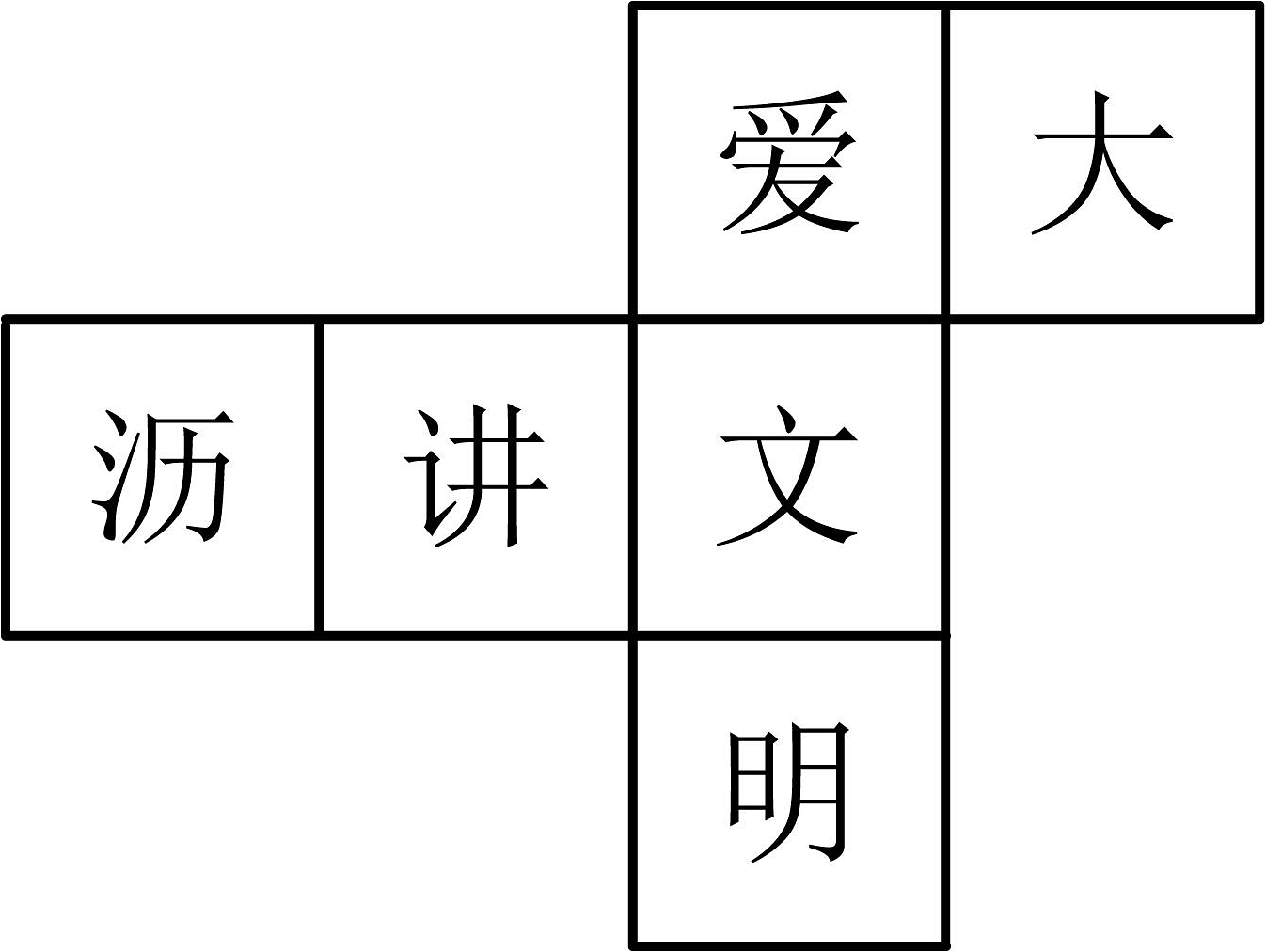A、沥 B、讲 C、文 D、明

查看解析
17、如图，在四边形 $A B C D$ 中 $, A B = A D, E, F$ 分别是 $B C, C D$ 上的点，且 $E F = B E + F D$ ．

(1)、如图1，若 $∠ B = ∠ A D C = 90 °$ ，求 $∠ B A E, ∠ F A D, ∠ E A F$ 之间的数量关系．小明的方法是：延长 $F D$ 到点 $H$ ，使 $D H = B E$ ，连接 $A H$ ，先证明 $△ A B E ≌ △ A D H$ ，再证明 $△ A E F ≌ △ A H F$ ，最后可得出结论：______．

(2)、如图2，若 $∠ B + ∠ D = 180 °$ ，其他条件不变，（1）中的结论是否仍然成立？请说明理由．

(3)、如图3，若 $∠ A B C + ∠ A D C = 180 °$ ，点 $E$ 在 $C B$ 的延长线上，点 $F$ 在 $C D$ 的延长线上，其他条件不变，求 $∠ F A E$ 与 $∠ D A B$ 之间的数量关系．

查看解析
18、阅读下列分解因式的过程：
$1 + x + x (1 + x) + x {(1 + x)}^{2}$ $= (1 + x) + x (1 + x) + x {(1 + x)}^{2}$
$= (1 + x) [1 + x + x (1 + x)]$ $= (1 + x) [(1 + x) + x (1 + x)]$
$= {(1 + x)}^{2} (1 + x)$ $= {(1 + x)}^{3}$ ．
根据上述分解因式的过程，回答下列问题：

(1)、上述过程中用到的分解因式的方法是______，共应用了______次；

(2)、分解因式： $1 + x + x (1 + x) + x {(1 + x)}^{2} + x {(1 + x)}^{3} + \cdot \cdot \cdot + x {(1 + x)}^{2024}$ ；

(3)、若要分解因式 $1 + x + x (1 + x) + x {(1 + x)}^{2} + x {(1 + x)}^{3} + \cdot \cdot \cdot + x {(1 + x)}^{n}$ （ $n$ 为正整数），则需应用上述方法______次，分解因式的结果是______．

查看解析
19、如图，四边形 $A B C D$ 、 $C E F G$ 均为正方形，其中正方形 $C E F G$ 面积为 $36 {cm}^{2}$ ，若图中阴影部分面积为 $10 {cm}^{2}$ ，求正方形 $A B C D$ 的面积．

查看解析
20、小明有一个大正方体铁块，其体积为 $125 {cm}^{3}$ ．

(1)、求这个大正方体铁块的棱长；

(2)、小明要将这个大正方体铁块熔化，重新锻造成两个小正方体铁块，其中一个小正方体铁块的体积为 $98 {cm}^{3}$ ，求另一个小正方体铁块的棱长．

查看解析

上一页 865 866 867 868 869 下一页跳转