-
1、某校举行“珍爱生命”演讲比赛,已知某位选手的“演讲内容”、“语言表达”和“形象风度”这三项得分分别为90分,85分,80分,若按的比例计算平均得分,则该选手的平均得分是( )A、85分 B、86分 C、87分 D、88分
-
2、【感悟】如图1,是的高线, , 若 , , 求的长.
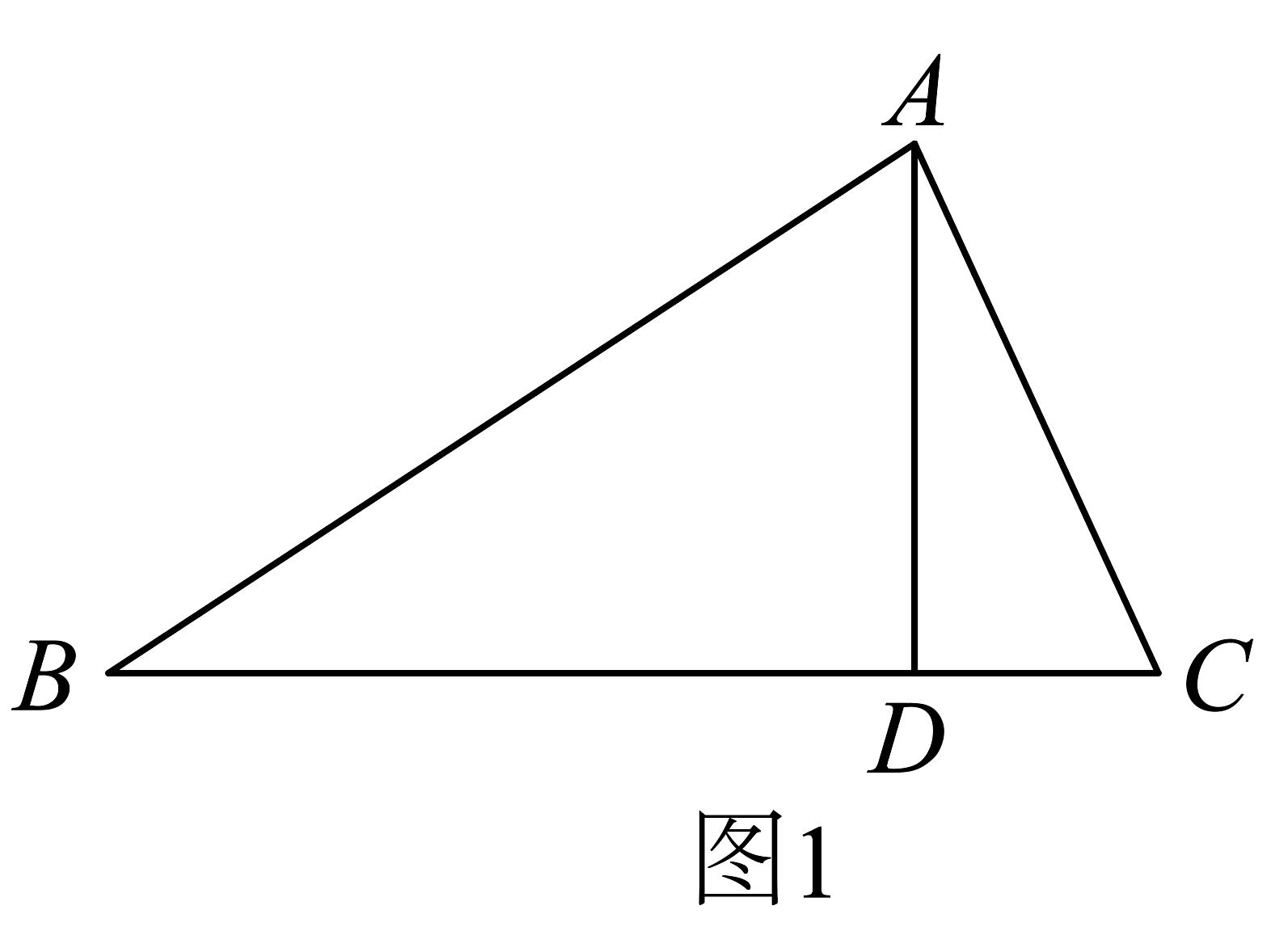
小明同学的思路是:将沿折叠,点刚好落在边上的点处.请你根据小明的思路直接写出_________.
【探究】如图2, , 为的外角的平分线,交的延长线于点 , 则线段、、又有怎样的数量关系?请写出你的猜想并证明.
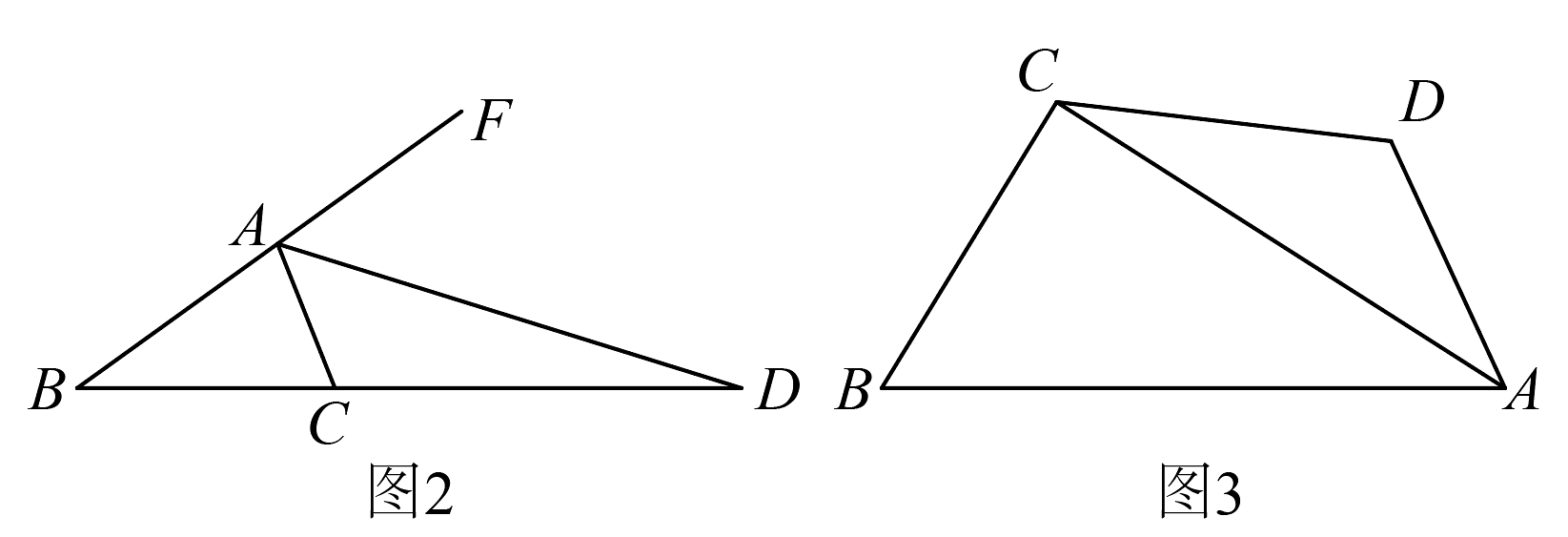
【拓展】如图3,在四边形中,平分 , , .
①求证:;
②若 , 则的长为_____________.
-
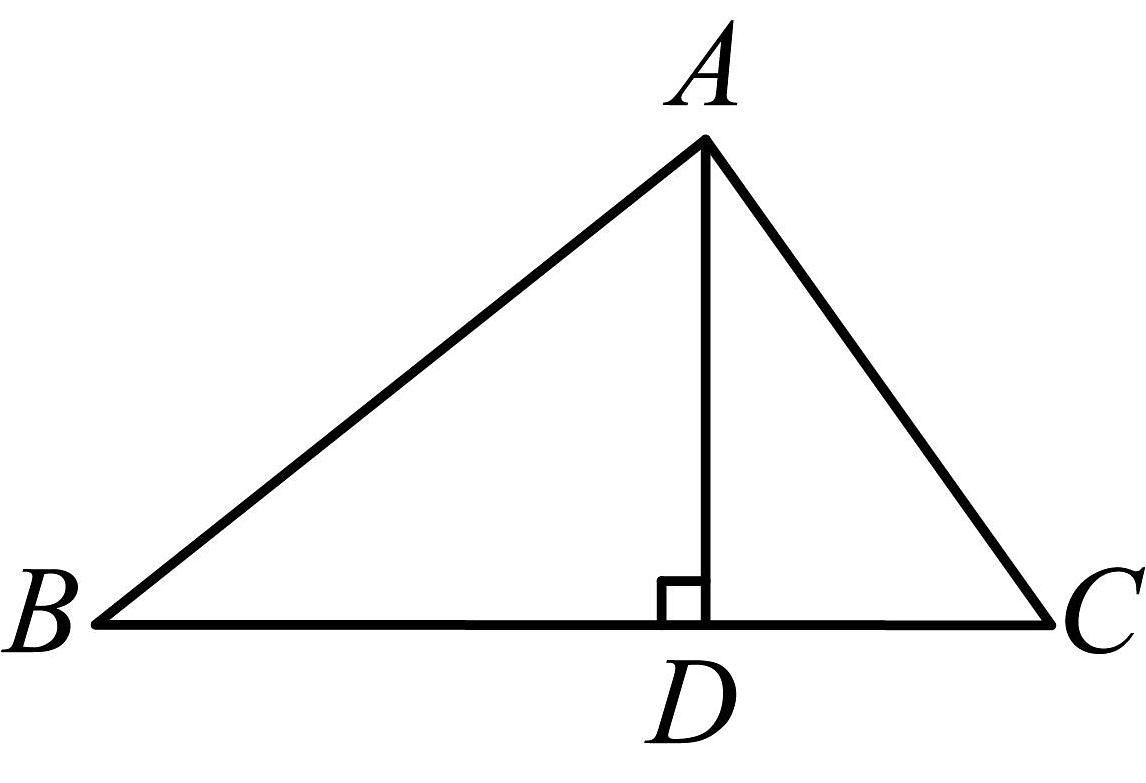
3、在学校组织的研学活动中,需要学生自己搭建帐篷.下图是搭建帐篷的示意图.在中,支架从帐篷顶点支撑在水平的支架上,且于点 , 经测量得: , , . 按照要求,帐篷支架与所夹的角需为直角.请通过计算说明学生搭建的帐篷是否符合条件.
-
4、阅读下面的内容.
比较与的大小
“嘉嘉”的思路:
将 , 两个式子分别平方后,再进行比较.
“淇淇”的思路:
以、 , 为三边构造一个 , 再利用三角形的三边关系进行比较.
请利用嘉嘉、淇淇的思路分别进行说明.
-
5、已知一个底面为正方形的长方体,高是底面边长的2倍,体积为 . 求:(1)、这个长方体的底面边长;(2)、这个长方体的表面积.
-
6、如图,在中, , 是边的垂直平分线,连接 .
 (1)、若 , 求的长;(2)、若平分 , 求的度数.
(1)、若 , 求的长;(2)、若平分 , 求的度数. -
7、已知 , 且 , , , 点、分别在、上滑动.
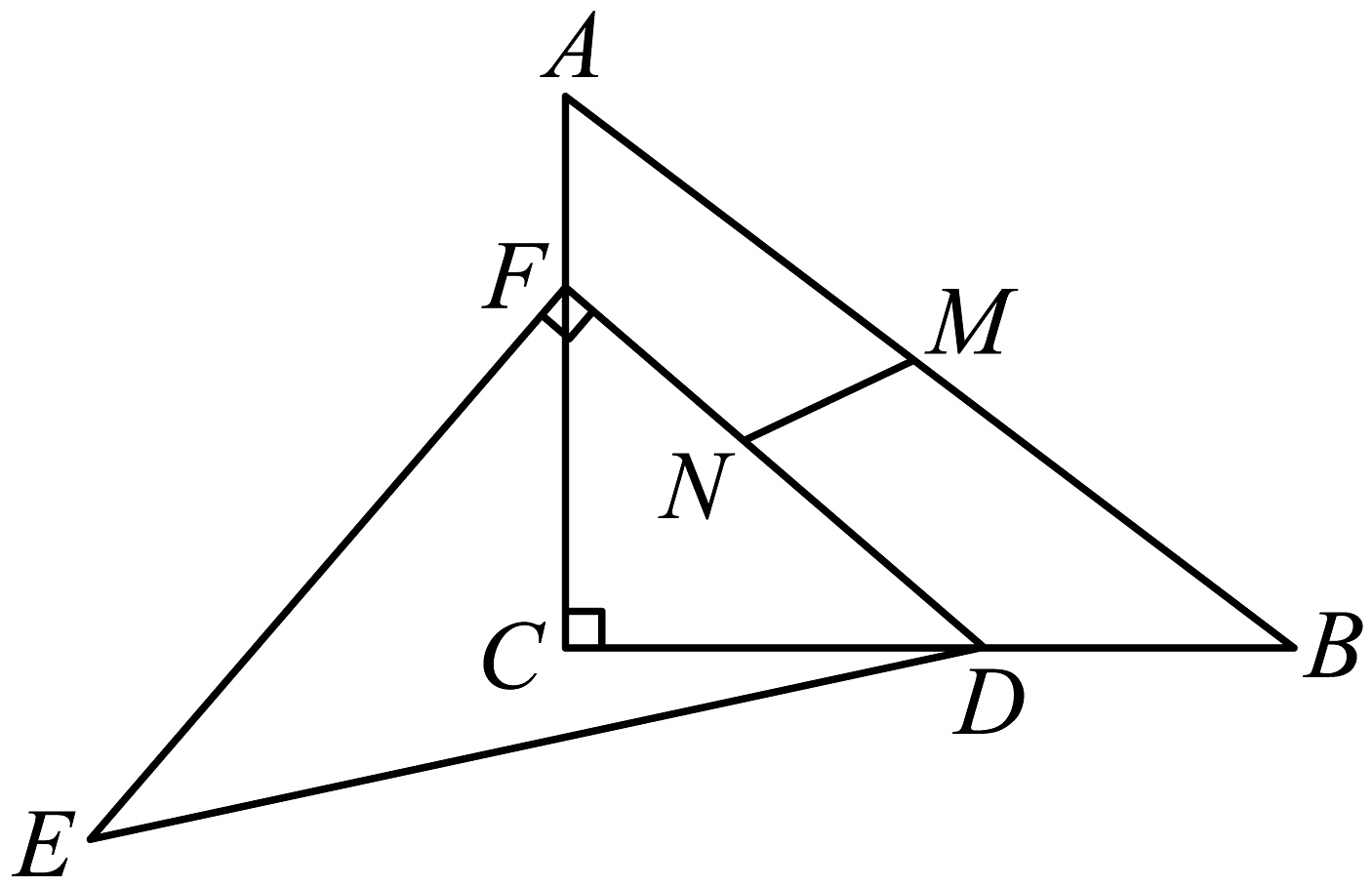
(1);
(2)点是的中点,点是的中点,则的最小值是 .
-
8、如图, , 点A在上,且 , 按下列要求画图:
以A为圆心,1为半径向右画弧,交于点A1 , 得到第1条线段 .
以为圆心,1为半径向右画弧,交于点 , 得到第2条线段 .
以为圆心,1为半径向右画弧,交于点 , 得到第3条线段 .
……这样画下去,直到第条线段,之后就不能再画出符合要求的线段了,则( )
 A、15 B、14 C、13 D、12
A、15 B、14 C、13 D、12 -
9、如图,、E是直线上不重合的两点,是的角平分线,于点A,若的周长为10,则的周长可能是( )
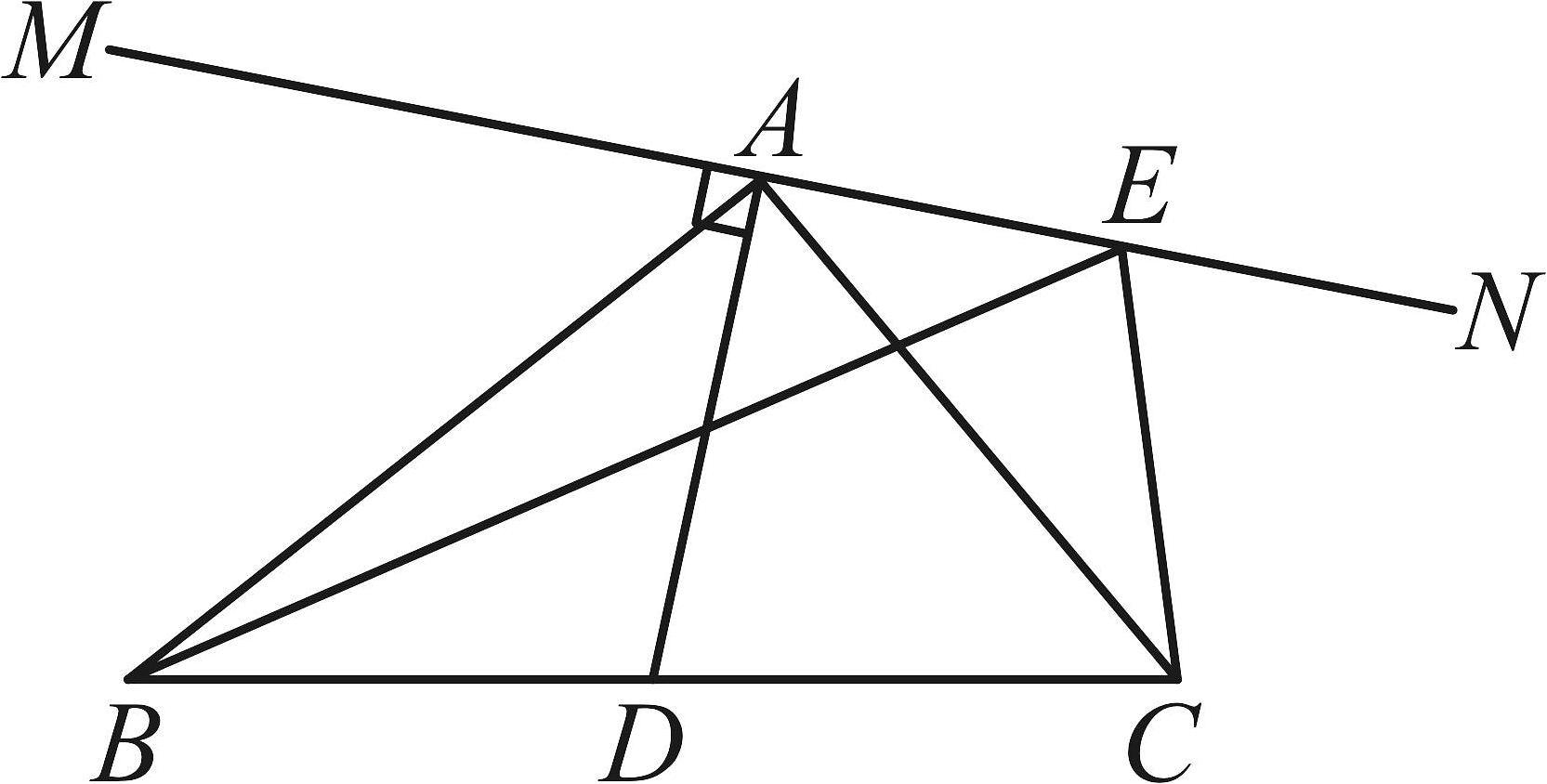 A、8 B、9 C、10 D、11
A、8 B、9 C、10 D、11 -
10、小明在纸上书写了一个正确的演算过程,同桌小亮一不小心撕坏了一角,如图所示,则撕坏的一角中“”为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,根据尺规作图痕迹,图中标注在点A处所表示的数为( )
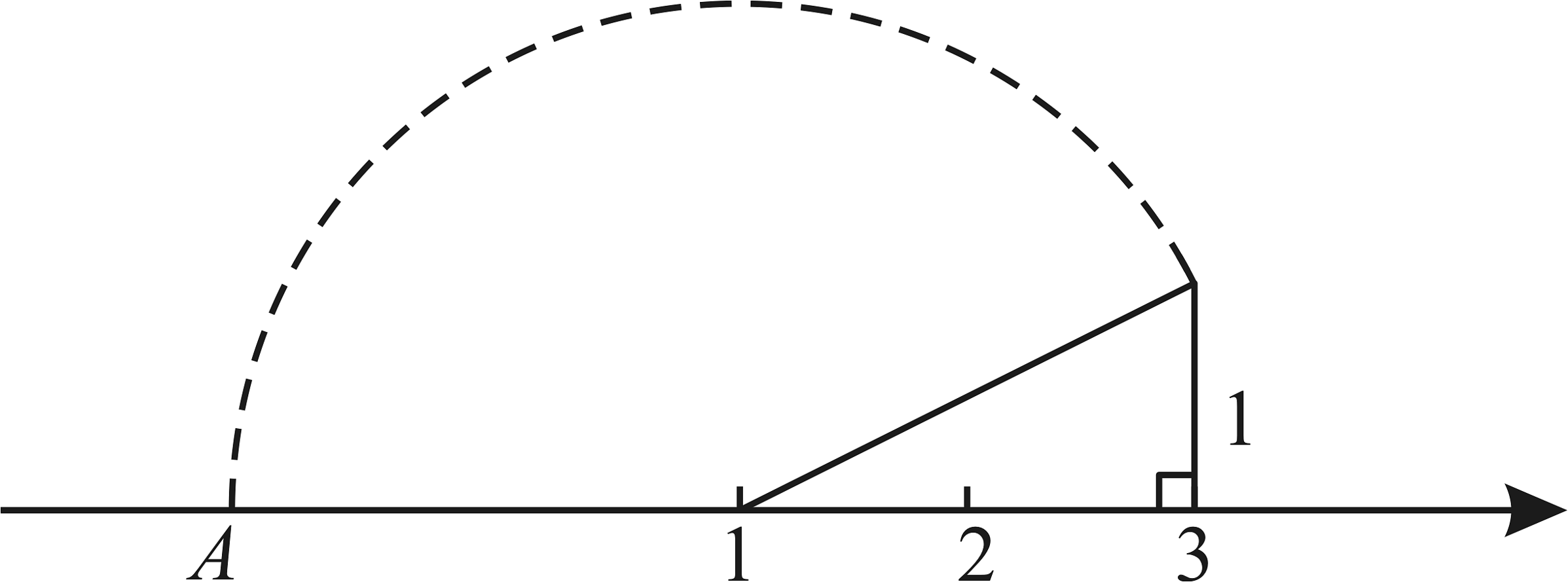 A、 B、 C、 D、
A、 B、 C、 D、 -
12、某班开展“用直尺和圆规作角平分线”的探究活动,甲、乙两个同学展示作图痕迹如下,其中射线为平分线的是( )
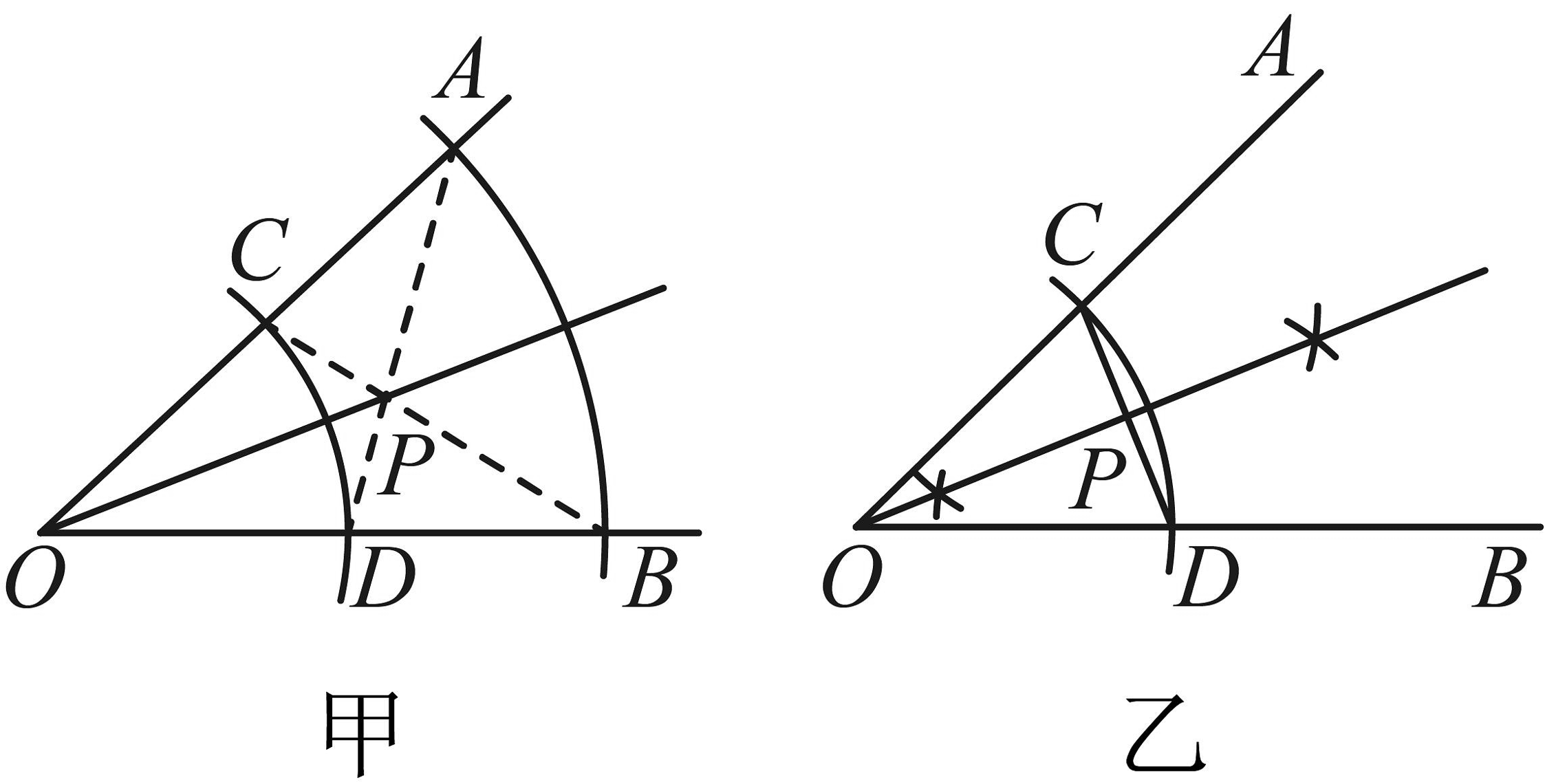 A、甲 B、乙 C、甲和乙 D、甲、乙均不是
A、甲 B、乙 C、甲和乙 D、甲、乙均不是 -
13、的平方根是( )A、2 B、4 C、 D、
-
14、甲、乙、丙三人进行乒乓球比赛赛前训练,每局两人进行比赛,第三个人做裁判,每一局都要分出胜负,胜方和原来的裁判进行新一局的比赛,输方转做裁判,依次进行.半天训练结束时,发现A共当裁判9局.
①若B,C分别进行了17局,13局比赛,则这半天训练中,三人共进行了局比赛;
②三人至少进行了局比赛.
-
15、已知抛物线G:有最低点.
(1)求二次函数的最小值(用含m的式子表示);
(2)将抛物线G向右平移m个单位得到抛物线G1 . 经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(3)记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围.
-
16、如图是由连续的奇数1,3,5,7,……排成的数阵,用如图所示的字框框住其中的四个数,设竖列中间的数为 , 则这四个数的和为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、已知光的速度约为 , 太阳光射到地球上需要的时间约为 , 则地球与太阳间的距离约为多少千米?用科学记数法表示为( )A、 B、 C、 D、
-
18、如图,中, , 点D在边上,且交于点E.
 (1)、求证:;(2)、若 , E是中点,求的长.
(1)、求证:;(2)、若 , E是中点,求的长. -
19、如图, , 直角顶点C,E在x轴上,点A,D的坐标分别是 , , 则点B的坐标是 .

-
20、甲、乙两位同学将两张全等的直角三角形纸片进行裁剪和拼接,尝试拼成一个尽可能大的正方形.
要求:①直角三角形纸片的两条直角边长分别为和;
②在两张直角三角形纸片中各裁剪出一个图形,使它们的形状和大小都相同;
③将这两个图形无缝隙拼成一个正方形,正方形的边长尽可能大.
甲同学的方案
乙同学的方案


请根据以上信息,完成下列问题:
(1)、甲同学的方案中,拼成的正方形边长是________;(2)、求出乙同学方案中拼成的正方形的边长;(3)、以上两个同学的方案中,________(填“甲”或“乙”)拼成的正方形边长大;(4)、请你设计一个新方案,使拼成的正方形的边长比甲、乙两位同学拼成的正方形都大.(要求:在答题卷上的两个直角三角形中分别画出裁剪线并直接写出这个正方形的边长)