-
1、 如图, , 点P是的角平分线上一点,且点P在之间,连结 , 设 . 当 , 时,求的度数.

-
2、 分解因式:(1)、 .(2)、 .(3)、 .
-
3、 计算:(1)、 .(2)、 .(3)、 .(4)、 .
-
4、 有两张正方形纸片 , 其中 . 若将这两个正方形纸片按图(1)所示的方式放置(点B和点F重合),产生了一个新的、周长为8的正方形 . 若将这两个正方形纸片按图(2)所示并排放置,其中,点B和点E重合,点A , B , F在同一条直线上,点P是线段的中点.连接 , 若三角形的面积是3.则图(2)中阴影部分的面积是 .

-
5、 已知 , 其中m , n为互不相等实数,且满足 , 则 . (结果用只含a的代数式表示)
-
6、 如图,将一块三角尺沿着方向平移到三角尺的位置,其中,点A的对应点为点D , 连接 . 若 , , 则 .

-
7、 设 , , . 若 , , 则 .
-
8、 在一个样本中,50个数据分别落在5个组内,其中第一、二、四、五组的频率之和为 , 则第三组的频数为 .
-
9、 对于代数式 , 小滨分别计算当 , 2,3,4时该代数式的值,得到以下四个结论:①;②;③;④ . 小江发现其中有且只有一个结论是错误的,则错误的结论是( )A、① B、② C、③ D、④
-
10、 将一条两边互相平行的纸带()按如图方式折叠,折痕分别为 , , 且满足 . 若增大 , 则( )
 A、增大 B、增大 C、减小 D、减小
A、增大 B、增大 C、减小 D、减小 -
11、 某家具厂设计的餐桌椅套装,1张桌子配4把椅子.该厂一天能生产桌子17张或椅子32把,决定用25天时间生产一批这样的餐桌椅,其中,安排x天只生产桌子,剩余y天只生产椅子.若使生产的桌子和椅子恰好配套,则可列方程组( )A、 B、 C、 D、
-
12、 若实数x满足 , 则的值为( )A、2025 B、2026 C、2027 D、2028
-
13、 在同一平面内,有三条不重合的直线a , b , c , ( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则
-
14、 下列等式变形中,正确的是( )A、 B、 C、 D、
-
15、 当时,下列代数式的值最小的是( )A、 B、 C、 D、
-
16、 若是二元一次方程的一个解,则( )A、0 B、1 C、2 D、3
-
17、 要使分式有意义,则x的取值需满足( )A、 B、 C、或 D、且
-
18、 要了解某校学生每周体育锻炼的时间,下列选取调查对象的方式最合适的是( )A、随机选取一个体育队的学生 B、在全校学生中随机选取100人 C、随机选取一个班的学生 D、在全校男生中随机选取100人
-
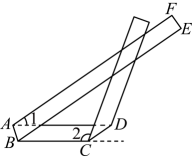
19、如图,将绕点逆时针旋转得到 , 若点落在线段的延长线上,则大小为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、如图,在长、宽的长方形花园中,欲修宽度相等的观赏路(如图中阴影部分),要使空白部分面积是 , 若设路宽为 , 则x应满足的方程是
 A、 B、 C、 D、
A、 B、 C、 D、