相关试卷

1、如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $D E$ 垂直平分 $A B$ ，连接 $A E$ ．

(1)、证明： $∠ A E C = 2 ∠ B$ ．

(2)、若 $∠ B A C = 60 °$ ， $E C = 3$ ，求 $B E$ 的长．

查看解析
2、在 $△ A B C$ 中，P是 $B C$ 边上的一点，过点P作 $B C$ 的垂线，交 $A B$ 于点Q，交 $C A$ 的延长线于点R．若 $A Q = A R$ ，求证： $△ A B C$ 是等腰三角形．

查看解析
3、已知： $x y = 2$ ， $x + y = 4$ ，求 $x^{2} y + x y^{2} - x^{2} y^{2}$ 的值

查看解析
4、计算：

(1)、 $- 2 a^{2} (3 a b^{2} - 5 a b^{3})$

(2)、 $(a + 2 b) (a - 2 b)$

(3)、 $(24 x^{4} - 6 x^{2} + 3 x) \div 3 x$

查看解析
5、观察下列关于x的单项式，探究其规律： $3 x, \frac{5}{2} x^{2}, \frac{7}{3} x^{3}, \frac{9}{4} x^{4}, \frac{11}{5} x^{5}, \frac{13}{6} x^{6}$ ， ……，按照上述规律，第2024个单项式是（）

A、 $\frac{4046}{2023} x^{2023}$ B、 $\frac{4047}{2023} x^{2023}$ C、 $\frac{4049}{2024} x^{2024}$ D、 $\frac{4045}{2024} x^{2024}$

查看解析
6、昆明市打算在某条街道新建一所中学，为了方便居民区A、B的学生上学，要使A、B两小区到学校的距离之和最小，则学校C的位置应该在（）

A、 B、 C、 D、

查看解析
7、为了丰富学生的课外活动，在周一班会课中，班主任张老师设置抢凳子游戏，有A、B、C三名选手站在一个三角形的三个顶点位置上，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在 $△ A B C$ 的（）

A、三边中线交点 B、三条角平分线交点 C、三边垂直平分线的交点 D、三边上高的交点

查看解析
8、如图，生物课堂中，同学们在显微镜下观察某树叶的细胞图片，一个细胞可近似看成如图多边形，则该多边形的内角和是（）

A、 $1080 °$ B、 $720 °$ C、 $1440 °$ D、 $900 °$

查看解析
9、若三角形两边长分别是3、5，则第三边的长可能是（）

A、2 B、3 C、10 D、11

查看解析
10、巴黎奥运会已在2024年8月11日落下帷幕，但是运动健儿在奥运赛场上的拼搏精神仍牢记我们心中，下列运动项目的图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看解析
11、观察下列各式：
$1 - \frac{1}{2^{2}} = \frac{3}{4} = \frac{1}{2} \times \frac{3}{2}$ ； $1 - \frac{1}{3^{2}} = \frac{8}{9} = \frac{2}{3} \times \frac{4}{3}$ ； $1 - \frac{1}{4^{2}} = \frac{15}{16} = \frac{3}{4} \times \frac{5}{4}$ ； $1 - \frac{1}{5^{2}} = \frac{24}{25} = \frac{4}{5} \times \frac{6}{5}$ ；…．

(1)、用你发现的规律填写下列式子的结果： $1 - \frac{1}{10^{2}} = \frac{()}{100} = \frac{()}{10} \times \frac{()}{10}$ ；

(2)、用你发现的规律计算： $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times (1 - \frac{1}{2}) \times \dots \times (1 - \frac{1}{100^{2}})$ ．

查看解析
12、用“ $△$ ”定义新运算：对于任意有理数 $a ， b$ ，当 $a \leq b$ 时，都有 $a △ b = a^{2} \times b$ ；当 $a > b$ 时，都有 $a △ b = a \times b^{2}$ ．

(1)、求 $2 △ 6$ 的值；

(2)、定义一种运算，就要研究它的运算律：
①求 $(- 1) △ (- 3)$ 和 $(- 3) △ (- 1)$ 的值；
②这个计算结果说明了这个运算满足律．

查看解析
13、有理数 $a ， b ， c$ 在数轴上的位置如图所示：

(1)、请在数轴上标出 $- a ， - b ， - c$ ；

(2)、比较 $a ， b ， c ， - a ， - b ， - c$ 的大小（用“ $<$ ”将它们连接起来）．

查看解析
14、计算：

(1)、 $8 - \frac{1}{4} - 5 - (- 0.25)$ ；

(2)、 $1 - \frac{1}{8} \div (\frac{1}{2} - \frac{7}{8}) \times (- \frac{1}{3})$ ；

(3)、 $- 3^{2} \times (- 2 \frac{1}{4}) \div (- \frac{1}{2}) \times 2$ ．

查看解析
15、如图所示的是一个简单的数值运算程序．当输入 $x$ 的值为4时，输出的值为．

查看解析
16、绝对值大于3且小于5的所有整数的和是．

查看解析
17、下列用四舍五入法分别取近似数，其中错误的是（）

A、0.1（精确到0.1） B、0.05（精确到百分位） C、8.12亿（精确到百分位） D、 $5.24 \times 10^{7}$ （精确到十万位）

查看解析
18、下列各式中计算正确的是（）

A、 $- \frac{5}{7} + \frac{2}{7} = - (\frac{5}{7} + \frac{2}{7}) = - 1$ B、 $- 5 - 2 = - (5 - 2) = - 3$ C、 $3 \div \frac{5}{4} \times \frac{4}{5} = 3 \div 1 = 3$ D、 $- 2^{2} = - 4$

查看解析
19、有理数a，b在数轴上的对应点的位置如图所示，在 $a + b ， a - b ， a b ， |a| - |b|$ 中，正数有（）

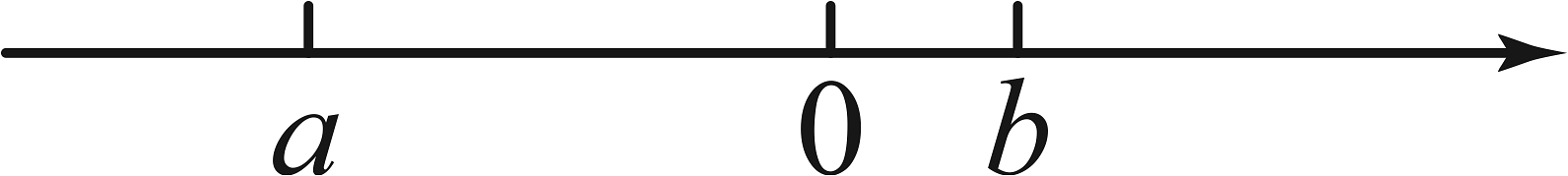A、1个 B、2个 C、3个 D、4个

查看解析
20、下列式子一定成立的是（）

A、 ${0.1}^{2} = 2$ B、 $- 2^{4} = 16$ C、 $|- 2^{3}| = 8$ D、 ${(- 1)}^{2024} = - 1$

查看解析

上一页 1135 1136 1137 1138 1139 下一页跳转