相关试卷

1、定义一种新运算“△”： $a △ b = b^{2} - a b$ ，例如： $1 △ (- 2) = {(- 2)}^{2} - 1 \times (- 2) = 4 + 2 = 6$ ．计算：

(1)、 $(- 3) △ (- 5)$ ；

(2)、 $[(- \frac{1}{2}) △ 4] △ \frac{1}{3}$ ．

查看解析
2、计算：

(1)、 $(- 2) \times 4 - 18 \div (- \frac{1}{2})$ ；

(2)、 ${(- 1)}^{10} + 5 - (1 - \frac{1}{6}) \times 12$ ．

查看解析
3、将下列各数填入它所属的集合内： $+ 6$ ， $- 18$ ， 2024， $- 3.14$ ， 0， $95 %$ ， $\frac{22}{7}$ ， $- 1.8$ ， $- \frac{3}{5}$ ， $0. \dot{6} \dot{7}$ ．

(1)、正有理数集合：{                       …}．

(2)、负有理数集合：{                       …}．

(3)、整数集合：{                            …}．

查看解析
4、贵阳市黔灵山公园于2024年1月1日起向公众免费开放．据统计，免费开放当日接待游客约45000人次.45000这个数用科学记数法表示应为．

查看解析
5、鸡蛋的最佳孵化温度是在 $37.8 ℃$ 左右，若低于最佳孵化温度 $0.5 ° C$ 记作 $- 0.5 ° C$ ℃，则高于最佳孵化温度 $0.5 ° C$ 应该记作．

查看解析
6、已知a是最大的负整数，b是绝对值最小的数，c是倒数等于其本身的数．则这三个数的和为（）

A、 $- 2$ 或0 B、0或2 C、1或3 D、 $- 1$ 或1

查看解析
7、某快递驿站将收到的快件数记为正数，取走的快件数记为负数，其近三天的快件进出情况如表所示，表中星期四的数据被墨水污染了，请你算出星期四快件的进出数为（）
星期三
$+ 8$
星期四
■
星期五
$- 14$
三天合计
$+ 3$

A、 $- 3$ B、 $+ 3$ C、 $- 9$ D、 $+ 9$

查看解析
8、在数轴上与表示 $- 1$ 的点的距离为10个单位长度的点表示的数是（）

A、11 B、9 C、 $- 9$ 或11 D、9或 $- 11$

查看解析
9、下列说法正确的是（）

A、3.14不是分数 B、不带“ $-$ ”号的数都是正数 C、0是自然数也是正数 D、有理数分为正有理数、0和负有理数

查看解析
10、如图，在数轴上每隔一个单位长度取一个点，若点A表示的数是 $- 3$ ，则点B表示的数是（）

A、0 B、1 C、2 D、3

查看解析
11、一种小吃包装袋上标注着“净含量： $50 g \pm 1 g$ ”，则下列小吃净含量合格的是（）

A、52 B、48 C、50.5 D、51.5

查看解析
12、 $- \frac{1}{2}$ 的绝对值是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $- 2$ D、2

查看解析
13、若关于x的一元二次方程 $k x^{2} - 6 x + 1 = 0$ 有两个相等的实数根，则k的值是．

查看解析
14、综合与实践：
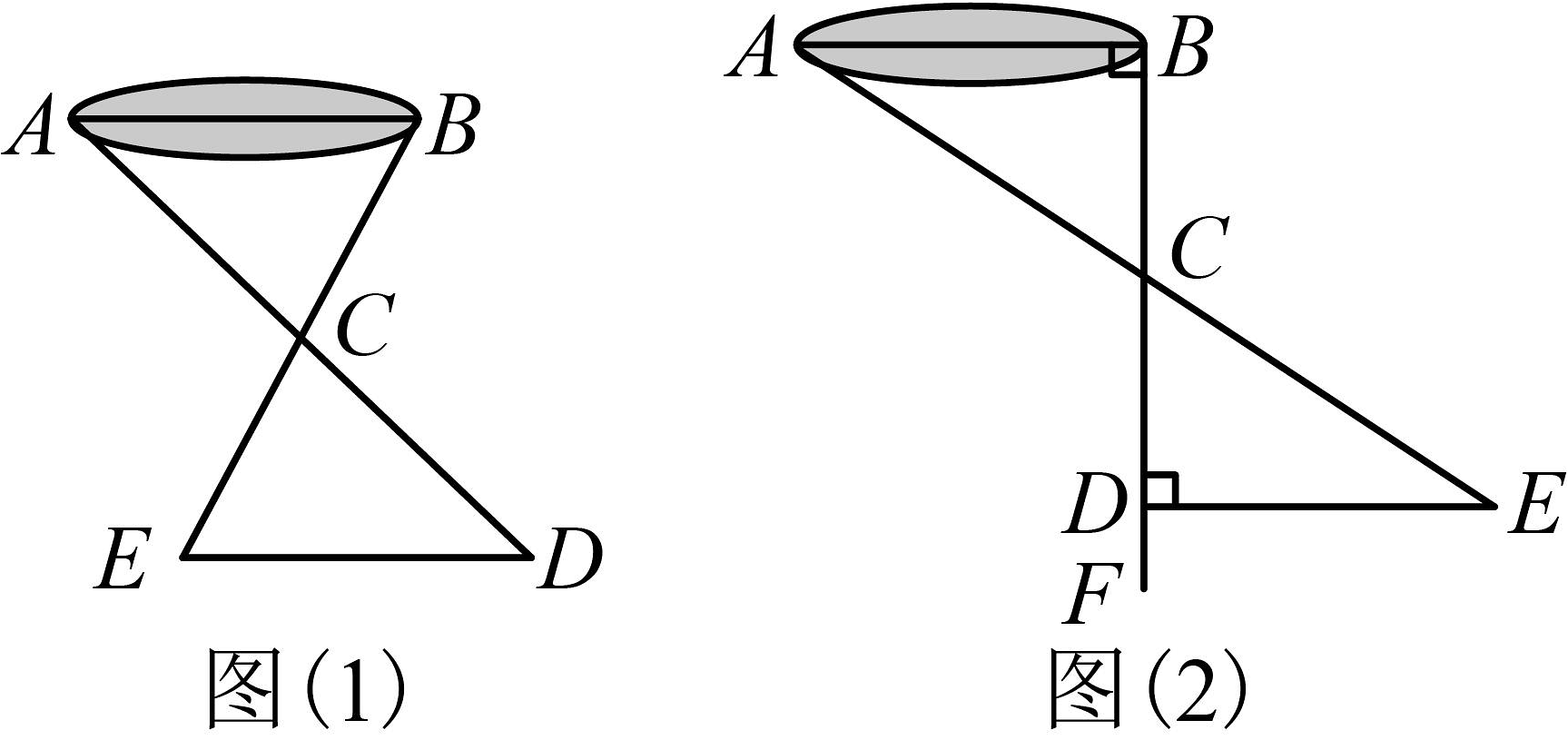
【问题情境】如图所示，池塘的两端有A，B两点，现需要测量该池塘的两端A，B之间的距离，需要如何进行呢？
【提出方案】同学们想出了如下的两种方案：
甲同学：如图（1）所示，先在平地上取一个可直接到达A，B的点C，再连接 $A C ， B C$ ，并分别延长 $A C$ 至点D， $B C$ 至点E，使 $D C = A C$ ， $E C = B C$ ，最后量出 $D E$ 的距离就是 $A B$ 的距离；
乙同学：如图（2）所示，过点B作 $A B$ 的垂线 $B F$ ，在 $B F$ 上取C，D两点，使 $B C = C D$ ，接着过点D作 $B D$ 的垂线 $D E$ ，在垂线上选一点E，使A，C，E三点在一条直线上，则测出 $D E$ 的长即是 $A B$ 的距离．
【问题解决】请你选择一位同学的方案，判断其是否可行，并说明理由．

查看解析
15、如图，在△ABC中．

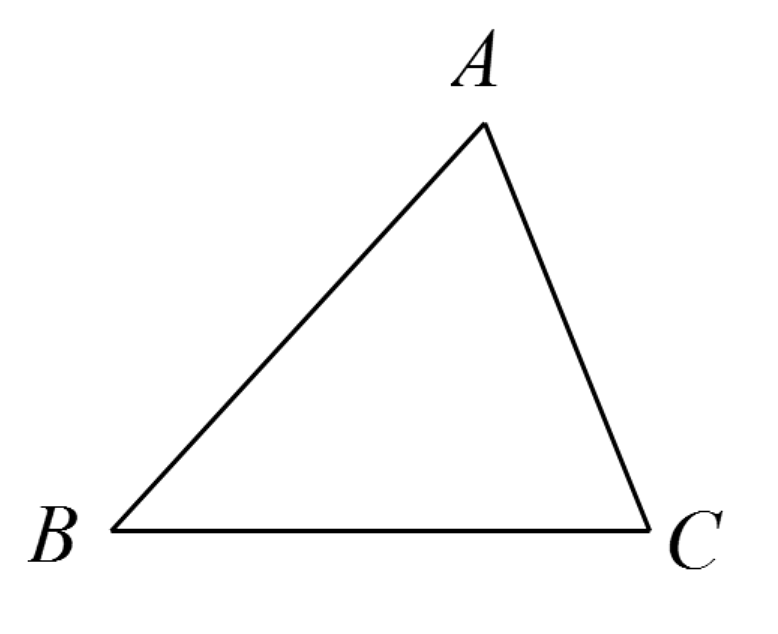(1)、作△ABC的中线CD．（尺规作图，不写作法，保留作图痕迹）

(2)、若 $C D = A D$ ，求 $∠ A C B$ 的度数．

查看解析
16、如图所示，在平面直角坐标系中， $A_{} (1, 2), B_{} (3, 1), C_{} (- 2, - 1)$ ．

(1)、在图中作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出 $A_{1}, B_{1}, C_{1}$ 的坐标；

(2)、求 $△ A_{1} B_{1} C_{1}$ 的面积；

(3)、在x轴上求作一点P，使 $P A + P B$ 的值最小（保留作图痕迹，不写作法）

查看解析
17、如图，在 $△ A B C$ 中， $∠ A B C = 60 °$ ， $B E$ 平分 $∠ A B C$ ， $A D$ 为 $B C$ 边上的高，若 $∠ B E C = 75 °$ ，求 $∠ D A C$ 的度数．

查看解析
18、某校用红色灯带制作了一个如图所示的正五角星（ $A 、 B 、 C 、 D 、 E$ 是正五角的五个顶点），则图中 $∠ A$ 的度数是度．

查看解析
19、点 $P (- 2, 4)$ 关于x轴的对称点的坐标是．

查看解析
20、一个多边形的每一个内角都是 $108 °$ ，则它的边数为．

查看解析

上一页 1133 1134 1135 1136 1137 下一页跳转

星期三	$+ 8$
星期四	■
星期五	$- 14$
三天合计	$+ 3$