-
1、某城市12个月平均最高气温t(℃)与月份的函数关系如图。
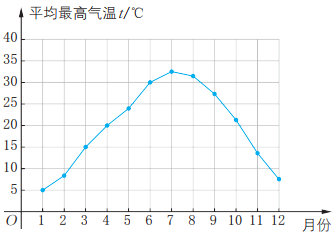(1)、求该城市1月，7月的平均最高气温。(2)、分析该城市1月到12月的气温变化情况，并说明哪个月最冷、哪个月最热。 -
2、 如图，设正方形的面积为y(cm2)，边长为x(cm)。
(1)、求y关于x的函数表达式，并求自变量x的取值范围。(2)、 分别求当x=5，10时，函数y的值。 -
3、专家建议，每人每天的食盐摄入量以不超过5g为宜。为控制食盐摄入，某单位向员工发放一个小盐勺(容量为1g)。设家庭人数为x，家庭每天应摄入食盐勺数的最大值为y。(1)、写出y与x的函数关系式和自变量x的取值范围。(2)、当x=3时，y的值是多少?说明此时函数值的实际意义。
-
4、一列行驶中的火车的速度为每小时160千米，用t(时)表示行驶的时间，s(千米)表示行驶的路程。其中常量是 ， 变量是 ， s关于t的函数表达式是。当t=2.5时，函数s的值是 ， 它的实际意义是。
-
5、检验游泳池的水质时，要求三次检验的水的pH的平均值不小于7.2，且不大于7.8。前两次检验，水的pH分别是7.4，7.9，那么第三次检验的水的pH应该为多少才能合格?
-
6、解下列一元一次不等式组：(1)、(2)、
-
7、若不等式组 的解集为x≥-b，则下列各式正确的是( )。A、a>b B、a<b C、b≤a D、a≤b
-
8、解下列一元一次不等式组：(1)、(2)、(3)、(4)、
-
9、利用数轴，分别求出满足下列各组不等式的x值的公共部分。(1)、(2)、(3)、(4)、
-
10、解由两个一元一次不等式组成的不等式组，在取各个不等式的解集的公共部分时，有几种不同情况?
若 ， 你能说出下列四种情况下不等式组的解集吗?借助数轴来寻找结果。
(1)、(2)、(3)、(4)、(请与你的同伴交流)
-
11、一个长方形足球训练场的长为 x（m），宽为 70 m。 如果它的周长大于 350 m，面积小于7560 m2 ， 你能确定 x 的取值范围吗？判断这个足球训练场的尺寸是否符合国际足球比赛的要求(注：用于国际比赛的足球场的长在100m到110m之间，宽在64m到75m之间)。
-
12、解下列一元一次不等式组，并把解集在数轴上表示出来。(1)、(2)、
-
13、利用数轴，求出满足下列各组不等式的x值的公共部分。(1)、(2)、(3)、(4)、
-
14、解一元一次不等式组
-
15、解一元一次不等式组
-
16、下图是某水库的库容曲线图，其中x表示水库的平均水深(米)，V表示水库的库容(万立方米)。根据图象回答下面的问题。
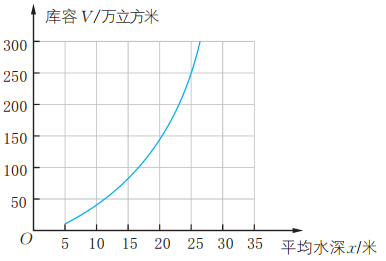(1)、这个函数反映了哪两个变量之间的关系?(2)、 填表：x/米
5
10
15
20
25
V/万立方米
(3)、当平均水深取5m至25m之间的一个确定的值时，相应的库容V确定吗?(4)、库容V可以看成平均水深x的函数吗?(5)、求当x=18时的函数值，并说明它的实际意义。 -
17、某小区临时停车收费规则如下：半小时内(含半小时)收费5元；超过半小时，每小时收费10元(不足1小时按1小时计)；每天不超过40元。如果停车时间为x(h)，停车费为y(元)。(1)、y是关于x的函数吗?为什么?(2)、分别求当x=0.5，1，3.4，6时的函数值，并说明它们的实际意义。
-
18、已知△ABC的底边BC上的高线长是6cm。当BC的长改变时，三角形的面积也将改变。(1)、 若△ABC的底边BC的长为x(cm)，则△ABC的面积y(cm2)可表示为。(2)、当底边BC的长x从12cm变化到3cm时，三角形的面积y从cm2变化到cm2。
-
19、求下列函数当x=4时的函数值。(1)、(2)、
-
20、某市民用电费的价格是0.538元/千瓦时。设用电量为x千瓦时，应付电费为y元，则y关于x的函数表达式是。当x=40时，函数值是 ， 它的实际意义是。若某用户的用电量为65千瓦时，则该用户应付电费为元。