-
1、一次招聘会上，A，B两公司都在招聘销售人员。A公司给出的工资待遇是：每月3280元基本工资，另加销售额的2%作为奖金；B公司给出的工资待遇是：每月2840元基本工资，另加销售额的4%作为奖金。如果你去应聘，那么你将怎样选择?
-
2、利用一次函数图象，求二元一次方程组 的解。
-
3、如图，在直角坐标系中，O是原点，已知梯形ABCD的顶点A，B，D的坐标分别为A(-3，0)，B(-1，- )，D(0，2)，AB∥CD，BC经过点O。
(1)、 求证：BO=CO。(2)、 求梯形ABCD的面积。 -
4、小聪和小慧去某风景区游览，约好在飞瀑见面。上午7：00，小聪乘电动汽车从古刹出发，沿景区公路(图)去飞瀑，车速为30km/h。小慧于上午7：00从塔林出发，骑电动自行车沿景区公路去飞瀑，车速为20km/h。
(1)、当小聪追上小慧时，他们是否已经过了草甸?(2)、当小聪到达飞瀑时，小慧离飞瀑还有多少千米? -
5、 如图，已知AD⊥BD，AC⊥BC，E为AB的中点。试判断DE与CE是否相等，并给出证明。
-
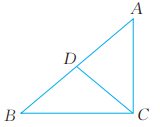
6、 如图，在Rt△ABC中，CD是斜边AB上的中线，∠CDA=80°。求∠A，∠B的度数。
-
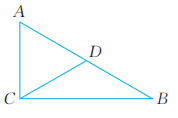
7、 如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB=1.5。D为斜边AB的中点，连结CD。求AC，CD的长。
-
8、 已知：如图，△ABC是等腰三角形，AC⊥BC，CD⊥AB。
(1)、 求∠A，∠B的度数。(2)、 求证：AD=CD=BD。 -
9、用一副三角尺拼出甲、乙两个图形，求：
(1)、 图甲中，∠ABD的度数。(2)、 图乙中，∠DCF，∠CFD，∠AEF的度数。 -
10、 在△ABC中，∠A=90°，∠B=3∠C。求∠B，∠C的度数。
-
11、 已知在Rt△ABC中，斜边上的中线CD=5cm，求斜边AB的长。
-
12、 如图，在Rt△ABC中，AC⊥BC，CD⊥AB。找出所有互余的角。
-
13、如图，一名滑雪运动员沿着倾斜角为30°的斜坡，从A滑行至B，已知AB=200m。问：这名滑雪运动员的高度下降了多少米?
-
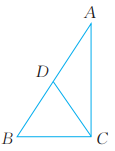
14、 已知：如图，D是Rt△ABC斜边AB上的一点， CD。求证：AD=CD。
-
15、已知直角三角形两个锐角的度数之比为3：2，求这两个锐角的度数。
-
16、如图，每个图形都是由若干枚棋子围成的正方形图案，图案的每条边(包括两个顶点)上都有 枚棋子，设每个图案的棋子总数为S。
图中，棋子的排列有什么规律?S与n之间能用函数表达式表示吗?自变量n的取值范围是什么?
-
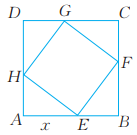
17、如图，正方形EFGH的四个顶点分别在边长为1的正方形ABCD的四条边上。设. 试求正方形EFGH的面积y关于x的函数表达式，写出自变量x的取值范围，并求当 时，正方形EFGH的面积。
-
18、游泳池应定期换水。某游泳池在一次换水前存水936立方米，换水时打开排水孔，以每小时312立方米的速度将水放出。设放水时间为t小时，游泳池内的存水量为Q立方米。
(1)、求Q关于t的函数表达式和自变量t的取值范围。(2)、放水2小时20分后，游泳池内还剩多少立方米的水?(3)、放完游泳池内全部水需要多少时间? -
19、观察下列整式的次数和项数，找出它们的共同特征，给以名称，并作出定义。
-
20、把下列命题改写成“如果……那么……”的形式。(1)、同角的余角相等；(2)、同号两数相乘，积为正数。