-
1、小军和小红分别以直角梯形的上底和下底所在的直线为轴，将梯形旋转一周，得到了两个立体图形．
小军：我们旋转的平面图形是完全一样的，所以旋转后得到的两个立体图形的体积相等．
小红：我不同意你的看法，我认为甲、乙两个立体图形的体积不相等．
(1)、你同意的说法．(2)、甲、乙两个立体图形的体积比是多少？ -
2、计算：(1)、(2)、
-
3、下列式子中，正确的是（ ）A、 B、 C、 D、
-
4、如图，BD是长方形ABCD的一条对角线。
(1)、 △ABD与△CDB全等吗? 你是怎样知道的?(2)、 如果你认为△ABD与△CDB全等，请用符号表示，并说出它们的对应边和对应角。 -
5、 如图，在△ABC中，AD⊥BC于点D，BD=CD。完成下面说明∠B=∠C的理由的过程(填空)。
解：由AD⊥BC(已知)，
得∠ADB==Rt∠(垂直的定义)。
当把图形沿AD对折时，射线DB与DC。
由BD=CD ()，
可知点B与点重合，
所以△ABD与△ACD ，
即△ABD△ACD(全等三角形的定义)，
所以∠B=∠C ()。
-
6、判断下列说法是否正确，并简要说明理由。(1)、长和宽分别相等的长方形都是全等图形；(2)、如图所示两幅剪纸图案全等；
(3)、面积相等的两个三角形是全等三角形。 -
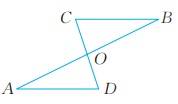
7、 如图，△OAD与△OBC全等，∠A与∠B是对应角。请用符号表示这两个三角形全等，并写出相等的边和角。
-
8、如图，已知△AOC≌△DOB。说出它们的对应边和对应角。
-
9、半径相等的两个圆是全等图形吗?你是怎样知道的?
-
10、如图，AD平分∠BAC，AB=AC。△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?先判断，再说明理由。
-
11、如图，△AOC与△BOD全等。用符号“≌”表示这两个三角形全等。已知∠A与∠B是对应角，写出其余的对应角和各对对应边。
-
12、如图，画在透明纸上的△ABC和△A'B'C'是全等图形吗?你是怎么判断的?
-
13、下面各对图形是不是全等图形?为什么?
(1)、边长都是10cm的两个正方形；(2)、如图所示的两件衣服。 -
14、已知：如图，点A，C，F，D在同一条直线上，且. AF=DC。求证：BC∥EF。
-
15、 如图，在四边形ABCD中， 。请通过添加辅助线，把它分成两个全等三角形，并给出证明。
-
16、 如图，已知AB=AC，BD=CD。求证：∠1=∠2。
-
17、 如图，已知∠α。用直尺和圆规作∠ABC，使∠ABC=∠α。
-
18、 已知：如图，在△ABC中，AB=AC，AD是BC边上的中线。求证：AD⊥BC(填空)。
证明：在△ABD和△ACD中，
因为
所以≌()。
故∠ADB=(全等三角形的对应角相等)，
进而有 (平角的定义)，
所以AD⊥BC(垂直的定义)。
-
19、 如图，点B，E，C，F在同一条直线上，且AB=DE，AC=DF，BE=CF。将下面证明△ABC≌△DEF的过程补充完整。
证明：因为BE=CF( )，
所以BE+EC=CF+EC，即BC=EF。
在△ABC和△DEF中，
因为所以△ABC≌△DEF( )。
-
20、举出两个应用三角形稳定性的实际例子。