-
1、已知:如图,点 , 在线段上, , , .
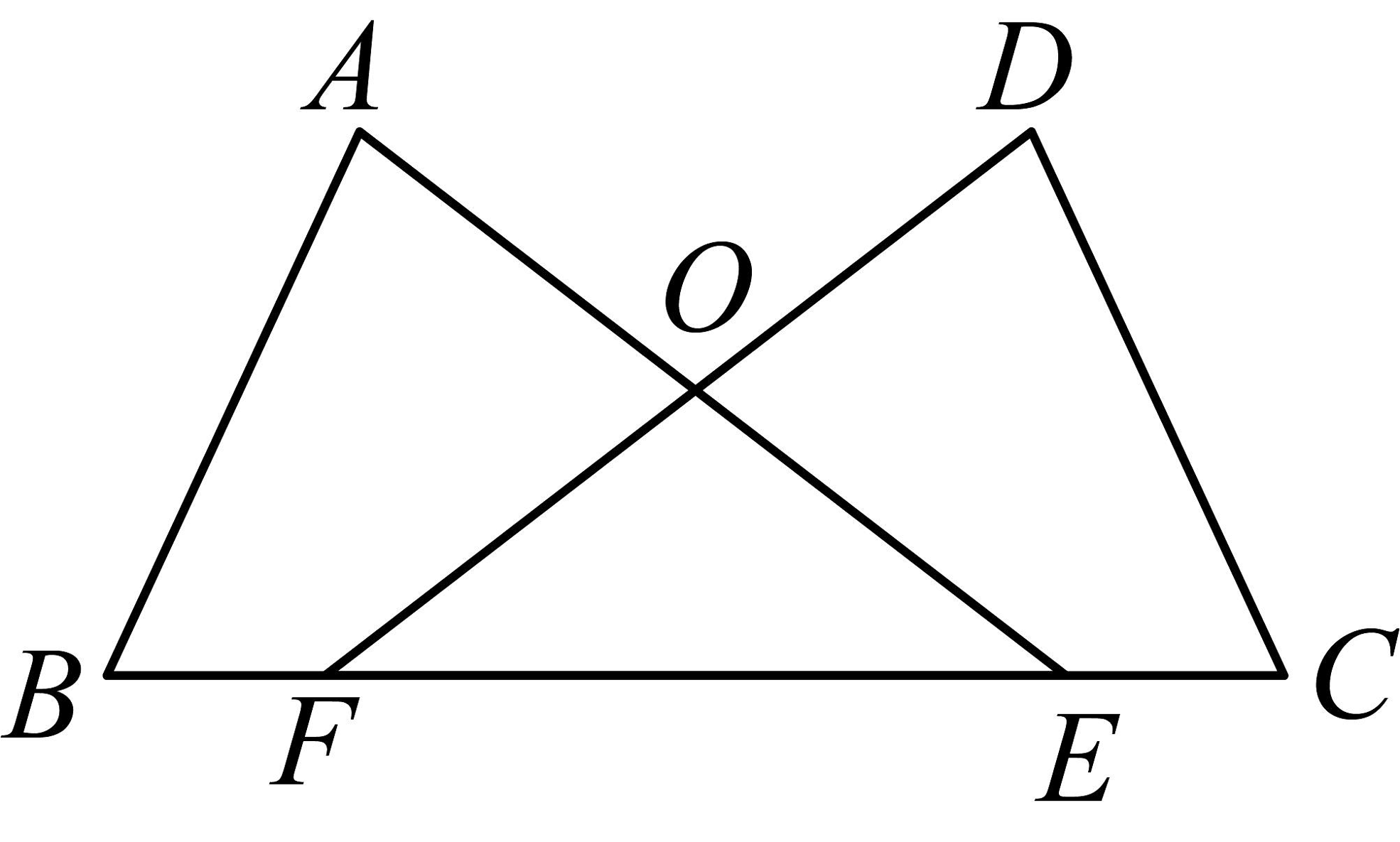 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数. -
2、解下列不等式,并把解表示在数轴上.(1)、;
 (2)、 .
(2)、 .
-
3、如图,等边三角形ABC的边长为6,点是的中心, , 绕点旋转 , 分别交线段AB、BC于D、E两点,连接DE,则周长的最小值为 .
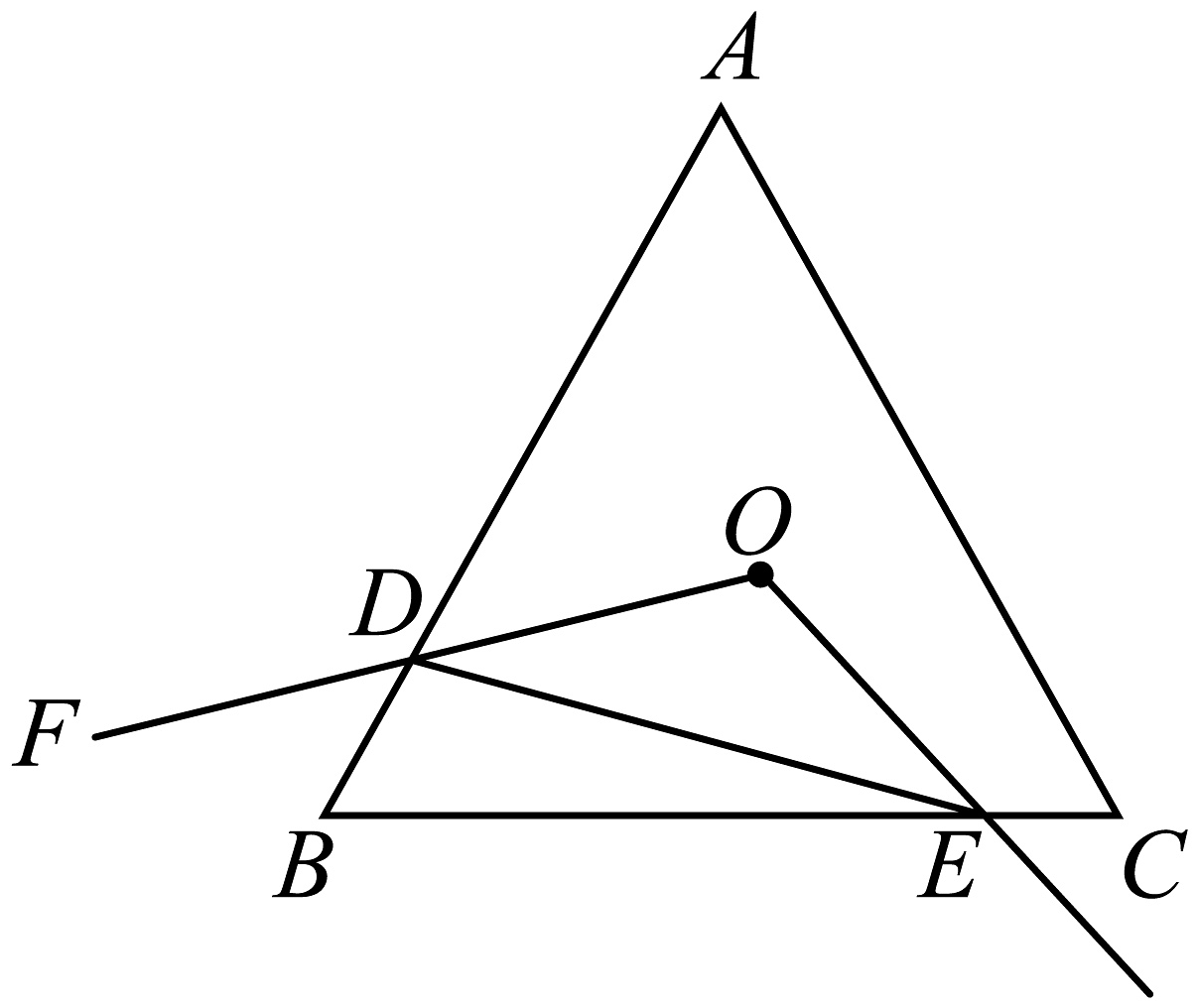
-
4、如图,在中, , 由图中的尺规作图得到射线 , 与交于点E,点F为的中点,连接 , 若 , 则的长为 .

-
5、如图,在中,是的高,分别以线段为边向外作正方形,其中3个正方形的面积如图所示,则第四个正方形的面积为 .
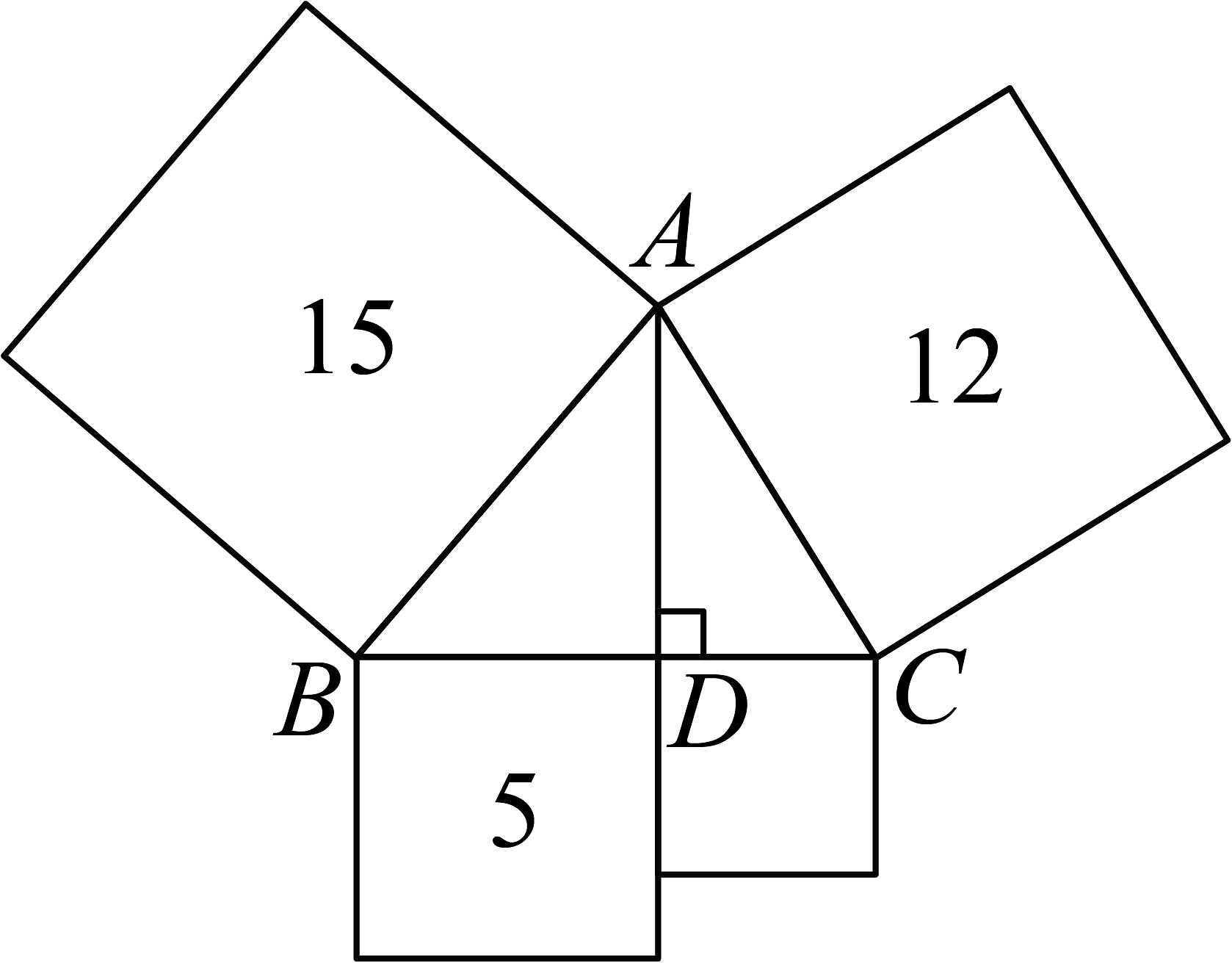
-
6、如图,已知 , A与D,C与E分别是对应顶点,点E在线段上, , , 则的长为 .
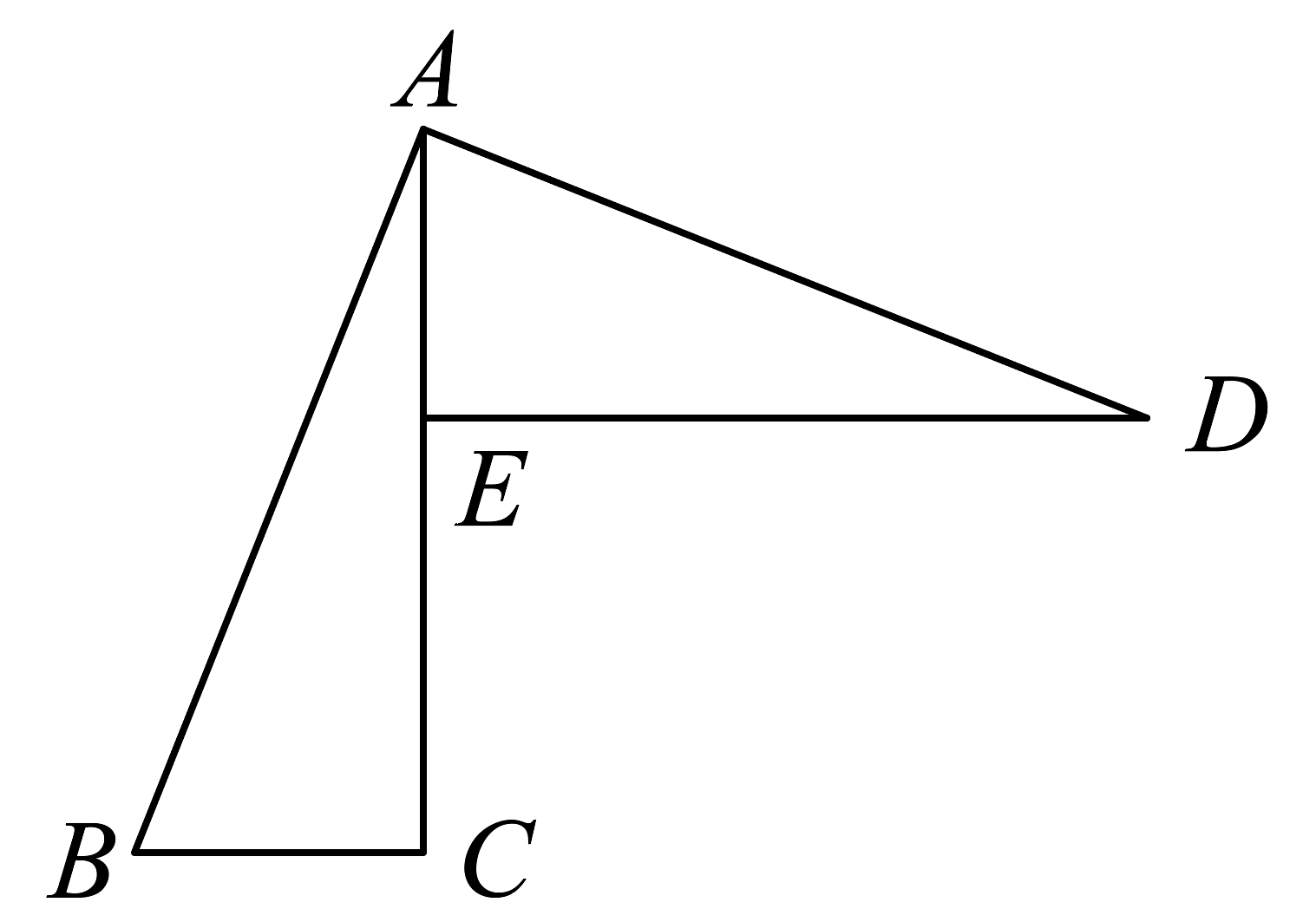
-
7、命题“如果 , 那么 . ”的逆命题为 .
-
8、如图,在中, , , 是的角平分线,E,F分别在 , 边上. , , 连结 , . 若 , 则的面积是( )
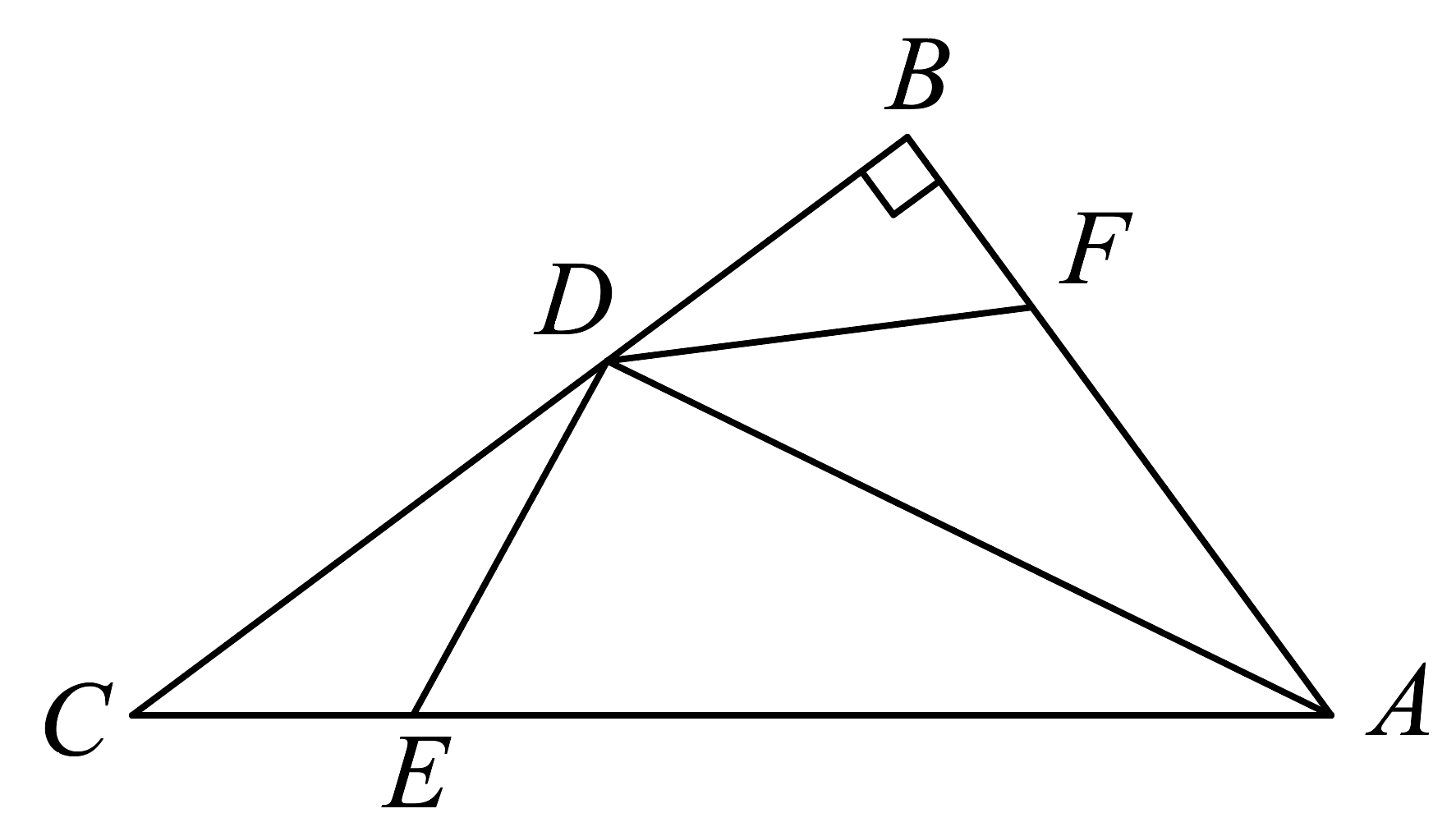 A、 B、24 C、30 D、
A、 B、24 C、30 D、 -
9、如图,在中,分别以点 , 为圆心,大于的长为半径作弧,两弧分别交于点 , , 直线分别交与于点和 , 连结 , 若 , 的周长为 , 则的周长是( )
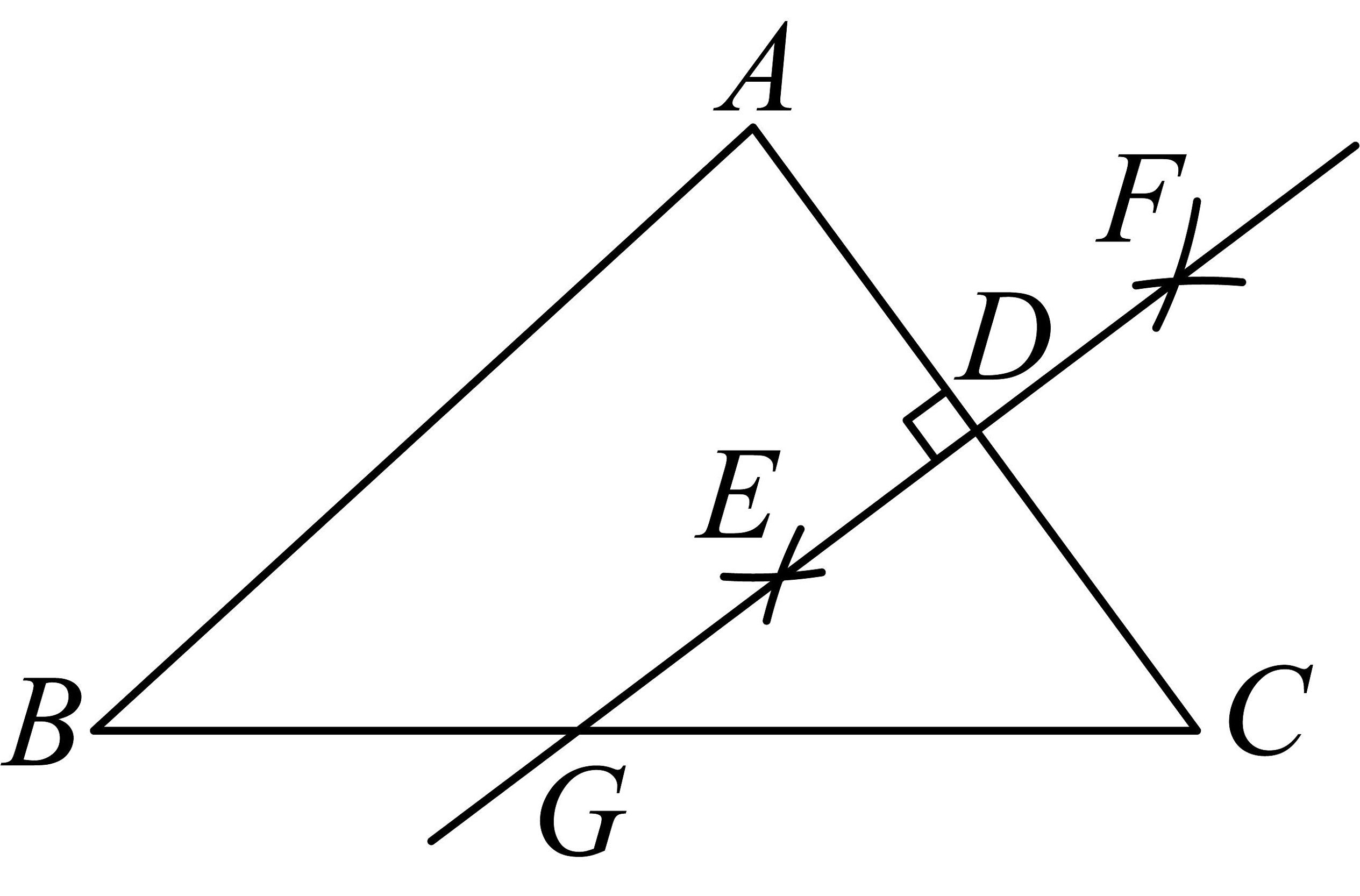 A、 B、 C、 D、
A、 B、 C、 D、 -
10、如图,在中, , 是斜边上的中线,若 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,在中,的平分线交于点D, , 若 , 则线段的长度是( )
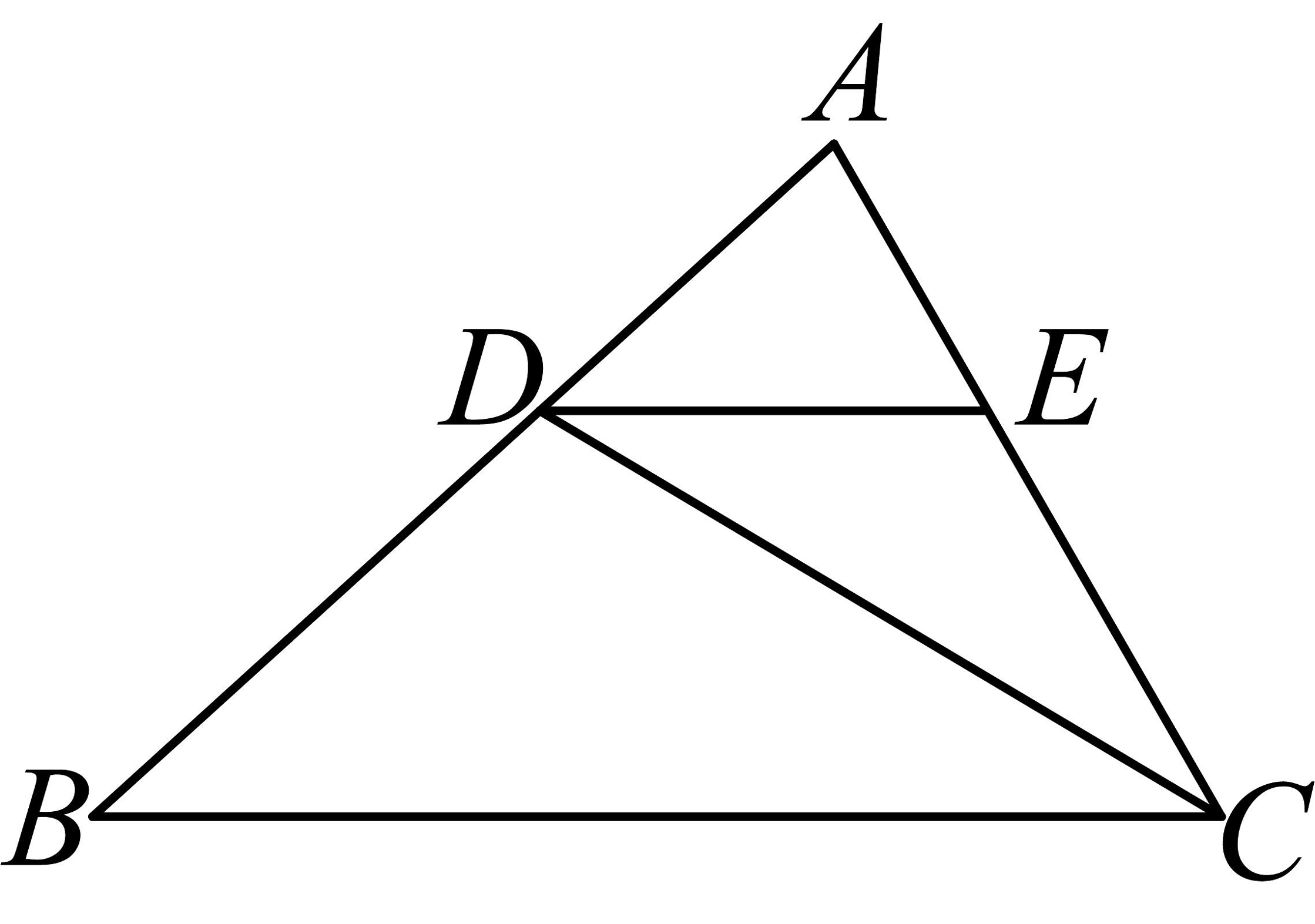 A、4 B、8 C、12 D、16
A、4 B、8 C、12 D、16 -
12、在中, , 则的度数是( )A、 B、 C、 D、
-
13、若三角形两边长分别是5和8,则第三边长可能是( )A、1 B、3 C、8 D、13
-
14、对于命题“如果 , 那么 . ”能够说明它是假命题的反例是( )A、 B、 C、 D、
-
15、下面的交通标志中,轴对称图形是( ).A、
 B、
B、 C、
C、 D、
D、
-
16、定义:在平面直角坐标系中,将直线中a和b的值都扩大到原来的倍,得到新的直线 , 则称直线为直线的“k倍伴随线”,例如直线的“2倍伴随线”的函数解析式为 .(1)、求直线的“3倍伴随线”的函数表达式;(2)、若点在直线的“2倍伴随线”上,求m的值.
-
17、若点在y轴上,则点在第象限.
-
18、如图1, , 点A、B分别在上运动(不与点O重合).
 (1)、若是的平分线,的反方向延长线与的平分线交于点D.
(1)、若是的平分线,的反方向延长线与的平分线交于点D.①若 , 则__________ .
②猜想:的度数是否随点A、B的移动发生变化,并说明理由.
(2)、如图2,若将“”改为“()”,, 其余条件不变,__________(直接用含、n的代数式表示的度数).
-
19、(1)完成下面的推理说明:
已知:如图, , 、分别平分和 .
求证: .

证明:、分别平分和(已 知) ,
, ( ).
( ),
( ).
( ).
(等式的性质) .
( ).
(2)说出(1)的推理中运用了哪两个互逆的真命题 .
-
20、如图,在中.是边上的高,平分求的度数.
