-
1、根据下列所给条件,不能列出方程的是( ).A、某数比它的平方小 B、某数加上 , 再乘等于 C、某数与它的的差 D、某数的倍与的和等于
-
2、在数轴上,表示数a的点与原点的距离叫做数a的绝对值,记作 , 则2024的绝对值是( )A、 B、2024 C、 D、
-
3、“一盔一带”是公安部在全国开展的一项安全守护行动,也是营造文明城市,做文明市民的重要标准,“一盔”是指安全头盔,电动自行车驾驶人和乘坐人员应当佩戴安全头盔.某商场欲购进一批安全头盔,已知购进3个甲种型号头盔和2个乙种型号头盔需要220元,购进1个甲种型号头盔和5个乙种型号头盔需要290元.
 (1)、甲、乙两种型号头盔的进货单价分别是多少?(2)、若该商场计划购进甲、乙两种型号头盔共200个,且乙种型号头盔的购进数量最多为90个.已知甲种型号头盔每个售价为55元,乙种型号头盔每个售价为75元.若该商场将这两种型号头盔全部售出可获利W元,则应该如何进货才能使该商场获利最大?最大利润是多少元?
(1)、甲、乙两种型号头盔的进货单价分别是多少?(2)、若该商场计划购进甲、乙两种型号头盔共200个,且乙种型号头盔的购进数量最多为90个.已知甲种型号头盔每个售价为55元,乙种型号头盔每个售价为75元.若该商场将这两种型号头盔全部售出可获利W元,则应该如何进货才能使该商场获利最大?最大利润是多少元? -
4、【问题背景】小李同学在学习了数学第13章内容后,他对三角形的三边关系及三角形的中线特别感兴趣,下面是他总结的一些题目笔记.请同学们帮他分析.
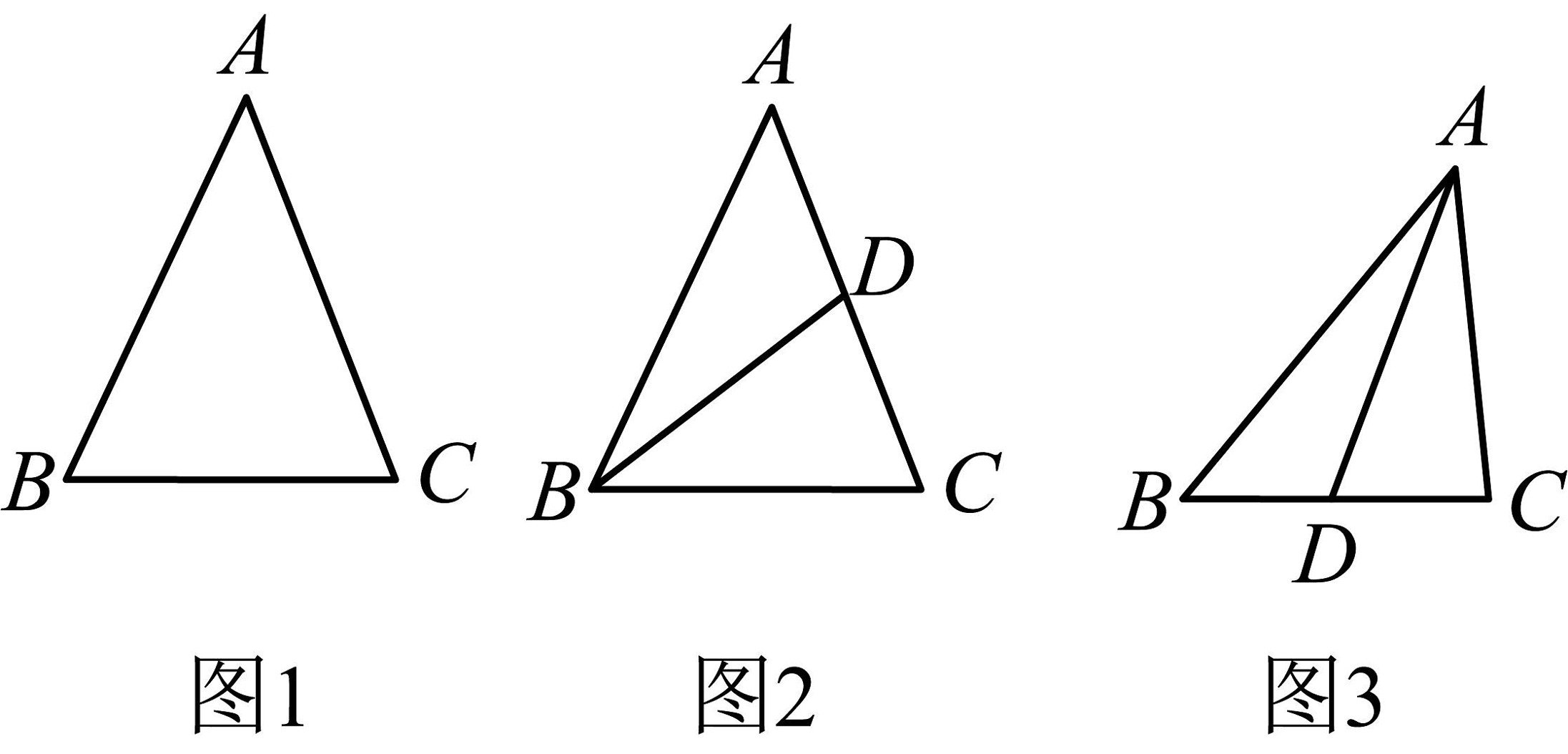
【新知探究】如图1,在等腰中,、是的腰.已知三角形两条边的长度分别为 , , 求的周长?小李经过计算,得出的的周长是或 .
任务1:小李的答案是否正确?如果不正确请写出正确的答案.
【新知拓展】根据【任务1】的答案,小李继续探索三角形中线的重要作用.
如图2,当添加条件:是等腰的中线时.求与的周长差.
任务2:请你帮小李写出解答过程.
【拓展应用】结合【任务2】的解答过程,小李继续探索三角形中线在一般三角形中是否具有同样作用.
如图3,在中,已知是的中线(且),其中 , . 则与的周长差是多少.
任务3:请用含 , 的代数式表示与的周长差.
-
5、如图,在平面直角坐标系中直线m:与直线n:交于点 , 直线m、n分别与x轴交于点B、C,其中点 .
 (1)、求直线m对应的函数表达式;(2)、求的面积;(3)、直接写出不等式的解集.
(1)、求直线m对应的函数表达式;(2)、求的面积;(3)、直接写出不等式的解集. -
6、如图,在中, , , 是的角平分线,是的角平分线.求的度数.

-
7、已知点 , 解答下列各题.(1)、点P在x轴上,求点P的坐标;(2)、点Q的坐标为 , 直线轴,求点P的坐标.
-
8、观察以下图形,猜测第个图形中有个三角形(用含的代数式表示结论)

-
9、等腰三角形有一个角的度数为 , 则它一条腰上的高与另一条腰的夹角的度数是 .
-
10、直线经过点 , 则的值为 .
-
11、若点和点在一次函数的图象上,则(用“>”、“<”或“=”连接).
-
12、给出下列4个命题:
①垂线段最短;②两条直线被第三条直线所截,内错角相等;
③互补的角是邻补角;④同旁内角相等,两直线平行.
其中是真命题的是 . (填写命题的序号即可)
-
13、函数自变量的取值范围是 .
-
14、在平面直角坐标系中,线段是由线段经过平移得到的,已知点的对应点为 , 点B的对应点的坐标为 , 则点B的坐标为( )A、 B、 C、 D、
-
15、象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点的位置,则在同一坐标系下,“马”所在位置是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、阅读材料:如图,某校的“图书码”共有7位数字,它是由6位数字代码和校验码构成,其结构分别代表“种类代码、出版社代码、书序代码和校验码”.其中,校验码是用来校验图书码中前6位数字代码的正确性.它的编制是按照特定的算法得来的.以此图为例,其算法为:

步骤1:计算前6位数字中偶数位数字的和a,即;
步骤2:计算前6位数字中奇数位数字的和b,即;
步骤3:计算与b的和c,即;
步骤4:取大于或等于c且为的整数倍的最小数d,即;
步骤5:计算d与c的差就是校验码X,即 .
请解答下列问题:
(1)、《数学故事》的图书码为 , 请分别计算步骤3中c的值和校验码Y的值;(2)、如图①,某图书码中的一位数字被墨水污染了,设这位数字为m,求m;(3)、如图②,某图书码中被墨水污染的两个数字的和是8,这两个数字从左到右分别是多少? -
17、如图1,是等边内一点,连结 . 将线段绕点顺时针旋转得到线段 , 连结 .
 (1)、求证: .(2)、如图2,连结 .
(1)、求证: .(2)、如图2,连结 .①当 , 且为等腰三角形时,求出的度数.
②当 , 且时,请直接写出点到点的距离.
-
18、如图,在四边形中, , 连接 , 点E在线段上,连接 , , .
 (1)、求证: .(2)、若 , .
(1)、求证: .(2)、若 , .①求的度数.
②当 , 时,求的面积.
-
19、近期,国风矿物质颜料在网络上大火,引得各绘画爱好者争先购买.其中“岩灰”和“石绿”风靡一时,1瓶“岩灰”和1瓶“石绿”总价100元,“石绿”比“岩灰”单价高40元.(1)、分别求出“岩灰”和“石绿”的销售单价;(2)、某同学欲购买两种颜料共10瓶,预算资金不超过400元,则该同学最多可以购买多少瓶“石绿”?
-
20、
尺规作图问题
问题呈现
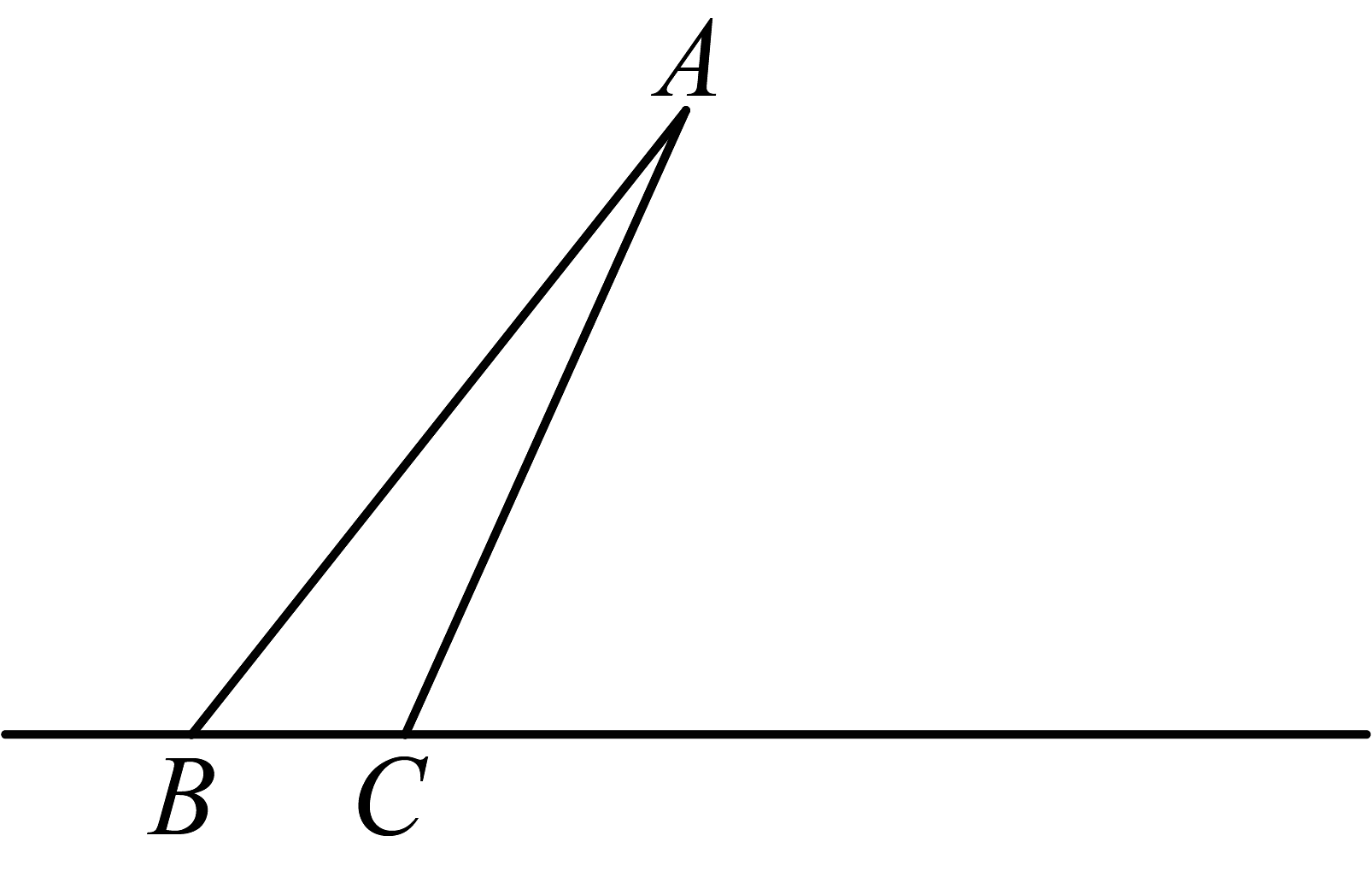
如图,已知直线和直线外一点 , 连接 , .
(1)用无刻度的直尺和圆规在直线上取点 , 点(点在点的左侧),使得 , 且(不要求写作法,但要保留作图痕迹);
(2)请根据自己的作法说明作图正确的理由.
我的画法
我的理由