-
1、在▱ABCD中,BE⊥AC于点E , DF⊥AC于点F .
求证:AF=CE .

-
2、计算: .
-
3、如图,在矩形ABCD中,对角线AC、BD相交于点O , AE⊥BD于E , 若BE=OE , AB=2,则BC的长为 .

-
4、如图,平行四边形ABCD的对角线AC , BD交于点E , F是DC的中点,若EF=2,则BC= .

-
5、如图,已知直线y1=2x+3与直线y2=kx+b(k≠0)交于点(n , 6),则关于x的不等式kx+b≥2x+3的解集为 .

-
6、某校为调查学生对2023年播出的《感动中国》节目中英雄人物事迹的了解情况,选取甲、乙、丙三个班级进行“感动中国故事知多少”的问卷测试,若甲、乙、丙三个班级的平均分相同,且方差分别为S甲2=5.48,S乙2=5.32,S丙2=5.17,则甲、乙、丙三个班级中成比较稳定的是 班.(填“甲”或“乙”或“丙”)
-
7、代数式在实数范围内有意义时,x应满足的条件是 .
-
8、如图,在菱形ABCD中,对角线AC , BD相交于点O , 点E是AD的中点,连接OE , 若AC=6,BD=8,则下列结论错误的是( )
 A、AB=5 B、 C、菱形的面积为48 D、点A到BC的距离为
A、AB=5 B、 C、菱形的面积为48 D、点A到BC的距离为 -
9、对于一次函数y=2x﹣1,下列结论不正确的是( )A、它的图象与y轴交于点(0,﹣1) B、y随x的增大而增大 C、当时,y>0 D、它的图象经过第一、二、三象限
-
10、若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y2>y1>y3 C、y1>y3>y2 D、y3>y2>y1
-
11、下列计算正确的是( )A、 B、 C、 D、
-
12、下列函数中,y是x的正比例函数的是( )A、y=x﹣1 B、 C、y=2x2 D、y=3x
-
13、若添加一个条件,使得▱ABCD是菱形,则这个条件可以是( )A、AB=CD B、AC=BD C、AC⊥BD D、AB⊥BC
-
14、某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手
评分(满分100)
Deep Seek
88
豆包
84
腾讯元宝
84
夸克
86
评分的众数和中位数分别是( )
A、84,86 B、84,88 C、88,85 D、84,85 -
15、如图,已知∠1+∠2=180°,且∠3=∠B.
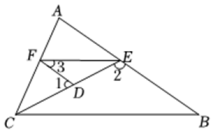 (1)、试判断EF和BC的位置关系,并说明理由;(2)、若CE平分∠ACB,且∠2=108°,∠3=52°,求∠AFE的度数.
(1)、试判断EF和BC的位置关系,并说明理由;(2)、若CE平分∠ACB,且∠2=108°,∠3=52°,求∠AFE的度数. -
16、已知如图,在△ABC中,三个顶点的坐标分别为A(2,3),B(5,-2),C(1,1),将△ABC沿x轴负方向平移4个单位长度,再沿y轴负方向平移2个单位长度,得到△DEF,其中点A的对应点为点D,点B的对应点为点E,点C的对应点为点F.
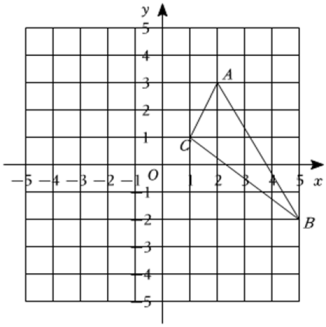 (1)、直接写出平移后的△DEF的顶点坐标;(2)、在坐标系中画出平移后的△DEF;(3)、求出△DEF的面积.
(1)、直接写出平移后的△DEF的顶点坐标;(2)、在坐标系中画出平移后的△DEF;(3)、求出△DEF的面积. -
17、在平面直角坐标系中,有一点P(2x-1,3x).(1)、若点P在x轴上,求x的值;(2)、若Q(5,8),且PQ∥y轴,求出点P的坐标;(3)、若点P在第一象限,且到两坐标轴的距离之和为9,求点P的坐标.
-
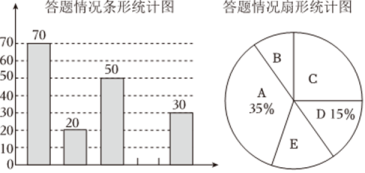
18、随着科技的进步,越来越多的学习软件进入我们的生活,帮助学生学习知识.某校对学生最喜爱的学习辅助软件进行了抽样问卷调查,调查问卷和统计结果描述如下:
“你最喜爱的学习辅助软件”调查问卷
问题:在以下五个软件中,你最喜爱的是ㅤㅤㅤ .
(A)作业帮
(B)橙果错题集
(C)小猿搜题
(D)豆包
(E)DeepSeek
根据以上信息,解答下列问题:
(1)、求本次调查中最喜爱豆包软件的学生人数,并补全条形统计图.(2)、已知该校有学生1500人,根据统计信息,估算该校最喜爱DeepSeek软件的学生人数. -
19、为了响应节能减排的号召,推动绿色生活方式,某汽车4S店准备购进A型和B型两种不同型号的电动汽车.经市场调查发现,如果购进2辆A型车和1辆B型车,需要66万元;如果购进3辆A型车和2辆B型车,需要114万元.(1)、求A型、B型电动汽车的单价;(用二元一次方程组解决问题)(2)、该4S店最终决定本月购进这两种电动汽车共20辆,但是总费用不超过500万元,那么该4S店最少需要购进A型电动汽车多少辆?(用一元一次不等式解决问题)
-
20、(1)、计算: + -|-2|-(2)、解方程:(2x-1)2-16=9.