-
1、在某校科技文化节系列活动中，举办了“魅力几何，勾勒未来”的竞赛活动，A班和B班各有10名学生参加该竞赛活动.统计两个班的竞赛成绩（满分100），并对数据（成绩）讲行了收集、分析如下.
【收集数据】
A班10名学生竞赛成绩：18，40，60，80，60，80，92，80，70，100
B班10名学生竞赛成绩：24，90，40，88，68，86，68，72，74，70
【分析数据】
班级
平均数
中位数
众数
A班
68
b
80
B班
a
71
c
【解决问题】根据以上信息，回答下列问题：
(1)、请你分别求出a，b，c的值.(2)、请你根据【分析数据】中的信息，判断哪个班成绩比较好，并简要说明理由. -
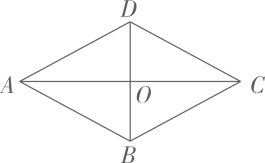
2、如图，□ABCD的对角线AC，BD相交于点O，且AC=4，BD=2，BC= ， 求证；□ABCD是菱形.
-
3、人体正常体温在36.5℃左右，但是在一天中的不同时刻，体温也不尽相同，如图反映了小香在一天24小时中，其体温与时间之间的对应关系，
(1)、对应关系中的自变量是什么？(2)、小香体温最高和最低的分别是多少℃？(3)、小香体温由高到低变化的是哪些时段？ -
4、计算：.
-
5、如图，在□ABCD中，AB=4，BC=6，点E为直线BC上一动点，连接AE，DE，若∠ABC=45°，则AE+DE的最小值为.
-
6、若一次函数y=2x-5的图象过点（a，b），则2a-b+10=.
-
7、某公司招聘一名技术人员，小丽笔试和面试的成绩分别为90分和85分，综合成绩按照笔试占60%，面试占40%进行计算，则小丽的综合成绩为分
-
8、如图是我国古代的一种铜制货币“五铢钱”，某古币爱好者收藏了5枚“五铢钱”，测得它们的质量（单位：g）分别为3.4，3.4，3.5，3.4，3.3.这组数据的众数为.
-
9、计算：÷=.
-
10、如图，在平面直角坐标系中，四边形ABCD是平行四边形，的坐标为 ， 的坐标为 ， 点落在轴的正半轴上，点落在第一象限内，按如图所示的步骤作图，则点的坐标为（ ）
A、 B、 C、 D、 -
11、如图是小英爸爸设置的手机手势密码图，已知左右、上下两个相邻密码点间的距离均为1，手指沿A-B-C-D顺序解锁，按此手势解锁一次的路径长为（ ）
A、5 B、3+ C、3+ D、6 -
12、如图，在Rt△ABC中，∠ABC=90°，BD为斜边AC上的中线.若∠A=40°，则∠DBC=（ ）
A、40° B、45° C、50° D、55° -
13、矩形具有而一般平行四边形不具有的性质是（ ）A、对边相等 B、对角相等 C、对角线平分 D、对角线相等
-
14、已知正比例函数y=3x，则当-1≤x≤2时，函数的最大值为（ ）A、-6 B、-3 C、3 D、6
-
15、下列各组线段中，不能构成直角三角形的是（ ）A、2，4，5 B、1， ， 2 C、5，12，13 D、3，4，5
-
16、已知□ABCD的周长为10，其中AB=3，则BC=（ ）A、1 B、2 C、3 D、5
-
17、甲、乙两人10次标枪的落点如图所示，则甲、乙两人成绩方差的描述正确的是（ ）
A、 B、 C、 D、无法确定 -
18、下列各式是最简二次根式的是（ ）A、 B、 C、 D、
-
19、二次根式有意义，则x的取值范围是（ ）A、 B、 C、 D、
-
20、如图，两个等腰直角△ABC和△CDE中，∠ACB=∠DCE=90°
(1)、观察猜想如图1，点E在BC上，线段AE与BD的数量关系是；位置关系是.(2)、探究证明把△CDE绕直角顶点C旋转到图2的位置，（1）中的结论还成立吗？说明理由；(3)、拓展延伸：把△CDE绕点C在平面内自由旋转，若AC=BC=25，DE=14，当A、E、D三点在直线上时，请直接写出AD的长.