相关试卷

1、如图所示，一个可以自由转动的转盘被等分成16个小扇形，并分别涂上颜色。

(1)、转动转盘。指针停留在红色区域是事件，指针停留在绿色区域是事件：（从“随机”“必然”“不可能”中选填）

(2)、转动转盘。指针停留在蓝色区域的概率为.

(3)、若要通过涂改若干个小扇形的颜色，使指针停留在蓝色区域的概率是停留在红色区域的概率的两倍，请提供一种涂改方案，并说明理由.

查看解析
2、先化简，再求值：
$(2 x^{3} y - 4 x^{2} y^{2}) \div 2 x y - (x - 2) (x + 2)$ ，其中 $x = - 3$ ， $y = \frac{1}{2}$ .

查看解析
3、计算：

(1)、 ${(\frac{1}{3})}^{- 2} - {(- 2)}^{3} + {(2025 - π)}^{0} + | - 3 |$ ；

(2)、 $(2 a^{2})^{3} + 6 a^{3} (a^{3} - 2 a^{2} + a)$ .

查看解析
4、如图，在△ABC中，CD平分∠BCA，点E是BA的中点、过点E作EG//CD，交BC的延长线于点G，若CF= $\frac{1}{4}$ AF =1，则BC=.

查看解析
5、如图是一个非机动车的交通指示牌，自行车车架的支撑部分可以看成两个共边的三角形，若AD//BC，DB=DC，∠A=∠BDC=40°，则∠ABD=.

查看解析
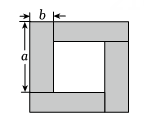
6、如图，4个长为a，宽为b的小长方形围成了一个大正方形，若а+b=16，ab=48，则a-b=.

查看解析
7、某学校七年级举行班级合唱比赛，组委会决定通过抽签的方式确定10个参赛班级的出场顺序，则七年级（2）班抽到前3个出场的概率为.

查看解析
8、已知三角形中两条边的长度分别为3和8，则此三角形的第三边的长度可能是。（写出一个值即可）

查看解析
9、如图，Rt△ABC中，∠BAC=90°，AB=AC，D为平面上一点，连接CD，点E为CD中点，连接AE，AD，BD、BE，AD=AE，且∠DAE=90°，若CD=6，则△BEC的面积为（）

A、3 B、2 C、 $\frac{9}{2}$ D、 $\frac{9}{4}$

查看解析
10、某实验室记录某液体在冷却过程中温度随时间变化的数据如下表：
冷却时间（分钟）
0
1
2
3
4
5
……
液体温度（℃）
100
80
65
55
50
48
……
下列说法错误的是（）

A、冷却时间是自变量，液体温度是因变量 B、0～2分钟，温度平均每分钟下降15℃ C、3～5分钟，温度下降速度逐渐减慢 D、第6分钟时，温度可能为47℃

查看解析
11、若（2x+m）·（x-2）的展开式中不含x项，则实数m的值为（）

A、2 B、-2 C、-4 D、4

查看解析
12、如图，下列判断中，错误的是（）

A、若∠1=∠2，则 CE∥BF B、若∠A=∠C，则AB//CD C、若∠B+∠BFC=180°，则AB//CD D、若∠A=∠D，则AB//CD

查看解析
13、数学学习小组在课外时间继续开展“掷假子”的数学实验。记录了“点数为6”的出现次数。如下表所示：
实验次数
100
200
500
1000
2000
点数为6的次数
18
32
95
170
334
根据以上数据，下列说法错误的是（）

A、随着实验次数增加，“点数为6”出现的频率会在一个常数附近摆动 B、当实验次数为500时，“点数为6”出现的须数为95 C、若再进行1000次的实验，“点数为6”出现的频率一定是0.17 D、估计“点数为6”出现的概率约为16.7%

查看解析
14、下列各式运算正确的是（）

A、2a²-3a²= a² B、a⁶÷a²=a⁴ C、（-a³）²=-a⁶ D、a²·a³= a⁶

查看解析
15、据新闻报道：我国科研团以成功制备了多种单原子层金属，厚度仅为头发丝直径的二十万分之一。若铅原子的直径约为0.00000000035米，该数据用科学记数法可表示为（）

A、3.5x10^-10米 B、3.5×10^-9米 C、35x10^-10米 D、35x10^-⁹米

查看解析
16、2025年。世界运动会将在中国四川成都举办。该运动会是一个以非奥运会项目为主要竞赛项目的国际体育盛事.下列竞赛项目图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看解析
17、如图1，直线AB与x轴交于点B（8，0），与y轴交于点A，直线CD与y轴交于点C，与直线AB交于点D，其中直线CD的解析式为 $y = \frac{1}{2} x - \frac{3}{2}$ ， OA=4OC.点M是线段AD上一点（点M不与点A，D重合），过点M作x轴的垂线交直线CD于点N，以MN，MD为邻边作□MNPD，连接PO，PB.

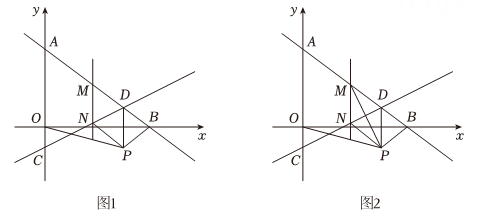(1)、求点D的坐标；

(2)、当△BPO的面积为3时，求点M的坐标；

(3)、如图2，连接PM，求证：PM⊥ND.

查看解析
18、如题图1，在正方形ABCD中，点P在边CD上，点M在边BC上，点N在边AD上，连接AP，MN交于点O，且MN⊥AP.

(1)、求证：PD+ND=MC：

(2)、如图2，若AB=4，点O为线段AP的中点，OD= $\sqrt{5}$ ，求BM的长.

查看解析
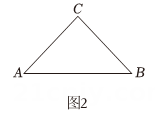
19、【阅读理解】中国古代数学家刘徽在《九章算术》中，给出了证明三角形面积公式的“出入相补法”，原理如下：如图，在△ABC中，点D，E分别是AB，AC的中点，连接DE，过点A作AF⊥DE于点F，延长FD至点M，使DM=DF，连接MB，延长FE至点N，使EN=EF，连接CN，则易证四边形BCNM的面积等于△ABC的面积，进一步可证三角形面积公式.

(1)、求证：四边形BCNM为矩形；

(2)、若DE=4，AF=3，求四边形BCNM的面积.

查看解析
20、定义：在△ABC中，BC=a，AC=b，AB=c，若a²+ab=c² ，则称△ABC为“类直角三角形”，请根据以上定义解决下列问题：

(1)、如图1，△ABC为等边三角形，请判断该三角形是否为“类直角三角形”，并说明理由；

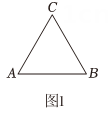(2)、如图2，等腰三角形△ABC为“类直角三角形”，其中AC=BC，AB>AC，请
求出∠B的大小。

查看解析

上一页 432 433 434 435 436 下一页跳转

冷却时间（分钟）	0	1	2	3	4	5	……
液体温度（℃）	100	80	65	55	50	48	……

实验次数	100	200	500	1000	2000
点数为6的次数	18	32	95	170	334