-
1、如图，在△ABC中，分别过点 B，A 作 BD⊥AC于点 D，AE⊥BC于点 E，BD，AE交于点 F.若∠BAC=45°，AD=5，CD=2，则线段 BF的长度为 ( )
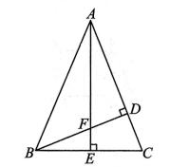A、2 B、 C、3 D、 -
2、
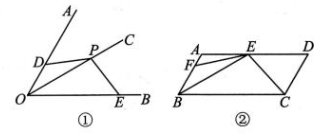(1)、如图①，已知 OC 是∠AOB 的平分线，P是OC上任意一点，点D，E分别在边 OA，OB 上，连 结 PD，PE，∠AOB +∠DPE=180°.若∠AOB=60°，OD+OE= ， 则OP的长为；(2)、如图②，在▱ABCD 中，∠ABC=60°，BE平分∠ABC交AD 于点E，连结CE，将CE 绕点 E 旋转，当点 C 的对应点 F 落在边AB 上时，若 求四边形BCEF的面积. -
3、 在△ABC中，AB=AC，∠BAC=90°，BD平分∠ABC交AC于点 D.
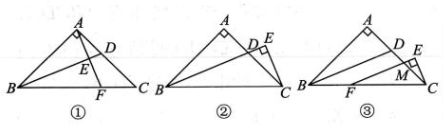(1)、如图①，F 为 BC 上一点，连结 AF交BD于点E.若AB=BF，求证：BD垂直平分AF；(2)、如图②，CE⊥BD，垂足 E 在 BD 的延长线上，试判断线段CE，BD 之间的数量关系，并说明理由；(3)、如图③，F 为 BC 上一点，∠EFC= ∠ABC，CE⊥EF，垂足为E，EF与AC 交于点M.直接写出线段CE，FM之间的数量关系. -
4、 如图，四边形 ABCD为平行四边形，∠BAD的平分线AF交CD 于点E，交 BC的延长线于点 F，连结 BE.若 BE⊥AF，EF= ， 则AB的长为.
-
5、如图，AE，BE，CE分别平分∠BAC，∠ABC，∠ACB，ED⊥BC于点D，ED=3，△ABC的面积为 36，则△ABC的周长为 ( )
A、48 B、36 C、24 D、12 -
6、如图，在△ABC中，AD平分∠BAC，E 是BC的中点，BD⊥AD 于点D.若AC=7，AB=4，则DE的长为 ( )
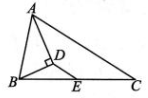A、1 B、2 C、 D、 -
7、 【阅读材料】
问题
如图，AB，CD 相交于点O，O 是 AB 的中点，AC∥BD，求证：O是CD 的中点.
问题分析
由条件易证△AOC≌△BOD，从而得到OC=OD，即O是CD 的中点.
方法提取
构造“平行8字形”全等三角形模型是证明线段相等的一种常用方法.
请运用上述阅读材料中获取的经验和方法解决下列问题.
【基础应用】
已知在△ABC中，. 点 E 在边 AB 上，点F 在边 BC的延长线上，连结EF交AC 于点 D.
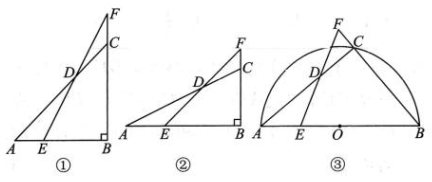(1)、如图①，若AB=BC，AE=CF，求证：D是EF的中点；(2)、如图②，若AB=2BC，AE=2CF，探究CD 与 BE 之间的数量关系；(3)、【灵活应用】如图③，AB是半圆O的直径，C是半圆上一点，E 是AB 上一点，点 F 在 BC 的延长线上， 当点C从点B运动到点A，点D运动的路径长为 ， CF 扫过的面积为.
-
8、如图，在 Rt△ABC 中，∠ACB=90°，AB=2，若 D 为直线 AC左侧一点，当△ABC∽△CAD时，BC+CD的最大值为 ( )
A、 B、 C、 D、 -
9、对于一元二次方程，我国古代数学家还研究过其几何解法.以方程x(x+6)=72为例加以说明.数学家赵爽在其所著的《勾股圆方图注》中记载的方法是：如图，将四个长为x+6，宽为x的矩形纸片拼成一个大正方形，则大正方形的边长是x+6+x，面积是四个矩形的面积与中间小正方形的面积之和，即 据此易得 小明用此方法解关于x的方程x(3x-n)=24，其中3x-n>x构造出同样的图形，已知小正方形的面积为4，则n的值为 ( )
A、2 B、4 C、6 D、8 -
10、在每个小正方形的边长均为1的网格图形中，每个小正方形的顶点称为格点.如图，在6×6的正方形网格图形ABCD中，M，N分别是AB，BC上的格点，BM=4，BN=2.若P是这个网格图形中的格点，连结PM，PN， 则 所 有 满 足 ∠MPN = 45°的△PMN中，边 PM的长的最大值是 ( )
A、4 B、6 C、 D、3 -
11、老师布置的作业中有这样一道题：
甲同学认为AB，AC，AD这三条线段不在同一个三角形中，无法解答，老师给的题目有错误；乙同学认为可以从中点D出发，构造辅助线，利用全等的知识解决；丙同学认为没必要借助全等三角形的知识，只需取 AB 的中点构造三角形的中位线，就可以解决.关于三位同学的思考过程，你认为正确的是 ( )
A、甲 B、乙 C、丙 D、乙和丙 -
12、在学习锐角三角函数时，小明同学对“具有倍半关系的两个锐角的正切值之间具有怎样的关系”这个问题产生了浓厚的兴趣，并进行了一些研究.
(1)、初步尝试：我们知道： ， ；发现结论： tan A ((填“=”或“≠”).
(2)、如图，在Rt△ABC中，∠C=90°，AC=2，BC=1，求 的值.研究思路：小明想构造包含 的直角三角形，延长CA至点 D，使得 DA=AB，连结BD，所以得到 即转化为求∠D的正切值，那么.
(3)、在△ABC 中，∠A 为锐角， ∠B=2∠A，AB=3 ， 求 S△ABC的值. -
13、在《九章算术》“割圆术”中指出：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这里所用的割圆术所体现的是一种由有限到无限的转化思想.比如在求 的和中，“…”代表按此规律不断求和.我们可设 则有 即 解得x=2，故
类似地，请你计算： .(直接填计算结果即可)
-
14、如图是钉板示意图，每相邻4 个钉点是边长为1个单位长度的小正方形的顶点，钉点A，B的连线与钉点C，D的连线交于点E，则
(1)、AB 与CD 是否垂直? (填“是”或“否”)；(2)、AE=. -
15、如图，已知 C为圆锥母线 SB 的中点，AB 为底面圆的直径，SB=6，AB=4，一只蚂蚁沿着圆锥的侧面从点A 爬到点C，则蚂蚁爬行的最短路程为（ ）
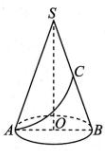A、5 B、 C、 D、 -
16、如图，△ABC 是边长为 4的等边三角形，点 D，E，F分别在边 AB，BC，CA 上运动，且满足 AD=BE=CF.
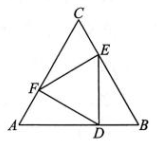(1)、求证：△ADF≌△BED；(2)、设AD 的长为x，△DEF的面积为y，求y关于x的函数表达式；(3)、结合(2)所得的函数，描述△DEF的面积随AD 的增大如何变化. -
17、图①是1个纸杯和6个叠放在一起的纸杯的示意图，量得1个纸杯的高为10cm，6个叠放在一起的纸杯的高为14 cm.
(1)、求3 个叠放在一起的纸杯的高为多少厘米.(2)、若设x个叠放在一起的纸杯的高为y cm(如图②)，并将这x个叠放在一起的纸杯按如图③所示的方式放进竖立的方盒中，方盒的厚度不计.①求y关于x的函数表达式；
②若竖立的方盒的高为 33.5 cm，求 x 的最大值.
-
18、如图所示，在Rt△ABC中，∠C=90°，BC1.若点 B1 刚好落在边AC上，且∠CB1E=30°，CE=m，则BC的长为.(用含m的代数式表示)
-
19、如图，⊙O 是四边形ABCD 的外接圆，AD=CD，连结 BD，过点A 作 BD的平行线交⊙O 于点 E，交 CB 的延长线于点 F，连结 DE.
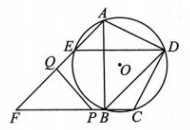(1)、求证：四边形 BDEF 是平行四边形.(2)、若∠F=45°，EF=2AE=m.①用含 m 的代数式表示BC 的长；
②点 P，Q分别在线段CF，AF 上，且 FQ= PC.当△QPF 与△BCD 相似时，求 的值.
-
20、某商店销售 A 型和 B 型两种电脑，其中 A型电脑每台的利润为 400 元，B型电脑每台的利润为500元.该商店计划一次性购进这两种型号的电脑共100 台，其中 B型电脑的进货量不超过 A 型电脑的 2 倍.设购进 A型电脑x台，这100 台电脑的销售总利润为y元.(1)、求y关于x 的函数关系式；(2)、该商店购进A 型，B型电脑各多少台，才能使销售总利润最大?最大利润是多少?(3)、实际进货时，厂家对 A 型电脑出厂价下调a(0<a<200)元，且限定商店最多购进 A型电脑60台，若商店保持同种电脑的售价不变，请你根据以上信息，设计出使这100台电脑的销售总利润最大的进货方案.