-
1、 的倒数是 , 相反数是 .
-
2、数轴上点所表示数的数是 , 点到点的距离是 , 则点所表示的数是 .
-
3、如图,数轴上有 , , , 四个整数点即各点均表示整数 , 且若 , 两点所表示的数分别是和 , 则到点所表示的数是( )
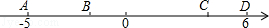 A、 B、 C、 D、
A、 B、 C、 D、 -
4、在数轴上表示的点离开原点的距离等于( )A、 B、 C、 D、
-
5、在 , , , , , 中,负分数有( )A、个 B、个 C、个 D、个
-
6、已知是最小的正整数,是最大的负整数,是绝对值最小的有理数,那么等于( )A、 B、 C、 D、
-
7、下列计算结果是负数的是( )A、 B、 C、 D、
-
8、下列等式计算正确的是( )A、 B、 C、 D、
-
9、下列各数中,在和之间的数是( )A、 B、 C、 D、
-
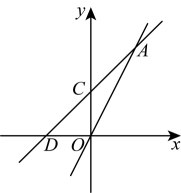
10、如图,已知直线:与y轴交于点A , 且和直线:交于点 , 根据以上信息解答下列问题:
 (1)、求a的值;(2)、不解关于x , y的方程组 , 请你直接写出它的解;(3)、若直线 , 表示的两个一次函数都大于0,此时恰好 , 求直线的函数解析式.
(1)、求a的值;(2)、不解关于x , y的方程组 , 请你直接写出它的解;(3)、若直线 , 表示的两个一次函数都大于0,此时恰好 , 求直线的函数解析式. -
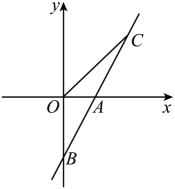
11、如图,正比例函数的图象与一次函数的图象交于点 , 一次函数图象与y轴的交点为 , 与x轴的交点为D .
 (1)、求一次函数的表达式;(2)、一次函数的图象上是否存在点P , 使得 , 若存在,求出点P的坐标;若不存在,说明理由.
(1)、求一次函数的表达式;(2)、一次函数的图象上是否存在点P , 使得 , 若存在,求出点P的坐标;若不存在,说明理由. -
12、如图,直线与轴交于点 , 与轴交于点 .
 (1)、求直线的表达式;(2)、若直线上的点在第一象限,且 , 求点的坐标.
(1)、求直线的表达式;(2)、若直线上的点在第一象限,且 , 求点的坐标. -
13、在平面直角坐标系中,一次函数(都是常数,且)的图象经过点和(1)、求一次函数的表达式;(2)、已知点在该函数的图象上,求点P的坐标.
-
14、小明在游乐场坐过山车,某一分钟内过山车高度h(米)与时间(秒)之间的函数图象如图所示,请结合图象回答:
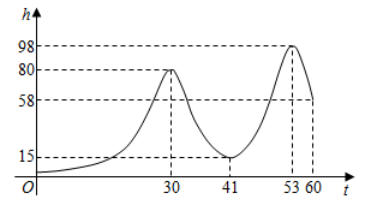 (1)、过山车所达到的最大高度是多少?(2)、请描述秒后,高度(米)随时间(秒)的变化情况
(1)、过山车所达到的最大高度是多少?(2)、请描述秒后,高度(米)随时间(秒)的变化情况 -
15、已知y是x的正比例函数,当x=﹣3时,y=12.(1)、求y关于x的函数解析式;(2)、当时的函数值.
-
16、若与x+1成正比例,且x=1是y=5,求y与x的函数表达式.
-
17、利用图象求方程组的解.
-
18、已知一次函数与(k是常数,)的图象的交点坐标是 , 则方程组的解是 .
-
19、已知点和点是图象上的两个点,则与 的大小关系 .
-
20、已知一次函数 , 当时, , 则m的值为 .