-
1、已知正数x的两个不等的平方根分别是和 , 的立方根为;c是的整数部分,若 , 其中m为整数, , 则 .
-
2、近似数 是精确到( )A、千分位 B、千位 C、百位 D、十位
-
3、若m,n为实数,且 , 则的值为( )A、1 B、0 C、81 D、
-
4、如果 , 那么的立方根是( )A、1 B、 C、 D、
-
5、某人的体重约为 , 这个数是个近似数,那么这个人的体重的取值范围是( )A、 B、 C、 D、
-
6、下列说法中,错误的是( )A、5是25的算术平方根 B、的平方根是 C、0的平方根与算术平方根都是0 D、的平方根是
-
7、下列各式中,正确的是( )A、 B、 C、 D、
-
8、已知为直线上一点,以为端点作射线 , 使 , 将一个直角三角尺的直角顶点放在点处.
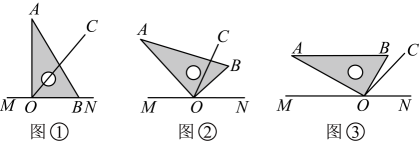 (1)、如图①,若直角三角尺的一边与射线重合,则;(2)、将直角三角尺摆放至如图②所示的位置时,恰好平分 , 请判断是否平分 , 并说明理由;(3)、将直角三角尺摆放至如图③所示的位置时,若恰好 , 求的度数.
(1)、如图①,若直角三角尺的一边与射线重合,则;(2)、将直角三角尺摆放至如图②所示的位置时,恰好平分 , 请判断是否平分 , 并说明理由;(3)、将直角三角尺摆放至如图③所示的位置时,若恰好 , 求的度数. -
9、
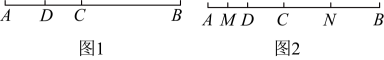 (1)、如图1,点C为线段上一点,与长度之比为3:5,D为线段中点.
(1)、如图1,点C为线段上一点,与长度之比为3:5,D为线段中点.①若 , 求的长.
②点E为线段的中点,若 , 求的长(用含m的代数式表示).
(2)、如图2,点M为线段中点,点N为线段中点,若 , , 请用含a , b的代数式直接表示出的长. -
10、在平整的地面上,有若干个完全相同的棱长为的小正方体堆成一个几何体,如图所示:
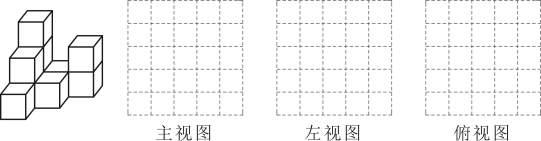 (1)、这个几何体是由 个小正方体组成,该几何体的体积是 , 请用阴影画出这个几何体从三个方向看的图形;(2)、如果在这个几何体露在外面的表面喷上红色的漆,每平方厘米用2克,则共需克漆;(3)、如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加个小正方体.
(1)、这个几何体是由 个小正方体组成,该几何体的体积是 , 请用阴影画出这个几何体从三个方向看的图形;(2)、如果在这个几何体露在外面的表面喷上红色的漆,每平方厘米用2克,则共需克漆;(3)、如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加个小正方体. -
11、根据所给立体图形的三视图,
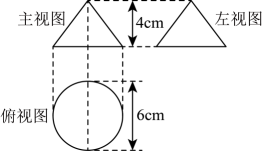 (1)、写出这个立体图形的名称:;(2)、求出这个立体图形的体积.
(1)、写出这个立体图形的名称:;(2)、求出这个立体图形的体积. -
12、如图,是的平分线, .
 (1)、若 , 求的度数.(2)、若 , 求的度数.
(1)、若 , 求的度数.(2)、若 , 求的度数. -
13、已知线段 , 点C为线段上的一个动点(点C不与A、B重合),点D、E分别是和的中点(1)、若 , 求的长;(2)、若点C恰好是的中点,且 , 求的长.
-
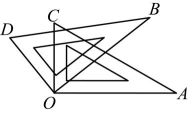
14、如图,两个直角三角尺的直角顶点重合.如果 , 那么 .
-
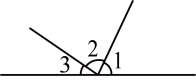
15、如图,若 , , 则的度数为 .
-
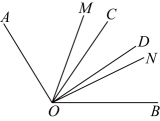
16、如图, , 在内作两条射线和 , 且平分平分 , 若 , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
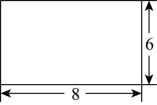
17、如图,长方形是一个圆柱体的侧面展开图,则这个圆柱体的体积为( )
 A、 B、或 C、 D、或
A、 B、或 C、 D、或 -
18、如图,、是线段上两点,、分别是线段 , 的中点,下列结论:①若 , 则;②若 , 则;③ . 其中正确的结论是( )
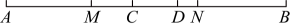 A、① B、② C、①③ D、①②③
A、① B、② C、①③ D、①②③ -
19、如图,O是直线上一点,平分 , , 则图中互余的角、互补的角各有( )对.
 A、3,3 B、4,7 C、4,4 D、4,5
A、3,3 B、4,7 C、4,4 D、4,5 -
20、图是正方体的展开图,相对面上的多项式的和相等,则A等于( )
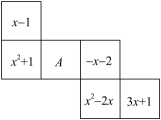 A、 B、 C、 D、
A、 B、 C、 D、