-
1、若沿河两地相距 ， 船在静水中的速度为 ， 水流的速度为 ， 则船在两地之间往返一次所需的时间是（ ）A、 B、 C、 D、
-
2、化简（ ）A、 B、 C、 D、
-
3、下列各式中，不论取何值，分式都有意义的是（ ）A、 B、 C、 D、
-
4、在式子 ， ， ， ， ， ， 中，分式的个数是（ ）A、2 B、3 C、4 D、5
-
5、如图1，AB=7 cm，AC=5 cm，AC⊥AB，BD⊥AB，垂足分别为A，B.点P在线段AB上以2 cm/s的速度由点A向点B运动，同时，点Q在射线BD上运动.它们运动的时间为t s，当点P运动结束时，点Q运动随之结束.
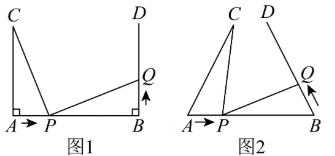(1)、若点Q的运动速度与点P的运动速度相同，当t=1时，△ACP与△BPQ是否全等?并判断此时线段PC和线段PQ的位置关系，请分别说明理由.(2)、如图2，若“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA=60°”，点Q的运动速度为x cm/s，其他条件不变，当点P，Q运动到某处时，有△ACP与△BPQ全等，求出相应的x，t的值. -
6、命题：全等三角形的对应边上的高相等.(1)、先把这个命题写成“如果……，那么……”的形式，再写出这个命题的逆命题.(2)、判断原命题的真假，如果是假命题，请举出一个反例；如果是真命题，请写出证明过程.
-
7、如图，∠A=∠B=50°，P为AB的中点，过点P作直线分别交射线AC，BD于点M，N(分别不与点A，B重合)，设∠BPN=α.
(1)、求证：PM=PN.(2)、当△APM为直角三角形时，求α的度数. -
8、如图，小明同学拿着老师的等腰直角三角尺，摆放在两摞长方体教具之间，∠ACB=90°，AC=CB，每个小长方体教具高度均为4 cm.
(1)、求证：△ACD≌△CBE.(2)、求DE的长. -
9、如图所示，已知线段a及∠α，求作△ABC，使AB=a，AC=2a，∠A=2∠α，写出作法，保留作图痕迹.
-
10、如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F.如果AB=10，AE=3，求线段CF的长度.
-
11、如图，AB=AD，∠BAC=∠DAC=25°，∠D=80°.求∠BCA的度数.
-
12、如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，已知EH=EB=4，S△AEH=12，则CH的长为.
-
13、如图，点B，E，C，F在同一直线上，△ABC≌△DEF，AC，DE交于点M.若∠B=50°，∠F=60°，则∠AMD的度数为.
-
14、如图，在△ABC中，点D在AB上，点E在BC上，且BD=BE，请你再添加一个条件，使得△BEA≌△BDC，你添加的条件是.(只需添加一个正确的即可)
-
15、如图，已知线段AB=18，MA⊥AB于点A，MA=6，射线BD⊥AB于点B，点P从点B向点A运动，每秒走1个单位长度，点Q从点B向点D运动，每秒走2个单位长度，点P，Q同时从点B出发，若出发x s后，在线段MA上有一点C，使△CAP与△PBQ全等，则x的值为( )
A、4 B、6 C、4或9 D、6或9 -
16、如图，在四边形ABCD中，AB∥CD，∠1=∠2，AD=CE.若AB=2，BE=3，则CD的长为( )
A、4 B、5 C、6 D、7 -
17、如图是一个正方形网格，每个小正方形的边长相等，我们把该网格中正方形的顶点称之为“好点”，△ABC的三个顶点都在这个正方形网格的“好点”上，在这个正方形网格图中找一个“好点”D(点D与点A不重合)，使得以点D，B，C为顶点的三角形与△ABC全等，则这样的“好点”D的个数为( )
A、1 B、2 C、3 D、4 -
18、如图，已知点B，C，E在同一条直线上，∠B=∠E=∠ACD=60°，AB=CE，则图中与BC相等的线段是( )
A、AC B、DE C、DC D、AD -
19、如图，在△ABC和△DEF中，点B，C，E，F在同一条直线上，AB=DE，AC=DF，BE=CF，∠A=95°，∠DEF=15°，则∠F的度数为( )
A、25° B、60° C、70° D、95° -
20、如图，一块三角形的玻璃打碎成四块，现要到玻璃店去配一块与原来完全一样的玻璃，最简单的办法是( )
A、只带①去 B、带②③去 C、带①③去 D、只带④去