-
1、如图,在一个底为a,高为h的三角形铁皮上剪去一个半径为r的半圆.
 (1)、用含有a,h,r的代数式表示剩下铁皮(阴影部分铁皮)的面积S;(2)、请求出当 , , 时,S的值(结果保留).
(1)、用含有a,h,r的代数式表示剩下铁皮(阴影部分铁皮)的面积S;(2)、请求出当 , , 时,S的值(结果保留). -
2、已知当:时,代数式的值为7,则当时,代数式的值为 .
-
3、用同样大小的黑色棋子按如图所示的方式摆放,按照这样的规律摆下去,则第2024个图形需棋子枚.

-
4、若与互为相反数,与互为倒数,的倒数为它本身,求 .
-
5、若关于b的单项式与相加等于0,则 .
-
6、我国末朝时期的数学家杨辉,曾将大小完全相同的圆弹珠逐层堆积、形成“三角垛”、图1有1颗弹珠:图2有3颗弹珠:图3有6颗弹珠,往下依次是第4个图,第5个图,…;若用表示图n的弹珠数,其中 , 2, 3, …,则 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、已知:关于x,y的多项式不含二次项,则的值是( )A、0 B、12 C、 D、8
-
8、一个多项式与的和是 , 则这个多项式为( )A、 B、 C、 D、
-
9、如果多项式是关于的三次三项式,那么的值为( )A、 B、 C、 D、
-
10、已知数 , , 在数轴上的位置如图,下列说法:
①;②;③;④ . 其中正确结论序号是( )
 A、①④ B、②③ C、②③④ D、①③④
A、①④ B、②③ C、②③④ D、①③④ -
11、已知 , 则的值是( )A、 B、6 C、18 D、
-
12、如果关于x,y的两个单项式与的和是一个单项式,那么m,n的值分别为( )A、 B、 C、 D、
-
13、下列代数式中,不是整式的为( )A、 B、 C、 D、
-
14、定义:已知M,N都是关于x的多项式,若( , 且k不含字母),则称M是N的“平移式”,k叫做M关于N的“平移值”.例如: , , , 则称M是N的“平移式”,M关于N的“平移值”为4.(1)、若 , , 则M是N的“平移式”吗?为什么?(2)、对于常数m,n,有 , , 若M是N的“平移式”,且“平移值”为3,求m,n的值;(3)、若A,B,M都是关于x的多项式,且 , . , 且 , 试问:M是N的“平移式”吗?如果是,求出m,n的值及“平移值”;如果不是,请说明理由.
-
15、如图1,在数轴上点M表示的数为m,点N表示的数为n,点M到点N的距离记为 , 即 . 如图2,在数轴上点A表示数a,点B表示数b,点C表示数c,a是3的相反数,b是最大的负整数,c是多项式的次数.
 (1)、 , , .(2)、x是数轴上任意一个有理数,则有最小值是 , 有最大值是 , 当取得最大值时相应的有理数x的取值范围是 .(3)、如图 , 点E,F,G是数轴上的三点,E点表示数是 , F点表示数是 , G点表示数是 , 点E,F,G同时开始在数轴上运动,若点E以每秒个单位长度的速度向左运动,点F和点G分别以每秒个单位长度和个单位长度的速度向右运动,假设t秒后,若点E与点F之间的距离表示为 , 点E与点G之间的距离表示为 , 点F与点G之间的距离表示为 . 若的值是一个定值,请求出m的值.
(1)、 , , .(2)、x是数轴上任意一个有理数,则有最小值是 , 有最大值是 , 当取得最大值时相应的有理数x的取值范围是 .(3)、如图 , 点E,F,G是数轴上的三点,E点表示数是 , F点表示数是 , G点表示数是 , 点E,F,G同时开始在数轴上运动,若点E以每秒个单位长度的速度向左运动,点F和点G分别以每秒个单位长度和个单位长度的速度向右运动,假设t秒后,若点E与点F之间的距离表示为 , 点E与点G之间的距离表示为 , 点F与点G之间的距离表示为 . 若的值是一个定值,请求出m的值.
-
16、【教材呈现】“整体思想”是数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.下题是华师版七年级上册数学教材第120页的部分内容.
代数式的值为7,则代数式的值为▲ .
【阅读理解】小明在做作业时采用的方法如下:由题意得,则有 , , 所以代数式的值为5.
(1)、【方法运用】若代数式的值为15,求代数式的值.
(2)、若时,代数式的值为19,当时,求代数式的值.(3)、【拓展应用】若 , . 则的值为 .
-
17、点在数轴上的位置如图所示,其对应的数分别是和 .
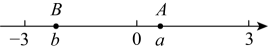 (1)、化简:;(2)、若 , 到的距离是1个单位长度,、互为相反数,、互为倒数,求代数式的值.
(1)、化简:;(2)、若 , 到的距离是1个单位长度,、互为相反数,、互为倒数,求代数式的值. -
18、已知多项式 , .(1)、若的值与x的取值无关,求m,n的值;(2)、在(1)的条件下,求的值.
-
19、已知代数式 .(1)、化简;(2)、若满足等式 , 求的值.
-
20、如图,小长方形纸片的长为a,宽为b,且 , 将7张纸片按图示不重叠的放在长方形内,未被覆盖的部分恰好被分割为两个长方形,面积分别为和 .
 (1)、当 , , 时,的值为 ;(2)、若长度保持不变,变长,将这7张小长方形纸片还按照同样的方式放在新的长方形内,当的值与的长度无关时,a、b满足的关系式是 .
(1)、当 , , 时,的值为 ;(2)、若长度保持不变,变长,将这7张小长方形纸片还按照同样的方式放在新的长方形内,当的值与的长度无关时,a、b满足的关系式是 .