-
1、如果一组数据6，7，x，9，5的平均数是2x，那么这组数据的标准差为( )A、4 B、3 C、2 D、1
-
2、甲、乙、丙、丁四位优秀短跑选手近期10次的百米测试平均成绩都是10.3秒，但他们成绩的方差分别是0.020，0.019，0.021，0.022(单位：秒2).则这四人中发挥最稳定的是( )A、甲 B、乙 C、丙 D、丁
-
3、某地2022年1月9日的最高气温为4 ℃，最低气温为-10 ℃，则该日的气温极差为( )A、4 ℃ B、6 ℃ C、10 ℃ D、14 ℃
-
4、某天上午8：00小李从家中出发，以2 m/s的速度于8：15到达商店，然后以2.5 m/s的速度于8：20到达书店，则小李从家到书店的平均速度为( )A、2.25 m/s B、2.125 m/s C、2.175 m/s D、2.225 m/s
-
5、某校开展安全知识竞赛，进入决赛的学生有20名，他们的决赛成绩如表所示，则这20名学生决赛成绩的中位数和众数分别是( )
决赛成绩/分
100
99
98
97
人数
3
7
6
4
A、98，98 B、98，99 C、98.5，98 D、98.5，99 -
6、若5个数的平均数为8，则将其中一个数据12去掉，余下数据的平均数是( )A、6 B、7 C、8 D、9
-
7、一次知识竞赛中，小明的成绩为72分，超过班级半数同学的成绩，分析得出这个结论所用的统计量是( )A、中位数 B、众数 C、平均数 D、方差
-
8、定义：在一个三角形中，如果有一个角是另一个角的 ， 那么我们就称这两个角互为“友爱角”，这个三角形为“友爱三角形”.例如：在△ABC中，如果∠A=80°，∠B=40°，那么∠A与∠B互为“友爱角”，△ABC为“友爱三角形”.
①
②
(1)、如图①所示，△ABC是“友爱三角形”，且∠A与∠B互为“友爱角”(∠A>∠B)，∠ACB=90°.①求∠A，∠B的度数.
②若CD是△ABC中AB边上的高，则△ACD，△BCD都是“友爱三角形”吗?为什么?
(2)、如图②所示，在△ABC中，∠ACB=70°，∠A=66°，D是边AB上一点(不与点A，B重合)，连接CD，若△ACD是“友爱三角形”，直接写出∠ACD的度数. -
9、如图所示，A，B两点分别位于一池塘两侧，池塘左边有一水房D，在DB中点C处有一棵百年古槐，小明从A点出发，沿AC一直向前走到点E(A，C，E三点在同一条直线上)，并使CE=CA，然后他测量出点E到水房D的距离，则DE的长度就是A，B两点间的距离.
(1)、如果小明恰好未带测量工具，但他知道水房D和古槐C到A点的距离分别是140 m和100 m，他能不能确定AB的长度范围?如果能，求出AB的长度范围；如果不能，请说明理由.(2)、在(1)的解题过程中，你找到“已知三角形一边和另一边上的中线，求第三边的长度范围”的方法了吗?如果找到了，请解决下面的问题：在△ABC中，AC=5，中线AD=7，画图并确定AB的长度范围. -
10、已知：如图所示，在△ABC和△DEF中，B，E，C，F在同一条直线上.有下面四个条件：
①AB=DE；②AC=DF；③BE=CF；④∠ABC=∠DEF.
(1)、请选择其中的三个条件，使得△ABC≌△DEF(写出一种情况即可).(2)、在(1)的条件下，试说明：△ABC≌△DEF. -
11、如图所示，点C在线段AD上，AB=AD，∠B=∠D，BC=DE.
(1)、试说明：△ABC≌△ADE；(2)、若∠BAC=60°，求∠ACE的度数. -
12、尺规作图：如图所示，已知线段a，b和∠α，用尺规作一个三角形，使其两边分别等于a，b，这两边的夹角等于2∠α.
要求：不写作法，只画图，保留作图痕迹.
-
13、如图所示，在长方形ABCD中，AB=4，AD=5，延长边BC到点E，使CE=2，连接DE.动点P从点B出发，以每秒2个单位长度的速度沿BC-CD-DA向终点A运动，当△ABP和△DCE全等时，△DCE会闪烁一下(闪烁时间极短，忽略不计)，则△DCE首次闪烁与第二次闪烁的时间间隔为秒.
-
14、如图所示，AE⊥AB且AE=AB，BC⊥CD且BC=CD，那么，按照图中所标注的数据，图中实线所围成图形的面积为.
-
15、已知∠α和线段a，用尺规作△ABC，使∠A=2∠α，AB=2a，∠B=3∠α.作法如下：
①在AN上截取AB=2a；②作∠MAN=2∠α；③以点B为顶点，BA为一边在∠MAN的同侧作∠ABE=3∠α，BE交AM于点C.△ABC即为所求.则正确的作图顺序是.(填序号)
-
16、如图所示，∠A=75°，∠B=65°，将纸片的一角折叠，使点C落在△ABC内部，若∠1=45°，则∠2=°.
-
17、如图所示，已知△ABC≌△DEF，点B，E，C，F依次在同一条直线上.若BC=8，CE=5，则CF的长为.
-
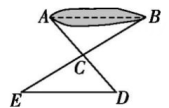
18、如图所示，有一池塘，要测池塘两端A，B的距离，可先在地上取一个点C，从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D，使CD=CA，连接BC并延长到点E，使CE=CB，连接DE.根据两个三角形全等，可知量出的DE的长就是A，B的距离.判定图中两个三角形全等的依据是.
-
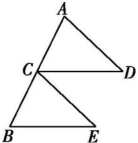
19、如图所示，C是AB的中点，且CD=BE，请添加一个条件 ， 使得△ACD≌△CBE.
-
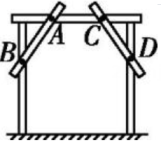
20、赵师傅做完门框后，为防止变形，按如图所示方式在门上钉上两根斜拉的木条(即图中的AB，CD两根木条)，这其中的数学原理是.
