-
1、如图所示,在平面直角坐标系中,平行四边形的顶点 , 的坐标分别是 , , , 则顶点的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图,在四边形中,点 , , , 分别是线段 , , , 的中点,则四边形的周长( )
 A、只与 , 的长有关 B、只与 , 的长有关 C、只与 , 的长有关 D、与四边形各边的长都有关
A、只与 , 的长有关 B、只与 , 的长有关 C、只与 , 的长有关 D、与四边形各边的长都有关 -
3、已知一个多边形的内角和是外角和的3倍,则此多边形的边数为( )A、8 B、7 C、6 D、5
-
4、如图,在中,是的平分线交于点 , 且 , 的周长是26,则( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
5、如图,在四边形中,对角线 , 相交于点 , 下列条件不能判定这个四边形是平行四边形的是( )
 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 , -
6、在中, ,则的度数是( )A、 B、 C、 D、
-
7、如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC 绕点C 顺时针旋转一定的角度α得到△DEC,点A,B的对应点分别是点D,E.
 (1)、如图1,当点 E恰好在AC 边上时,连接AD,求∠ADE的度数;(2)、如图2,点 F 是AC上一点,当旋转角α=60°且∠FBC=30°时,连接EB,DF,请判断四边形 BFDE 的形状,并说明理由.
(1)、如图1,当点 E恰好在AC 边上时,连接AD,求∠ADE的度数;(2)、如图2,点 F 是AC上一点,当旋转角α=60°且∠FBC=30°时,连接EB,DF,请判断四边形 BFDE 的形状,并说明理由. -
8、如图,在▱ABCD中,∠ABC的平分线与CD的延长线相交于点E,与AD 相交于点F,且点 F恰好为边AD 的中点,连接AE.
 (1)、求证:四边形ABDE 是平行四边形;(2)、若AG⊥BE于点G,BC=6,AG=2,求 EF的长.
(1)、求证:四边形ABDE 是平行四边形;(2)、若AG⊥BE于点G,BC=6,AG=2,求 EF的长. -
9、如图,在四边形 ABCD 中, 点 E 是BC的中点.点 P,Q分别是边AD,BC上的两点,其中点 P 以每秒1个单位长度的速度从点 A 运动到点D 后再返回点A,同时点 Q以每秒2个单位长度的速度从点 C出发向点 B 运动,当其中一点到达终点时停止运动.求:当运动时间t为多少秒时,以点 A,P,Q,E为顶点的四边形是平行四边形.

-
10、如图,将 沿过点A 的直线l 折叠,使点 D 落到AB 边上的点 处,折痕l交CD 边于点 E,连接BE.
 (1)、求证:四边形. 是平行四边形;(2)、若BE平分 求证:
(1)、求证:四边形. 是平行四边形;(2)、若BE平分 求证: -
11、如图,在△ABC中,AB=AC,D 是BA 延长线上的一点,E 是AC 的中点.
 (1)、实践与操作:利用尺规按下列要求作图,并在图中标明相应字母;(保留作图痕迹,不写作法)
(1)、实践与操作:利用尺规按下列要求作图,并在图中标明相应字母;(保留作图痕迹,不写作法)①作∠DAC的平分线AM;
②连接BE 并延长,交 AM 于点 F;
③连接FC;
(2)、猜想与证明:猜想四边形 ABCF 的形状,并说明理由. -
12、如图,▱ABCD的对角线AC与BD相交于点O,点E,F分别在OB 和OD 上,且∠AEB=∠CFD.
 (1)、求证:四边形AECF 是平行四边形;(2)、若∠AEB=90°,AE=EF=2,求线段AC的长.
(1)、求证:四边形AECF 是平行四边形;(2)、若∠AEB=90°,AE=EF=2,求线段AC的长. -
13、李师傅要为某单位修建正多边形花台,已知正多边形花台的一个外角的度数比一个内角度数的 多12°,请你 帮李师傅求出这个正多边形的一个内角的度数和它的对角线总数.
-
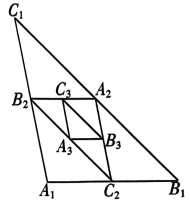
14、如图,在 中, 点 分别是边 的中点;点 分别是边 的中点⋯⋯以此类推,则 的周长是.
-
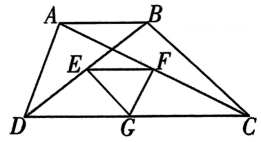
15、如图,在四边形ABCD中, ∥AD与 BC的和是12,点 E,F,G分别是 BD,AC,DC的中点,则 的周长是.
-
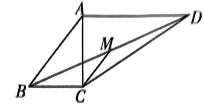
16、如图,在四边形ABCD 中, ∥M 为BD 的中点,则 CM 的长为.
-
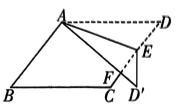
17、如图,在平行四边形ABCD中,E为边CD上一点,将 沿AE 折叠至 处, 与CE 相交于点 F,若则 的大小为.
-
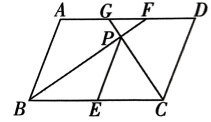
18、如图,在平行四边形ABCD 中, 的角平分线BF 交AD 于点F, 的角平分线CG 交AD 于点G,两条角平分线在平行四边形内部相交于点 P,连接 PE, 若 则GF的长为.
-
19、如图,点E,F分别放在 的边BC,AD上,AC,EF相交于点O,请你添加一个条件(只添一个即可),使四边形 AECF是平行四边形,你所添加的条件是.

-
20、如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF 都是等边三角形,下列结论:①AB⊥AC ②四边形AEFD是平行四边形 ③∠DFE=150° ④S四边形AEFD =8.其中错误的个数是 ( )
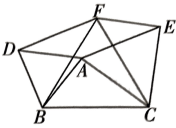 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个