相关试卷

1、仅用无刻度的直尺完成下列画图.

(1)、在图1中，经过格点A，B，C的圆与网格线交于点D.在 $\overset{⌢}{B C}$ 上画点F，使得AF=AD；

(2)、在图2中，经过格点A，B的圆与网格线交于点C，在. $\overset{⌢}{B C}$ 上画点P，使得 $\overset{⌢}{C P} = \overset{⌢}{A B}$

查看解析
2、仅用无刻度的直尺完成下列画图.

(1)、在图1中，⊙O与网格线交于点A，B，C 是⊙O上的一点，在 $\overset{⌢}{A C}$ 上画点E，使得 $\hat{A E} = \hat{B C};$

(2)、在图2中，经过格点 A，B，C的圆与网格线交于点D，在BC上画点F，使得DF=DA.

查看解析
3、仅用无刻度的直尺完成下列画图.

(1)、在图1中，P是经过格点A，B的圆上一点，先画出该圆的圆心O，再在⊙O上画点H，使得∠APH=45°，画出所有符合条件的点 H；

(2)、在图2中，O 是格点，在⊙O 上画一个15°的圆周角.

查看解析
4、如图，抛物线 $y = a x^{2} + b x + c$ 交x 轴于A(-1，0)，B(3，0)两点，交 y 轴于点C(0，-3)，Q 为线段BC 上的动点.

(1)、直接写出抛物线的解析式；

(2)、过点Q作PQ∥AC 交第四象限内的抛物线于点 P，连接 PA，PB，记△PAQ 与△PBQ面积分别为S₁ ， S₂ ，设. $S = S_{1} + S_{2},$ 当 S 最大时，求点 P 的坐标，并求 S 的最大值.

查看解析
5、如图，抛物线 $y = a x^{2} + b x - 8$ 与x轴交于A(-4，0)，B(2，0)两点，与 y轴交于点C. P 为第三象限内抛物线上一点，作直线AC，连接PA，PC，求△PAC 面积的最大值及此时点P 的坐标.

查看解析
6、如图，有一块五边形余料ABCDE，AB=AE=6，BC=5，∠A=∠B=90°，∠C=135°，∠E>90°.要在这答案块余料中截取一块矩形材料，其中一条边在AE 上，并使所截矩形材料的面积S 尽可能大.

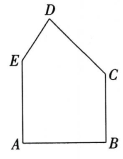(1)、若所截矩形材料的一条边是BC 或AE，求矩形材料的面积.

(2)、能否截出比(1)中更大面积的矩形材料?如果能，求出能截取矩形材料面积的最大值；如果不能，请说明理由.

查看解析
7、在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角(两边足够长)，用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB，BC两边).设AB=x m，花园的面积为S m².

(1)、若花园的面积为192m² ，求x 的值.

(2)、写出S 与x之间的函数表达式.当x 为何值时，S有最大值?最大值为多少?

(3)、若点 P 处有一棵树与墙CD，AD 的距离分别是a m(14≤a≤22)和6m ，要将这棵树围在花园内(含边界，不考虑树的粗细)，设S的最大值为y，求出 y 与a 之间的函数表达式.

查看解析
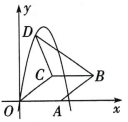
8、如图，在平面直角坐标系中，菱形OABC 的顶点A 在x轴的正半轴上，顶点C 的坐标为(4，3)，D 是抛物线 $y = - x^{2} + 6 x$ 上一点，且在x 轴上方，则△BCD 的面积最大为.

查看解析
9、如图①所示的矩形窗框 ABCD 的周长及其两条隔断EF，GH 的总长为a m，且隔断EF，GH 分别与矩形的两条邻边平行.设 BC 的长为x m，矩形 ABCD的面积为ym² ， y关于x 的二次函数图象如图②所示，则下列说法中，正确的是 ( )

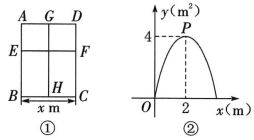A、矩形ABCD 的最大面积为8m² B、y与x之间的函数表达式为 $y = - x^{2} + 2 x$ C、当x=4时，矩形ABCD 的面积最大 D、a 的值为 12

查看解析
10、如图，景区内有一块矩形油菜花地，要在其中修建一条观花道(阴影部分)，供游人赏花.设改造后剩余油菜花地所占的面积为y m².若要求 0.5≤x≤1，求改造后剩余油菜花地所占的最大面积.

查看解析
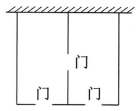
11、某农场拟建两间矩形饲养室，其中一面靠现有的墙(墙足够长)，中间用一道墙隔开，并在如图所示的三处各留一个 1m 宽的门.已知计划中的材料可建(不包括门)总长为27 m的墙体，则能建成的饲养室的面积最大为m².

查看解析
12、在某市治理违建的过程中，某小区拆除了自建房，改建绿地.如图，自建房占地是边长为8m的正方形 ABCD，改建的绿地是矩形AEFG，其中点 E 在AB上，点G在AD 的延长线上，且DG=2BE.当BE=m时，绿地AEFG 的面积最大.

查看解析
13、用48米长的木料制作如图所示的矩形窗框(横档 EF，GH 也用木料)，其中AB∥EF∥GH∥CD.若要使窗框ABCD 的面积最大，则AB 的长为( )

A、6米 B、8米 C、12 米 D、4 $\sqrt{3}$

查看解析
14、某班数学兴趣小组对函数 $y = ∣ x^{2} -$ 2x|的图象和性质进行了探究，探究过程如下：

(1)、自变量x 的取值范围是全体实数，x与y的几组对应值列表如下：
x
…
-1
-0.5
0
0.5
1
1.5
2
2.5
3
…
y
…
3
m
0
0.75
1
0.75
0
1.25
3
…
求上表中m 的值.

(2)、根据(1)中的数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分.

(3)、观察函数图象，写出该函数的一条性质.

(4)、通过进一步探究函数图象，解决下列问题：
①方程 $∣ x^{2} - 2 x ∣ = \frac{1}{2}$ 有个实数根.
②在(2)的平面直角坐标系中画出直线y=-x+1，根据图象及(1)中的数据可知，方程 $∣ x^{2} - 2 x ∣ = - x + 1$ 的一个正实数根约为 (结果精确到0.1).

查看解析
15、如图，二次函数 $y = a x^{2} + b x + c$ 的图象过A(2，0)，B(0，-1)和C(4，5)三点.

(1)、求二次函数的表达式.

(2)、设二次函数的图象与x轴的另一个交点为D，求点 D 的坐标.

(3)、在同一平面直角坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值.

查看解析
16、规定：如果两个函数的图象关于y轴对称，那么称这两个函数互为“Y函数”.例如：函数y=x+3与y=-x+3互为“Y 函数”.若函数 $y = \frac{k}{4} x^{2} + (k - 1) x + k - 3$ 的图象与x轴只有一个交点，则它的“Y函数”图象与x 轴的交点坐标为.

查看解析
17、二次函数 $y = x^{2} + b x$ 的图象如图所示，对称轴为直线x=1.若关于x 的一元二次方程 $x^{2} + b x - t = 0$ (b，t为实数)在-1<x<4的范围内有解，则t 的取值范围是.

查看解析
18、已知抛物线y=a(x-1)(x-5)+c(a≠0)与x 轴的一个交点为(2，0)，则方程 $x^{2} + 5 =$ $6 x - \frac{c}{a}$ 的解为 .

查看解析
19、数形结合思想如图，抛物线 $y = a x^{2} +$ bx+c(a≠0)的对称轴为直线x=2.若x₁ ， x₂是一元二次方程 $a x^{2} +$ bx+c=0(a≠0)的两个根，且x₁＜x_2，-1＜x₁<0，则下列说法中，正确的是( )

A、 $x_{1} + x_{2} < 0$ B、 $4 < x_{2} < 5$ C、 $b^{2} - 4 a c < 0$ D、ab>0

查看解析
20、已知二次函数 $y = x^{2} + m x + m^{2} - 3 ($ 1为常数，且m>0)的图象过点 P(2，4).

(1)、求m 的值.

(2)、试判断二次函数 $y = x^{2} + m x + m^{2} - 3$ 的图象与x 轴交点的个数，并说明理由.

查看解析

上一页 290 291 292 293 294 下一页跳转

x	…	-1	-0.5	0	0.5	1	1.5	2	2.5	3	…
y	…	3	m	0	0.75	1	0.75	0	1.25	3	…